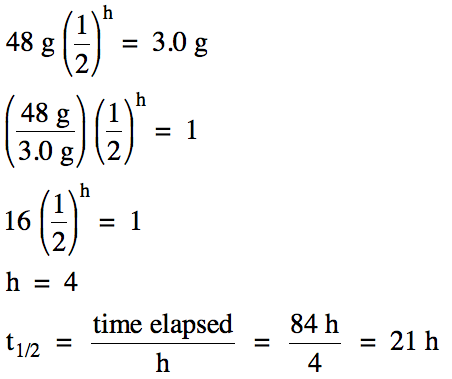Chapter 19: Nuclear Chemistry
Section 19-1: Balancing Nuclear Equations
Section 19-2: Nuclear Kinetics and Half-Life
Chapter 19 Practice Exercises and Review Quizzes
Section 19-1: Balancing Nuclear Equations
During a nuclear reaction, the
nuclei of the isotopes involved will undergo a change in composition. Each particle involved in a nuclear
reaction will be represented as follows, where Z is the atomic number and A is
the mass number:
When a nuclear reaction is
balanced, the sum of the Z values for the reactants must equal the sum of the Z
values for the products. Likewise,
the sum of the A values for the reactants must equal the sum of the A values
for the products. Note that
charges are typically omitted when nuclear reactions are written.
Types of radioactive decay include:
A. Alpha decay (or alpha emission)
= nucleus of an isotope X emits a helium-4 nucleus to produce a new isotope
Y. The equation is balanced as
follows:
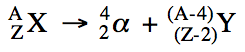
B. Beta decay (or beta emission) =
nucleus of an isotope X emits a particle equivalent to an electron to produce a
new isotope Y. The equation is
balanced as follows:
C. Positron decay (or positron
emission) = nucleus of an isotope X emits a particle equivalent to an electron,
but with a positive charge, to produce a new isotope Y. The equation is balanced as follows:
D. Electron capture = electron from
an inner orbital is absorbed into the nucleus of isotope X to produce a new
isotope Y. The equation is
balanced as follows:
In each case above, the identity of
the isotope Y can be determined by matching the atomic number of Y with an
element on the periodic table:
Sample Exercise 19A:
Write balanced equations for the
following nuclear reactions:
a. Uranium-235 decays by alpha
emission.
b. Rubidium-87 decays by beta emission.
c. Potassium-38 decays by positron
emission.
d. Iron-55 decays by electron
capture.
Solution:
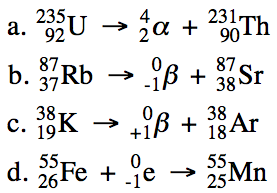
A nuclear reaction may also be
initiated by bombarding a sample of an isotope with particles such as neutrons
or protons in order to produce a new isotope. Other particles may be produced in the process as well. The symbols for a neutron and a proton
are as follows:
Sample Exercise 19B:
Neutron bombardment of nitrogen-14
produces a proton and a new isotope.
Write a balanced equation for this nuclear reaction.
Solution:
Section 19-2: Nuclear Kinetics and Half-Life
The half-life (t1/2) of
a radioactive isotope is the time required for the isotope to decay to half its
initial quantity. Given the
initial quantity (Qi)
of the isotope in any unit (such as grams, moles, or number of atoms), the
final quantity (Qf) can be calculated as
follows:
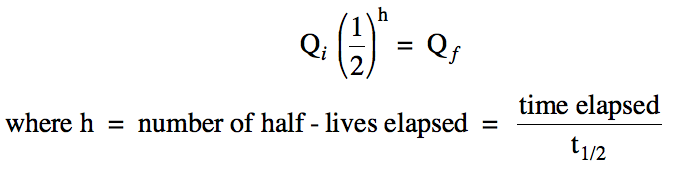
Sample Exercise 19C:
The half-life of bromine-80 is 18
minutes. What mass of bromine-80
will remain if a 96 gram sample decays for 72 minutes?
Solution:
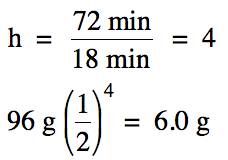
Sample Exercise 19D:
The half-life of potassium-40 is
1.25 x 109 years. How
much time is required for a 4.48 mol sample of
potassium-40 to decay to 0.0700 mol?
Solution:
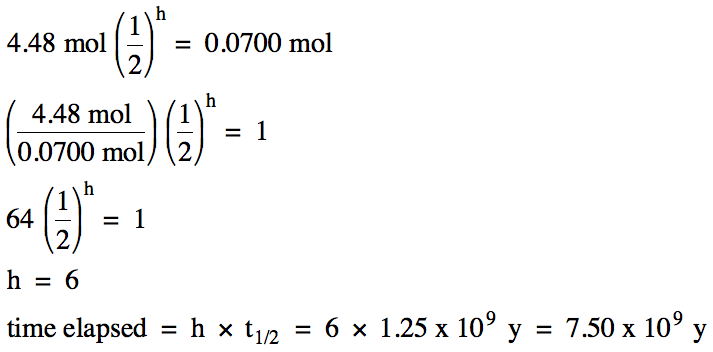
Sample Exercise 19E:
A sample of radon-222 containing
6.54 x 1025 atoms requires 26.7 days to decay to 5.11 x 1023
atoms. Calculate the half-life of
radon-222.
Solution:
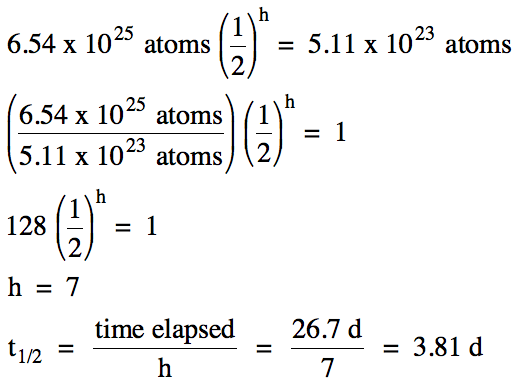
Chapter 19 Practice Exercises and Review Quizzes:
19-1) Write balanced equations for
the following nuclear reactions:
a. Lead-196 decays by electron
capture.
b. Phosphorus-28 decays by positron
emission.
c. Radium-226 decays by alpha
emission.
d. Zinc-73 decays by beta
emission.
Click for Solution
19-1)
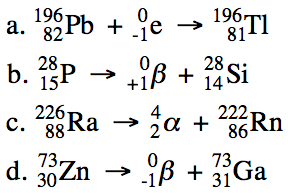
19-2) Proton bombardment of
magnesium-26 produces an alpha particle and a new isotope. Write a balanced equation for this
nuclear reaction.
Click for Solution
19-2)
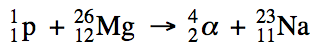
19-3) The
half-life of oxygen-13 is 0.00870 seconds. How many moles of oxygen-13 will remain if a 38.4 mol sample
decays for 0.0696 seconds?
Click for Solution
19-3)
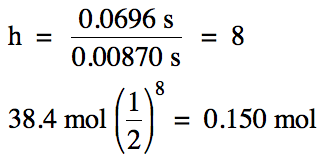
19-4) The
half-life of iodine-131 is 8.04 days.
How much time is required for a sample containing 6.56 x 1023
iodine-131 atoms to decay to 8.20 x 1022 atoms?
Click for Solution
19-4)
19-5) A 48
gram sample of magnesium-28 requires 84 hours to decay to 3.0 grams. Calculate the half-life of
magnesium-28.
Click for Solution
19-5)
Click for Review Quiz 1 Answers
Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License
Contact: kcardozo@andover.edu