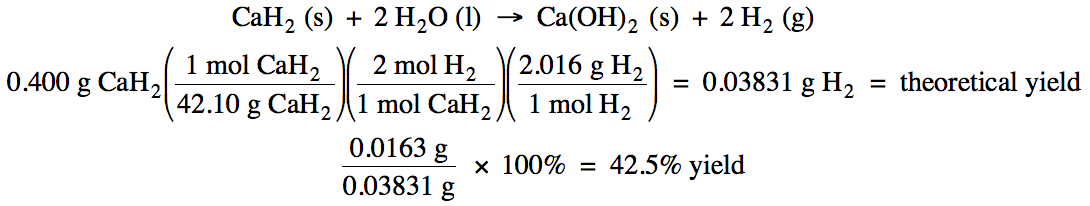Chapter 4: Balancing Chemical Equations and Stoichiometry

Section 4-1: Balancing Chemical Equations and States of Matter

Section 4-2: Mole Ratios and Stoichiometry

Chapter 4 Practice Exercises and Review Quizzes

Section 4-1: Balancing Chemical Equations and States of Matter

In a balanced chemical equation, the number of atoms of a particular element among the reactants on the left side of the arrow will be equal to the number of atoms of that same element among the products on the right side of the arrow. To balance a chemical equation, you may only change the coefficients that are written before each reactant and product. However, you may NOT change the subscripts in any chemical formulas as that would change the identities of the substances involved in the reaction. The problem below demonstrates key reasoning that may be utilized when balancing chemical equations:

Sample Exercise 4A:

Balance the following chemical equations using the smallest possible whole-number coefficients:

(a) P₄ + Cl₂ → PCl₃

(b) C₃H₇OH + O₂ → CO₂ + H₂O

Solution:

(a) Since there are 4 P atoms on the left but only 1 P atom on the right originally, we start by placing a coefficient of 4 in front of the PCl₃ so that there will be 4 P atoms on both sides:

P₄ + Cl₂ → 4 PCl₃

Because there are now 12 Cl atoms on the right (coefficient of 4 x subscript of 3 = 12) but only 2 Cl atoms on the left, we then place a coefficient of 6 in front of the Cl₂ so that there will be 12 Cl atoms on both sides:

Final Balanced Equation: P₄ + 6 Cl₂ → 4 PCl₃

(b) It is wise to begin by balancing those elements that only appear in one substance on the left and one substance on the right. Thus, we will balance the C and H atoms first but wait to balance the O atoms as they appear in more than one substance on both sides of the equation.

Since there are 3 C atoms on the left but only 1 C atom on the right originally, we start by placing a coefficient of 3 in front of the CO₂ so that there will be 3 C atoms on both sides:

C₃H₇OH + O₂ → 3 CO₂ + H₂O

Since there are 8 H atoms on the left but only 2 H atoms on the right, we then place a coefficient of 4 in front of the H₂O so that there will be 8 H atoms on both sides:

C₃H₇OH + O₂ → 3 CO₂ + 4 H₂O

At this point, there are 10 O atoms on the right. Since there is already 1 O atom in the C₃H₇OH on the left, we will need to change the coefficient in front of the O₂ in order to add 9 more O atoms. We can temporarily balance the equation by using a fraction in front of the O₂:

C₃H₇OH + 9/2 O₂ → 3 CO₂ + 4 H₂O

Although it is acceptable in certain situations to use fractions to balance a chemical equation, we were asked in this case to use the smallest possible whole-numbers, so we then multiply all coefficients in the equation above by 2 to eliminate the fraction while keeping the equation balanced with 6 C atoms, 16 H atoms, and 20 O atoms on both sides:

Final Balanced Equation: 2 C₃H₇OH + 9 O₂ → 6 CO₂ + 8 H₂O

Throughout this textbook, we may also indicate the state of matter of each reactant and product in a chemical equation as follows:

State of Matter	Abbreviation
Gas	(g)
Liquid	(l)
Solid	(s)
Aqueous (Dissolved in Water)	(aq)

Section 4-2: Mole Ratios and Stoichiometry

Stoichiometry is essentially the study of the quantities of substances in a chemical reaction. Once a chemical equation has been balanced, we will then know the ratios of the moles of all reactants and products involved in the reaction. For example, consider the second reaction that we balanced in the previous section:

2 C₃H₇OH + 9 O₂ → 6 CO₂ + 8 H₂O

Based on this balanced equation, the reactants react and the products are formed according to the following ratios:

2 mol C₃H₇OH: 9 mol O₂: 6 mol CO₂: 8 mol H₂O

Therefore, if we know the moles of any reactant or product involved in the reaction, we can find the unknown moles of any other reactant or product using dimensional analysis and the mole ratios above. For example, if 12 moles of C₃H₇OH react, we can find the moles of O₂ that react and the moles of CO₂ formed as follows:

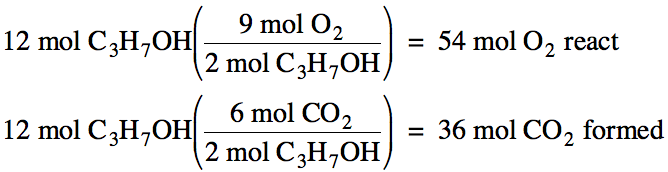
Although the mole ratio will be a central step in each stoichiometry problem, you may first need to convert from another unit to moles of the known reactant or product and then end by converting moles of the unknown reactant or product to another unit:

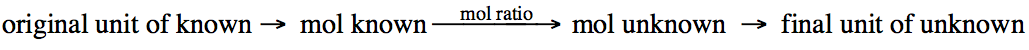
The following problem will demonstrate a common type of stoichiometry problem where both the original and final units are grams:

Sample Exercise 4B:

Given the unbalanced equation below, what mass of C₂H₅SH must react in order to produce 0.030 grams of water?

C₂H₅SH + O₂ → CO₂ + H₂O + SO₂

Solution:

First, balance the equation:

2 C₂H₅SH + 9 O₂ → 4 CO₂ + 6 H₂O + 2 SO₂

Next, convert the known mass of water to moles, then use a mole ratio to convert to the unknown moles of C₂H₅SH, and finally convert to grams of C₂H₅SH:

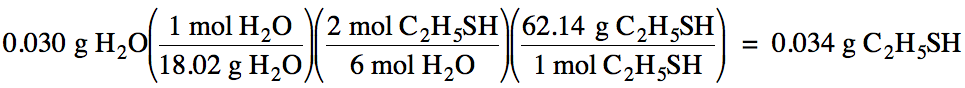
Section 4-3: Limiting Reagents

When two reactants are mixed to initiate a chemical reaction, one of the reactants may be used up completely while some of the other reactant may remain after the reaction is complete. The reactant that is used up completely is called the limiting reagent (or limiting reactant). We can use the initial amount of the limiting reagent and stoichiometry to determine the maximum amount of any product that can form in the reaction. The reactant that still remains after the reaction is complete is known as the excess reagent (or excess reactant), and we can calculate the amount of the excess reagent that remains using stoichiometry and subtraction. The following problem demonstrates how to identify the limiting reagent as well as how to calculate the maximum amount of product that can form and the amount of the excess reagent that remains:

Sample Exercise 4C:

Given the unbalanced equation below, if 31.6 grams of CS₂ is mixed with 17.0 grams of NaOH:

(a) Which is the limiting reagent?

(b) What maximum mass of Na₂CS₃ can form?

CS₂ + NaOH → Na₂CS₃ + Na₂CO₃ + H₂O

Solution:

First, balance the equation:

3 CS₂ + 6 NaOH → 2 Na₂CS₃ + Na₂CO₃ + 3 H₂O

Next, read through the entire problem to determine which product is being investigated. In this case, we are trying to find the mass of Na₂CS₃. As such, use stoichiometry to calculate which reactant can produce a lower mass of Na₂CS₃. The reactant that can produce less Na₂CS₃ is the limiting reagent, and the mass of Na₂CS₃ calculated from the limiting reagent will be your answer to (b).

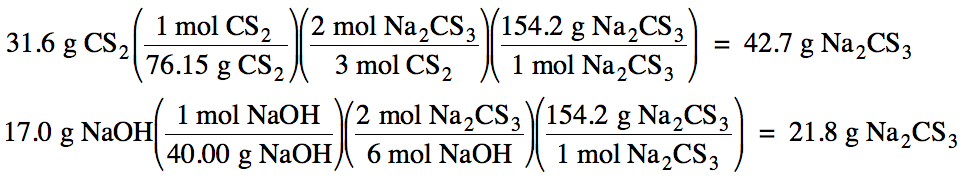
(a) NaOH produces less Na₂CS₃, so NaOH is the limiting reagent.

(b) 21.8 g Na₂CS₃ maximum can form.

(c) Use the mass of Na₂CS₃ that can form from the limiting reagent and stoichiometry to calculate the mass of the excess reagent, CS₂, used up in the reaction:

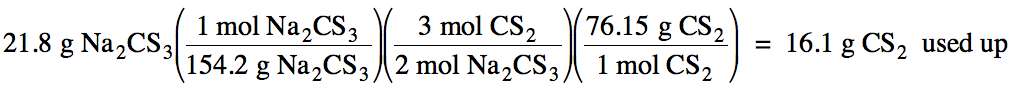
Finally, subtract the mass of CS₂ used up from the initial mass of CS₂ to calculate the excess mass of CS₂ remaining after the reaction is complete:

31.6 g – 16.1 g = 15.5 g CS₂ excess

Section 4-4: Percent Yield

The amount of a product calculated using stoichiometry is known as the theoretical yield and represents the maximum amount of the product that can form. However, for a variety of reasons, an amount less than the theoretical yield of the product may actually be collected in the lab. This amount is known as the actual yield. The percent yield of a reaction gives an indication of how close the actual yield is to the theoretical yield:

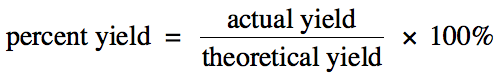
Note that any unit can be used to calculate the percent yield.

Sample Exercise 4D:

Given the unbalanced equation below, if 18 grams of solid copper reacts with an excess of aqueous AgNO₃ and then 48 grams of solid silver is actually collected, what is the percent yield of the reaction?

Cu (s) + AgNO₃ (aq) → Cu(NO₃)₂ (aq) + Ag (s)

Solution:

First, balance the equation:

Cu (s) + 2 AgNO₃ (aq) → Cu(NO₃)₂ (aq) + 2 Ag (s)

Next, use the mass of copper and stoichiometry to calculate the theoretical yield of silver in grams since the actual yield of silver given in the problem is in grams, then divide the actual yield by the theoretical yield to obtain the percent yield:

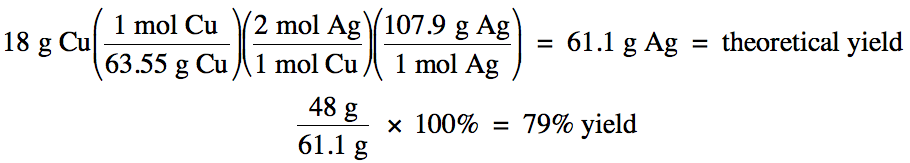
Chapter 4 Practice Exercises and Review Quizzes:

4-1) Balance the following chemical equations using the smallest possible whole-number coefficients:

(a) N₂ + H₂ → NH₃

(b) C₅H₁₁OH + O₂ → CO₂ + H₂O

Click for Solution

4-1) (a)

N₂ + H₂ → 2 NH₃

Final Balanced Equation: N₂ + 3 H₂ → 2 NH₃

(b)

C₅H₁₁OH + O₂ → 5 CO₂ + H₂O

C₅H₁₁OH + O₂ → 5 CO₂ + 6 H₂O

C₅H₁₁OH + 15/2 O₂ → 5 CO₂ + 6 H₂O

Final Balanced Equation: 2 C₅H₁₁OH + 15 O₂ → 10 CO₂ + 12 H₂O

4-2) Given the unbalanced equation below, if 0.970 kilograms of solid KClO₃ react, how many grams of oxygen gas will be produced?

KClO₃ (s) → KCl (s) + O₂ (g)

Click for Solution

4-2)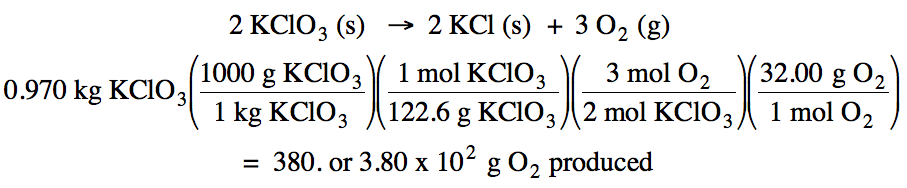

4-3) Given the unbalanced equation below, if 2.24 grams of HF is mixed with 9.93 grams of CCl₄:

(a) Which is the limiting reagent?

(b) What maximum mass of CCl₂F₂ can form?

HF + CCl₄ → HCl + CCl₂F₂

Click for Solution

4-3)

2 HF + CCl₄ → 2 HCl + CCl₂F₂

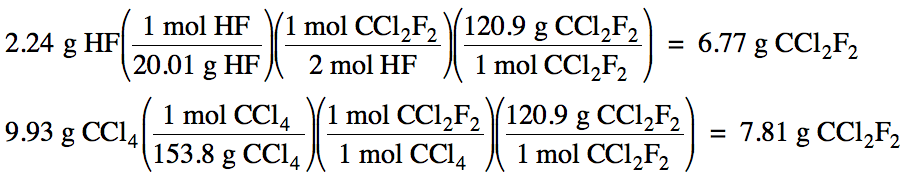
(a) HF produces less CCl₂F₂, so HF is the limiting reagent.

(b) 6.77 g CCl₂F₂ maximum can form.

(c)

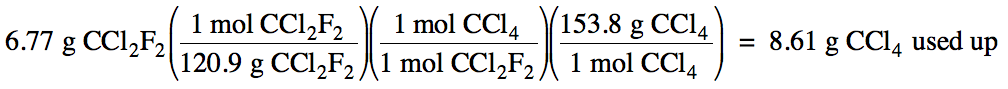
9.93 g - 8.61 g = 1.32 g CCl₄ excess

4-4) Given the unbalanced equation below, if 0.400 grams of solid CaH₂ reacts with an excess of water and then 0.0163 grams of hydrogen gas is actually collected, what is the percent yield of the reaction?

CaH₂ (s) + H₂O (l) → Ca(OH)₂ (s) + H₂ (g)

Click for Solution

4-4)

Click for Review Quiz 1

Click for Review Quiz 1 Answers