Chapter 14: Thermodynamics
Section 14-1: Predicting the Sign of the Entropy Change, ΔS
Section 14-2: Calculating ΔS° Using Standard Entropies, S°
Section 14-3: The Second Law of Thermodynamics and Gibbs Free Energy Change, ΔG
Section 14-4: The Effect of Temperature on ΔG and the Spontaneity of Reactions
Section 14-5: Calculating ΔG° from Standard Gibbs Free Energies of Formation, ΔGf°
Chapter 14 Practice Exercises and Review Quizzes
Section 14-1: Predicting the Sign of the Entropy
Change, ΔS
Whereas thermochemistry focuses primarily on the heat involved in chemical reactions, thermodynamics explores the role of energy more broadly. Entropy (S) is essentially an
indication of the level of disorder or chaos in a given system. The following processes generally occur
with an increase in entropy and, thus, a positive entropy change (ΔS):
1. The temperature of a substance
increases.
2. A solid is converted to a
liquid, solution, or gas (sublimation).
3. A liquid is converted to a gas.
4. A chemical reaction in which the
number of moles of gas increases (the sum of coefficients of gases among the
products on the right side is larger than the sum of coefficients of gases
among the reactants on the left side).
If the number of moles of gas does not change during a chemical
reaction, more information is generally needed to determine the sign of ΔS.
The
following processes generally occur with a decrease in entropy and, thus, a
negative ΔS:
1. The temperature of a substance
decreases.
2. A solid is formed from a liquid,
solution, or gas.
3. A gas is converted to a liquid.
4. A chemical reaction in which the
number of moles of gas decreases.
Sample Exercise 14A:
Predict the sign of ΔS for each
process:
(a) Water cools from 35°C to 25°C.
(b) Liquid ethanol freezes.
(c) Solid iodine dissolves in
carbon disulfide.
(d) 3 S (s) + 2 H2O (g) → SO2 (g) + 2 H2S
(g)
(e) Bromine vapor condenses.
(f) CO (g) + H2O (g) → CO2 (g) + H2
(g)
Solution:
(a) Temperature decreases, so ΔS
< 0.
(b) Liquid to solid, so ΔS < 0.
(c) Solid to solution, so ΔS >
0.
(d)
Although the total moles decrease (3 + 2 → 1 + 2),
the moles of gas increase (2 → 1 + 2). Therefore, ΔS > 0.
(e) Gas to liquid, so ΔS < 0.
(f) The moles of gas are unchanged
(1 + 1 → 1 + 1), so
more information is needed to determine the sign of ΔS.
Section 14-2: Calculating ΔS° Using Standard
Entropies, S°
We can calculate the standard
entropy change, ΔS°, for a reaction in the unit J/mol•K
using the standard entropies of the reactants and products as follows:

Sample Exercise 14B:
Predict the sign of ΔS° and then
calculate the value of ΔS° for the reaction N2 (g) + 3 F2
(g) → 2 NF3
(g) using the following information:
Solution:
ΔS° is expected to be negative
because the moles of gas decrease during the reaction (1 + 3 → 2).
ΔS° =
[2(261) - 1(192) - 3(203)] J/mol•K = -279 J/mol•K
Section 14-3: The Second Law of Thermodynamics and
Gibbs Free Energy Change, ΔG
A spontaneous process is one that
will continue to progress without outside intervention. According to the Second Law of Thermodynamics, the entropy of the universe must
increase as a result of a spontaneous process and, therefore, the entropy
change of the universe must be positive as a result of a spontaneous
process. For a chemical reaction,
we can consider the entropy change of the universe to be the sum of the entropy
change of the reaction plus the entropy change of the surroundings, which
includes everything but the reaction particles. Therefore, the Second Law of Thermodynamics can be expressed
for chemical reactions as follows:
spontaneous reaction:
ΔSuniverse = ΔSrxn
+ ΔSsurroundings > 0
ΔSsurroundings
is related to ΔHrxn and the Kelvin temperature as
follows: ΔSsurroundings
= -ΔHrxn/T. If we substitute for ΔSsurroundings
in the equation above, we obtain:
spontaneous reaction:
ΔSrxn - ΔHrxn/T
> 0
If we multiply both sides of the
equation by (-T), we obtain:
spontaneous reaction:
ΔHrxn – TΔSrxn
< 0
The quantity ΔHrxn
– TΔSrxn is known as the Gibbs free
energy change (or Gibbs energy change), ΔGrxn. Therefore, ΔGrxn
will be negative for a spontaneous reaction:
spontaneous reaction:
ΔGrxn = ΔHrxn
– TΔSrxn < 0
Note that if ΔGrxn
and ΔHrxn are expressed in kJ/mol, ΔSrxn must first be converted from J/mol•K to kJ/mol•K before using
the equation above.
Sample Exercise 14C:
For a certain reaction at 75°C, ΔH
= 118 kJ/mol and ΔS = 175 J/mol•K. Calculate ΔG for the reaction at 75°C
and determine if the reaction is spontaneous at this temperature.
Solution:

Since ΔG
> 0, the reaction is nonspontaneous at 75°C.
Section 14-4: The Effect of Temperature on ΔG and the
Spontaneity of Reactions
Given that the sign of the Kelvin
temperature cannot be negative, we see mathematically that:
1. A reaction with ΔH < 0 and ΔS > 0 will have ΔG = ΔH – TΔS < 0 at all temperatures. Therefore, the reaction will be spontaneous at all temperatures. Since both the negative sign of ΔH and the positive sign of ΔS lead to the reaction being favorable, the reaction is both enthalpy and entropy driven.
2. A reaction with ΔH > 0 and ΔS
< 0 will have ΔG = ΔH – TΔS > 0 at all temperatures. Therefore, the reaction will be nonspontaneous at all temperatures.
3. A reaction with ΔH > 0 and ΔS
> 0 will have ΔG = ΔH – TΔS < 0 only at relatively high
temperatures. Therefore, the
reaction will only be spontaneous at relatively high temperatures. Since only the positive sign of ΔS (but not the positive sign of ΔH) leads to the reaction being favorable, the reaction is entropy driven.
4. A reaction with ΔH < 0 and ΔS < 0 will have ΔG = ΔH – TΔS < 0 only at relatively low temperatures. Therefore, the reaction will only be spontaneous at relatively low temperatures. Since only the negative sign of ΔH (but not the negative sign of ΔS) leads to the reaction being favorable, the reaction is enthalpy driven.
The discussion above is summarized
in the following table:
ΔH
|
ΔS
|
ΔG = ΔH – TΔS
|
Reaction is
|
(-)
|
(+)
|
(-) at all T
|
spontaneous at all T, both enthalpy and entropy driven
|
(+)
|
(-)
|
(+) at all T
|
nonspontaneous at all T
|
(+)
|
(+)
|
(-) at high T only
|
spontaneous at high T only, entropy driven |
(-)
|
(-)
|
(-) at low T only
|
spontaneous at low T only, enthalpy driven
|
Sample Exercise 14D:
Determine whether reactions with
the following ΔH and ΔS values will be spontaneous at all temperatures, nonspontaneous at all temperatures, spontaneous at high
temperatures only, or spontaneous at low temperatures only. Also indicate the driving force for each spontaneous reaction:
(a) ΔH = 42 kJ/mol, ΔS = 86 J/mol•K
(b) ΔH = -242 kJ/mol, ΔS = 357 J/mol•K
(c) ΔH = -124 kJ/mol, ΔS = -289 J/mol•K
(d) ΔH = 26 kJ/mol, ΔS = -33 J/mol•K
Solution:
(a) spontaneous at high T only, entropy driven
(b) spontaneous at all T, both enthalpy and entropy driven
(c) spontaneous at low T only, enthalpy driven
(d) nonspontaneous at all T
For reactions that are neither
spontaneous at all temperatures nor nonspontaneous at
all temperatures, we can estimate the cutoff temperature at which the reaction
changes from spontaneous to nonspontaneous by setting
ΔG equal to zero in the equation ΔG = ΔH – TΔS and then solving for the
temperature. Note that the
calculated cutoff temperature is only an estimate because the ΔH and ΔS values
used in the calculation may change appreciably as the reaction temperature
increases or decreases.
Sample Exercise 14E:
For a reaction with ΔH = -77.1
kJ/mol and ΔS = -121 J/mol•K, estimate the cutoff
temperature in °C at which the reaction changes from spontaneous to nonspontaneous and also specify if the reaction is
spontaneous above or below this cutoff temperature.
Solution:

Therefore, the cutoff temperature
in °C is 637 K – 273 = 364°C.
Since both ΔH and ΔS are negative, the reaction will only be spontaneous
below 364°C.
Section 14-5: Calculating ΔG° from Standard Gibbs
Free Energies of Formation, ΔGf°
We can calculate the standard Gibbs
free energy change, ΔG°, for a reaction directly using the standard Gibbs free
energies of formation of the reactants and products as follows:
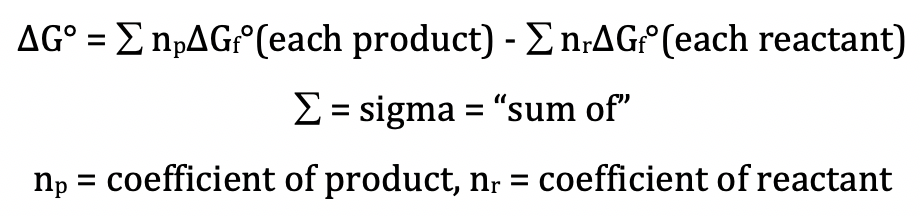
Note that ΔGf° = 0 kJ/mol for all elements
in their standard states.
Sample Exercise 14F:
Calculate ΔG° for the reaction 2 H2S
(g) + 3 O2 (g) → 2 H2O
(l) + 2 SO2 (g) using the following information:
Solution:
ΔGf° = 0 kJ/mol for the standard state element O2
(g), so ΔG° = [2(-237.2) + 2(-300.2) - 2(-33.6) - 3(0)] kJ/mol = -1007.4 kJ/mol
Chapter 14 Practice Exercises and Review Quizzes:
14-1) Predict
the sign of ΔS for each process:
(a) Ice melts.
(b) 2 C8H18
(l) + 25 O2 (g) → 16 CO2
(g) + 18 H2O (l)
(c) Helium gas is heated from room
temperature to 200°C.
(d) Dry ice (solid carbon dioxide)
sublimes.
(e) Sodium chloride crystallizes
from a salt water solution.
(f) Liquid methanol evaporates.
Click for Solution
14-1)
(a) Solid to liquid, so ΔS > 0.
(b) Although the total moles
increase (2 + 25 → 16 + 18),
the moles of gas decrease (25 → 16). Therefore, ΔS < 0.
(c) Temperature increases, so ΔS
> 0.
(d) Solid to gas, so ΔS > 0.
(e) Solution to solid, so ΔS <
0.
(f) Liquid to gas, so ΔS > 0.
14-2) Predict the sign of ΔS° and then
calculate the value of ΔS° for the reaction CH4 (g) + 2 O2
(g) → CO2
(g) + 2 H2O (g) using the following information:
|
Substance |
S° (J/mol•K) |
|
CH4
(g) |
186.2 |
|
CO2
(g) |
213.6 |
|
H2O
(g) |
188.7 |
|
O2
(g) |
205.0 |
Click for Solution
14-2) The
sign of ΔS° is difficult to predict and likely close to zero because the moles
of gas are unchanged (1 + 2 → 1 +
2).
ΔS° =
[1(213.6) + 2(188.7) - 1(186.2) – 2(205.0) J/mol•K
= -5.2 J/mol•K
14-3) For
a certain reaction at 115°C, ΔH = -88 kJ/mol and ΔS = -170. J/mol•K.
Calculate ΔG for the reaction at 115°C and determine if the reaction is
spontaneous at this temperature.
Click for Solution
14-3)

Since ΔG
<0, the reaction is spontaneous at 115°C.
14-4) Determine whether reactions with
the following ΔH and ΔS values will be spontaneous at all temperatures, nonspontaneous at all temperatures, spontaneous at high
temperatures only, or spontaneous at low temperatures only. Also indicate the driving force for each spontaneous reaction:
(a) ΔH = 609 kJ/mol, ΔS = -322 J/mol•K
(b) ΔH = -92 kJ/mol, ΔS = -46 J/mol•K
(c) ΔH = 65 kJ/mol, ΔS = 73 J/mol•K
(d) ΔH = -402 kJ/mol, ΔS = 149 J/mol•K
Click for Solution
14-4)
(a) nonspontaneous at all T
(b) spontaneous
at low T only, enthalpy driven
(c) spontaneous
at high T only, entropy driven
(d) spontaneous
at all T, both enthalpy and entropy driven
14-5) For
a reaction with ΔH = 47.3 kJ/mol and ΔS = 120. J/mol•K,
estimate the cutoff temperature in °C at which the reaction changes from
spontaneous to nonspontaneous and also specify if the
reaction is spontaneous above or below this cutoff temperature.
Click for Solution
14-5)

Therefore, the cutoff temperature
in °C is 394 K – 273 = 121°C.
Since both ΔH and ΔS are positive, the reaction will only be spontaneous
above 121°C.
14-6)
Calculate ΔG° for the
reaction Fe3O4 (s) + 4H2 (g) → 3 Fe (s) + 4 H2O (g) using the following information:
|
Compound |
ΔGf° (kJ/mol) |
|
Fe3O4
(s) |
-1015 |
|
H2O
(g) |
-229 |
Click for Solution
14-6) ΔGf°
= 0 kJ/mol for the standard state elements H2 (g) and Fe (s), so ΔG°
= [3(0) + 4(-229) – 1(-1015) – 4(0)] kJ/mol = 99 kJ/mol
14-7) Given the reaction N2H4 (l) + 2 H2O2 (l) → N2 (g) + 4 H2O (g) ΔS° = 609 J/mol•K, use the information below to calculate S° for H2O2 (l):
Compound
|
S° (J/mol•K)
|
H2O
(g)
|
189
|
N2 (g)
|
192
|
N2H4 (l)
|
121
|
Click for Solution
14-7)
ΔS° = 609
J/mol•K = 1(192 J/mol•K) + 4(189 J/mol•K) – 1(121 J/mol•K) – 2(S°
for H2O2 (l))
S° for H2O2 (l) = 109 J/mol•K
14-8) Given the reaction Fe2O3 (s) + 3 CO (g) → 2 Fe (s) +
3 CO2 (g) ΔG° =
-29 kJ/mol, use the information below to calculate ΔGf°, for carbon
monoxide gas:
Compound
|
ΔGf° (kJ/mol)
|
CO2 (g)
|
-394
|
Fe2O3 (s)
|
-742
|
Click for Solution
ΔG° = -29
kJ/mol = 2(0 kJ/mol) + 3(-394 kJ/mol) – 1(-742 kJ/mol) – 3(ΔGf°
for CO (g))
ΔGf°
for CO (g) = -137 kJ/mol
