Chapter 19:  Chemical Kinetics

 

 

Section 19-1: Collision Theory and Factors That Increase Chemical Reaction Rates

Section 19-2: Reaction Energy Profiles (Reaction Progress Diagrams)

Section 19-3: Reaction Mechanisms

Section 19-4: Catalysis

Section 19-5:  Determining Reaction Order and Rate Law Using Method of Initial Rates

Section 19-6:  Determining Reaction Order and Rate Law Using Concentration Versus Time Data

Section 19-7:  Relationship Between Rate Law and Reaction Mechanism

Section 19-8:  The Arrhenius Equation - Effect of Temperature on Rate Constants

Chapter 19 Practice Exercises and Review Quizzes

 

 

 

 

Section 19-1:  Collision Theory and Factors That Increase Chemical Reaction Rates

Chemical kinetics focuses on the rates of chemical reactions.  Collision theory suggests that chemical reactions occur as a result of collisions between reactant molecules.  Therefore, the rates of chemical reactions will generally increase when the number of collisions between reactant molecules is increased by increasing the concentration of aqueous or gaseous reactants or increasing the surface area of solid reactants.

 

However, for a collision between reactant molecules to actually result in a reaction, the following requirements must also be met:

 

A. The reactant molecules must collide with the proper orientation or at the proper angle.

 

B. The total kinetic energy (energy of motion) of the reactant molecules must be equal to or greater than the required minimum energy, which is known as the activation energy and will be different for each different chemical reaction.  Therefore, the rates of chemical reactions will generally increase when the percentage of reactant molecules that possess the required activation energy is increased by increasing the temperature.

 

 

Section 19-2:  Reaction Energy Profiles (Reaction Progress Diagrams)

A reaction energy profile (or reaction progress diagram) traces the changes in energy that occur as reactants are transformed into products.  Reactant molecules that collide with the required activation energy are able to form a higher-energy temporary species known as the transition state (or activated complex) on the way to becoming product molecules.  The activation energy (E_a) is shown on a reaction energy profile as the difference in energy between the reactants and the transition state.  The difference in energy between the reactants and products is represented as ΔH on a reaction energy profile.  When the products have a lower energy than the reactants, the reaction is exothermic and energy is released during the overall reaction:

 

 

 

When the products have a higher energy than the reactants, the reaction is endothermic and energy is absorbed during the overall reaction:

 

 

 

 

Note that the rate of a chemical reaction will be higher when the required activation energy is lower, but the rate of a chemical reaction does not depend on ΔH. 

 

 

 

 

 

 

 

Section 19-3:  Reaction Mechanisms

 

A reaction mechanism depicts at the molecular level the actual series of elementary steps that occur during a chemical reaction and add up to give the overall balanced equation.  If the hypothetical reaction 2 A + B → C occurred in a single step, three reactant molecules would need to collide simultaneously.  Alternatively, it is possible that the reaction occurs via a two-step mechanism wherein two A molecules collide in a first step to form an intermediate (Int.), then the intermediate collides with a B molecule in a second step to form the product C:

 

Step 1:  A + A → Int.

Step 2:  Int. + B → C

 

Note that the intermediate is formed in one step but then consumed in the second step, so the intermediate will not appear in the overall balanced equation:

 

Sample Exercise 19A:

 

The following mechanism has been proposed for a reaction:

 

Step 1:  NO + NO → N₂O₂

Step 2:  N₂O₂ + O₂ → 2 NO₂

 

Identify the intermediate and write the overall balanced equation for the reaction.

 

Solution:

 

N₂O₂ is formed in the first step but then consumed in the second step, so N₂O₂ is the intermediate that cancels out of the overall balanced equation 2 NO + O₂ → 2 NO₂.

 

 

Section 19-4:  Catalysis

 

The addition of a catalyst to a reaction mixture allows the reaction to proceed via an alternate mechanism that is faster overall than the uncatalyzed mechanism.  For example, if the hypothetical uncatalyzed reaction A + B → D proceeds via a slow one-step mechanism, addition of a catalyst (Cat.) can increase the reaction rate by providing the following faster two-step mechanism:

 

 Step 1:  A + Cat. → Int.

Step 2:  Int. + B → D + Cat.

 

Note that the catalyst is consumed in the first step but then produced in the second step, so the catalyst will not appear in the overall balanced equation.  Also, a relatively small quantity of the catalyst must be added initially because each catalyst molecule produced in the second step can be used again as a reactant in the first step.

 

The alternate mechanism provided by a catalyst results in a lower-energy transition state and, therefore, a lower activation energy for the catalyzed reaction, as shown in the reaction energy profile below for an exothermic reaction (solid curve represents the uncatalyzed reaction): 

 

 

 

 

Note that ΔH is unaffected by the addition of a catalyst because the energies of both the reactants and the products are unchanged when a catalyst is added.

 

 

 

 

 

 

 

Section 19-5:  Determining Reaction Order and Rate Law Using Method of Initial Rates

 

The rate of a chemical reaction typically indicates a change in the concentration of a reactant or product during a certain period of time in units such as M•s^-1 or M•min^-1.  If we know the rate of a reaction in terms of one reactant or product, we can determine the rate of the reaction in terms of any other reactant or product using a mole ratio from the balanced equation as follows:

 

Sample Exercise 19B:

 

If the rate of disappearance of hydrogen gas in the reaction N₂ (g) + 3 H₂ (g) → 2 NH₃ (g) is found to be 0.018 M•s^-1, what is the rate of formation of NH₃ gas? 

 

Solution:

   

A rate law or rate equation expresses the relationship between reaction rate and the molarities of the reactants.  For a reaction of the type aA + bB → products, where a and b are coefficients, the rate law has the following form:

 

rate = k[A]^x[B]^y

 

Each particular reaction has its own unique rate constant k.  The exponent x is known as the order with respect to A, and the exponent y is known as the order with respect to B.  The sum of x and y is known as the overall reaction order.  Although the orders x and y may be equal to the coefficients a and b, these orders are often unequal to the coefficients and in some cases can be negative, zero, or fractional. 

 

The orders x and y and the value of the rate constant k can be determined experimentally using the method of initial rates.  A series of experiments are performed in which at least one of the initial reactant molarities are changed each time, and the initial reaction rate is measured for each experiment.  The data table is then utilized as follows:

 

1. For each separate experiment, the initial reactant molarities and initial rate are substituted into the rate law.

 

2. Two experiments are identified where only one of the initial reactant molarities are changed.  The rate laws for these two experiments are then divided to find the order with respect to one of the reactants.

 

3. The rate laws for a different combination of two experiments are divided to find the order with respect to the second reactant.

 

4. Once both orders have been determined, the initial reactant molarities and initial rate from any one of the experiments are substituted into the rate law to calculate the value of the rate constant k.

 

Sample Exercise 19C:

 

For the reaction 2 NO (g) + 2 H₂ (g) → N₂ (g) + 2 H₂O (g), the following data were collected:

 

 

Determine the overall order of the reaction, write the rate law, and calculate the value of k with units.

 

Solution:

 

 

Note that the initial reactant molarities and initial rate from Experiment 2 or Experiment 3 could also have been used to calculate the value of k. 

 

 

 

 

 

 

 

 

 

Section 19-6:  Determining Reaction Order and Rate Law Using Concentration Versus Time Data

 

For a reaction of the type aA → products, the rate law has the following form:  rate = k[A]^x .  For each different reaction order, we can use calculus to derive an equation known as an integrated rate law that allows us to calculate the molarity of A at different points in time (t) during the reaction.  Starting with the initial molarity of A at t = 0, [A]₀, the integrated rate law yields the molarity of A for any value of t, [A]_t. 

 

To determine reaction order, an alternative to the method of initial rates that requires only a single experiment involves monitoring the concentration of A over time during the reaction.  The concentration versus time data can then be analyzed to determine the reaction order as follows:

 

Zero-order reaction

 

rate law:  rate = k[A]⁰ = k

integrated rate law:  [A]_t = -kt + [A]₀

 

If the reaction is zero-order, a graph that plots [A]_t on the y-axis versus t on the x-axis will yield a straight line with slope = -k and y-intercept = [A]₀: 

 

 

First-order reaction

 

rate law:  rate = k[A]¹

integrated rate law:  ln[A]_t = -kt + ln[A]₀

 

If the reaction is first-order, a graph that plots ln[A]_t on the y-axis versus t on the x-axis will yield a straight line with slope = -k and y-intercept = ln[A]₀:

 

 

Note that any concentration of A below 1 M will yield a negative value for ln[A]_t.  Thus, data points may have a y-value below zero on the graph above.

 

Second-order reaction

 

rate law:  rate = k[A]²

integrated rate law:  1/[A]_t = kt + 1/[A]₀

 

If the reaction is second-order, a graph that plots 1/[A]_t on the y-axis versus t on the x-axis will yield a straight line with slope = +k and y-intercept = 1/[A]₀:

 

 

After the [A]_t versus t data are collected experimentally, the three graphs above of [A]_t versus t, ln[A]_t versus t, and 1/[A]_t versus t are plotted.  The graph on which the data points most closely fit a straight line indicates the reaction order as follows:

 

 

 

Sample Exercise 19D:

 

Concentration versus time data were collected for the reaction 2 H₂O₂ (aq) → O₂ (g) + 2 H₂O (l).  Graphs of [H₂O₂]_t v. t, ln[H₂O₂]_t v. t, and 1/[H₂O₂]_t v. t were plotted, and the data points on the graph of ln[H₂O₂]_t v. t were found to fit a straight line most closely.  Is the reaction zero-order, first-order, or second-order?

 

Solution:

 

Since the data points on the graph of ln[H₂O₂]_t v. t had the best straight line fit, the reaction is first-order.

 

 

 

Section 19-7:  Relationship Between Rate Law and Reaction Mechanism

 

For the reaction A + 2 B → C, consider the following proposed mechanism where k₁ is the rate constant for the first elementary step and k₂ is the rate constant for the second elementary step:

 

 

The rate of an elementary step in a reaction mechanism can be found by multiplying the rate constant for the step by the molarity of each reactant in the step raised to its coefficient.  The rate law for the overall reaction is essentially equal to the rate law for the slowest elementary step in the mechanism, which is referred to as the rate-determining (or rate-limiting) step.  Therefore, we can deduce a rate law for the overall reaction that is consistent with the proposed mechanism above as follows:

 

overall rate = rate of slow step = k₁[A]¹[B]¹

 

Sample Exercise 19E:

 

For the reaction CO + NO₂ → CO₂ + NO, consider the following proposed mechanism:

 

 

Deduce a rate law for the overall reaction that is consistent with the proposed mechanism above.

 

Solution:

 

overall rate = rate of slow step = k₁[NO₂]²

 

 

For the reaction A₂ + B₂ → 2 AB, consider the following proposed mechanism where k_-1 is the rate constant for the reverse reaction in the first equilibrium elementary step:

 

 

To deduce a rate law for the overall reaction that is consistent with the proposed mechanism above, we begin by writing the following:

 

overall rate = rate of slow step = k₂[A]²[B₂]¹

 

However, we must then eliminate the intermediate A from the rate law as follows:

 

 

Sample Exercise 19F:

 

For the reaction 2 H₂ + 2 NO → 2 H₂O + N₂, consider the following proposed mechanism:

 

 

Deduce a rate law for the overall reaction that is consistent with the proposed mechanism above.

 

Solution:

 

 

 

 

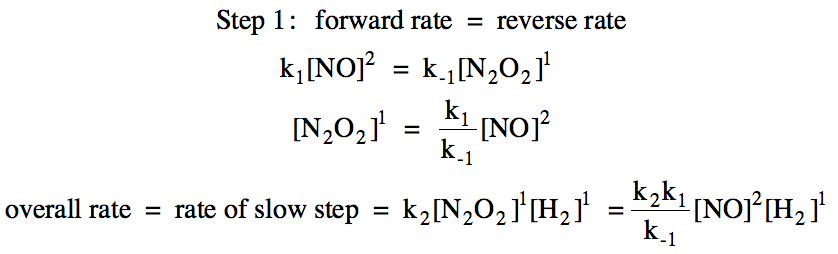
Section 19-8:  The Arrhenius Equation – Effect of Temperature on Rate Constants

The rate constant for a reaction will increase as the temperature increases.  If we know the rate constant for a reaction at one temperature as well as the activation energy, we can use the Arrhenius equation below (with T in K and R = 8.31 J/mol•K ) to calculate the rate constant at a second temperature:

 

 

Sample Exercise 19G:

The activation energy for a reaction is 77 kJ/mol.  If k = 2.9 x 10^-4 s^-1 at 25°C for the reaction, calculate k for the reaction at 45°C.

 

Solution:

 

 

 

 

Chapter 19 Practice Exercises and Review Quizzes:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Click for Review Quiz 1

Click for Review Quiz 1 Answers