Chapter 13: Thermochemistry

Section 13-1: Enthalpy of Reaction, ΔH

Section 13-2: Estimating ΔH Using Bond Energies

Section 13-3: Calculating ΔH Using Hess's Law

Section 13-4: Calculating ΔH° Using Standard Enthalpies of Formation, ΔH_f°

Section 13-5: Heat Transfer and the First Law of Thermodynamic

Section 13-6: Experiment - Determining the Specific Heat of a Metal Using Calorimetry

Section 13-7: Experiment - Determining ΔH Using Calorimetry

Section 13-8: ΔH for Changes of Physical State and Heating/Cooling Curves

Section 13-9: Experiment - Determining ΔH_fusion of Ice

Chapter 13 Practice Exercises and Review Quizzes

Section 13-1: Enthalpy of Reaction, ΔH

Thermochemistry is essentially the study of the heat released or absorbed by a reaction. A reaction that releases heat is said to be exothermic, while a reaction that absorbs heat is said to be endothermic. The heat released or absorbed by a reaction under constant pressure conditions is known as the enthalpy of reaction, ΔH. For an exothermic reaction, ΔH will be negative, while ΔH will be positive for an endothermic reaction. To express information about the heat of a reaction, the value of ΔH is typically written after the reaction in the unit kilojoules per mole as follows:

2 C₂H₆ (g) + 7 O₂ (g) → 6 H₂O(g) + 4 CO₂ (g) ΔH = -3119 kJ/mol

Since ΔH is negative in this case, we know that the reaction is exothermic and releases heat. We can use ΔH as a conversion factor in the form

(where x is the coefficient of the particular reactant or product being considered) to convert between the actual amount reacted or produced and the actual amount of heat released in a given reaction situation:

Sample Exercise 13A:

If 5.40 grams of ethane is burned according to the combustion equation shown above, how much heat will be released?

Solution:

Since we are considering the reactant ethane, which has a coefficient of 2 in the equation above, x = 2 in the conversion factor. We first convert the grams of ethane to moles and then use the conversion factor to convert to the amount of heat released:

If instead we know the actual amount of heat in kJ involved in a given reaction situation and we wish to convert to the amount reacted or produced, we first use the conversion factor with kJ in the denominator and mol in the numerator, and then we can convert moles to any desired unit:

Sample Exercise 13B:

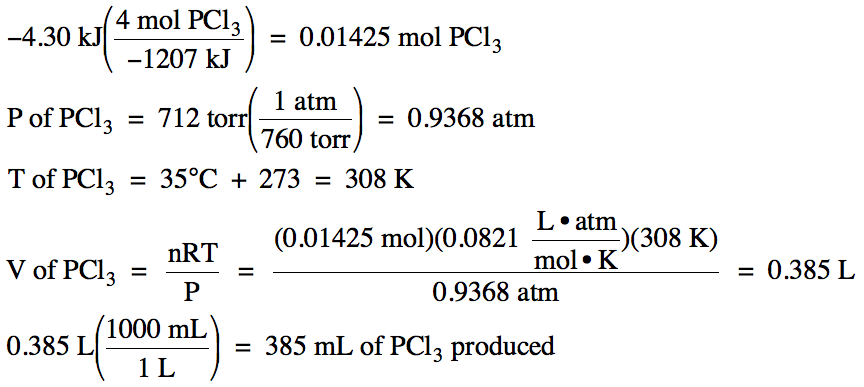
The formation of gaseous phosphorus trichloride is shown below:

P₄ (g) + 6 Cl₂ (g) → 4 PCl₃ (g) ΔH = -1207 kJ/mol

If 4.30 kJ of heat are released as the formation reaction above proceeds, how many milliliters of gaseous phosphorus trichloride, measured at 35°C and 712 torr, will be produced?

Solution:

The question specifies that heat is released, so we will need to make the given amount of heat negative and begin the calculation with -4.30 kJ. Since we are considering the product phosphorus trichloride, which has a coefficient of 4 in the equation above, x = 4 in the conversion factor. We first use the conversion factor to convert to moles of phosphorus trichloride, then we use the Ideal Gas Law to find the volume of phosphorus trichloride produced:

Section 13-2: Estimating ΔH Using Bond Energies

The following table shows a variety of different average bond energies:

Bond	Average Bond Energy (kJ/mol)
C-C	347
C=C	614
C≡C	839
C-H	414
C-O	360
C=O	745
F-F	157
F-N	272
N-N	163
N=N	418
N≡N	941
O-H	464
O-O	142
O=O	498

Breaking covalent bonds requires energy to be absorbed and is endothermic, whereas forming covalent bonds releases energy and is exothermic. For a chemical reaction in which all the reactants and products are gases, we can estimate ΔH by adding the positive energies absorbed to break all bonds in the reactant molecules to the negative energies released by the formation of all bonds in the product molecules, as demonstrated in the following problem:

Sample Exercise 13C:

Use average bond energies to estimate ΔH for the following reaction:

2 NF₃ (g) → N₂ (g) + 3 F₂ (g)

Solution:

First, draw a Lewis structure for each reactant and product molecule:

Then, being sure to take coefficients into account, add the positive energies absorbed to break all bonds in the reactant molecules to the negative energies released by the formation of all bonds in the product molecules to find ΔH:

ΔH (estimated) = (2x3)(N-F) – 1(N≡N) – 3(F-F)

= 6(272 kJ/mol) – 1(941 kJ/mol) – 3(157 kJ/mol) = 220 kJ/mol

Section 13-3: Calculating ΔH Using Hess's Law

When a reaction is reversed, the sign of ΔH changes:

When all the coefficients in a reaction are multiplied by the same number, ΔH is multiplied by that same number as well:

Hess's Law essentially states that the unknown ΔH for a reaction of interest can be determined by adding together the ΔH values from a series of two or more other reactions if the other reactions add up algebraically to the reaction of interest. For example, if we wish to find ΔH for the reaction A → C, we can add together the ΔH values from the following two reactions:

Reactions I and II add up algebraically to reaction III because an equal amount of B appears on both sides of the equation and, thus, can be canceled out.

In some cases, the given reactions with known ΔH values may not add up to the reaction of interest with an unknown ΔH. However, we may be able to first reverse one or more of the given reactions (and, thus, switch the sign of ΔH) and/or multiply all the coefficients of one or more of the given reactions (and, thus, multiply ΔH by that same number) before adding the reactions to find the unknown ΔH:

Sample Exercise 13D:

Calculate ΔH for the reaction C₂H₄ (g) + Cl₂ (g) → C₂H₄Cl₂ (l) using the following two reactions:

Solution:

Reactions I and II do not add up algebraically to the reaction of interest. However, if we reverse Reaction I and also multiply all the coefficients in Reaction I by ½ and then reverse Reaction II, the new reactions will add up algebraically to the reaction of interest because H₂O (l), 2 HCl (g), and ½ O₂ (g) will cancel out. Therefore, we can find the unknown ΔH by adding (-½ΔH_I) + (-ΔH_II):

Section 13-4: Calculating ΔH° Using Standard Enthalpies of Formation, ΔH_f°

The following table categorizes all elements into their standard states at 1 atm and 25°C, which is essentially room temperature:

Gases

Liquids

Solids

Cl₂, F₂, H₂, N₂, O₂

noble gases

Br₂, Hg

I₂

all other elements

C(graphite) is considered the standard state of solid carbon because it is more stable than the other allotrope, C(diamond).

When a formation reaction is written, 1 mole of a given compound is produced on the right side and each element present in the compound is shown separately in its standard state as a reactant on the left side:

Formation Reaction: standard state elements → 1 mol compound

To balance the equation while keeping 1 mole of the compound on the right side, it may be necessary to use fractions on the left side. For example, the formation reaction for solid ammonium iodide would be:

Sample Exercise 13E:

Write the balanced formation reaction, including physical states, for solid sucrose, C₁₂H₂₂O₁₁.

Solution:

ΔH for a formation reaction is known as the standard enthalpy of formation, ΔH_f°, and may be exothermic or endothermic. However, ΔH_f° = 0 kJ/mol for all elements in their standard states.

ΔH for a reaction carried out at 1 atm is known as the standard enthalpy of reaction, ΔH°. We can determine ΔH° for a reaction using known ΔH_f° values and Hess's Law. For example, consider the reaction aA + bB → cC + dD, where a and b are the coefficients of the reactants A and B, and c and d are the coefficients of the products C and D. Hess's Law suggests that we can determine ΔH° for this reaction by adding the following steps:

We can generalize this approach as follows:

Sample Exercise 13F:

Calculate ΔH° for the reaction 2 H₂S (g) + 3 O₂ (g) → 2 H₂O (l) + 2 SO₂ (g) using the following information:

Compound	ΔH_f° (kJ/mol)
H₂S (g)	-20.6
H₂O (l)	-285.8
SO₂ (g)	-296.8

Solution:

ΔH_f° = 0 kJ/mol for the standard state element O₂ (g), so ΔH° = [2(-285.8) + 2(-296.8) - 2(-20.6) - 3(0)] kJ/mol = -1124.0 kJ/mol

Section 13-5: Heat Transfer and the First Law of Thermodynamics

Calorimetry is essentially the measurement of heat in the laboratory. To calculate the quantity of heat (q) in joules gained (positive value) when a substance increases in temperature or lost (negative value) when a substance decreases in temperature, without a change in physical state, we multiply the mass (m) of the substance in grams by the specific heat (s) of the substance in J/g•°C and also by the temperature change of the substance (t_final – t _initial) in °C:

q = msΔt = ms(t_f – t_i)

Sample Exercise 13G:

The specific heat of copper metal is 0.385 J/g•°C. How much heat in joules and in kilojoules is lost when a 165 gram sample of copper metal is cooled from 98°C to 26°C?

Solution:

The First Law of Thermodynamics has been referred to as the Law of Conservation of Energy and essentially states that energy can neither be created nor destroyed. In calorimetry experiments, if one substance at a higher temperature is placed together with a second substance at a lower temperature in an insulated container that does not allow heat entry or exit, both substances will eventually reach the same final temperature. Furthermore, the First Law of Thermodynamics suggests that the amount of heat lost by the higher temperature substance will be exactly equal to the amount of heat gained by the lower temperature substance:

q_lost = -q_gained

Note that, although the magnitude of heat will be equal, q_lostis exothermic and will have a negative sign, whereas q_gained is endothermic and will have a positive sign.

Section 13-6: Experiment - Determining the Specific Heat of a Metal Using Calorimetry

The specific heat of water is known to be 4.18 J/g•°C. If a metal with unknown specific heat but known mass and initial temperature is mixed in an insulated calorimeter, such as a securely-covered Styrofoam coffee cup, with a known mass of water that also has a known initial temperature, the specific heat of the metal can be determined as follows:

Sample Exercise 13H:

In an insulated calorimeter, a 175 gram piece of aluminum metal originally at 304°C was added to 925 grams of water originally at 22°C. The final temperature of the aluminum-water mixture was 33°C. Determine the specific heat of aluminum.

Solution:

According to the First Law of Thermodynamics, the amount heat lost by the aluminum metal will be exactly equal to the amount of heat gained by the water (but opposite in sign):

q_Al_lost= -q_water_gained

We first calculate the amount of heat the water gained and then switch the sign to find the amount of heat the aluminum lost, after which we can calculate the specific heat of aluminum:

If we know the masses, specific heats, and initial temperatures of both the metal and the water, we can calculate the final temperature in the calorimeter after mixing, as demonstrated below in Practice Exercise 13-9.

Section 13-7: Experiment – Determining ΔH Using Calorimetry

When a solid ionic compound (salt) is dissolved in water, the cations and anions become separated from each other and are hydrated as water molecules surround the ions to create ion-dipole interactions. If this process is exothermic, the reaction particles will release heat into the surrounding mixed solution and increase the temperature of the solution. If this process is endothermic, the reaction particles will absorb heat from the surrounding mixed solution and decrease the temperature of the solution. We can determine the heat lost or gained by the reaction, q_rxn, by first calculating the heat lost or gained by the surrounding solution, q_soln, and then switching the sign:

q_rxn = -q_soln

After finding q_rxn and converting to kilojoules, we can divide by the moles of salt dissolved to find ΔH for the process in kJ/mol of salt dissolved:

Sample Exercise 13I:

In an insulated calorimeter, 2.6 grams of solid ammonium chloride at 23.4°C was dissolved in 35.9 grams of water also at 23.4°C, after which the final temperature of the mixed solution was 18.6°C. If the specific heat of the mixed solution was 3.94 J/g•°C, determine ΔH for the dissolving process NH₄Cl (s) → NH₄Cl (aq) in kJ/mol NH₄Cl.

Solution:

Since the temperature of the mixed solution decreased, the mixed solution lost heat and the reaction particles gained heat in an endothermic reaction with ΔH > 0:

q_rxn_gained= -q_soln_lost

We first calculate the amount of heat the mixed solution lost and then switch the sign to find the amount of heat the reaction particles gained, after which we can convert to kilojoules and divide by the moles of ammonium chloride to find ΔH for the dissolving process NH₄Cl (s) → NH₄Cl (aq):

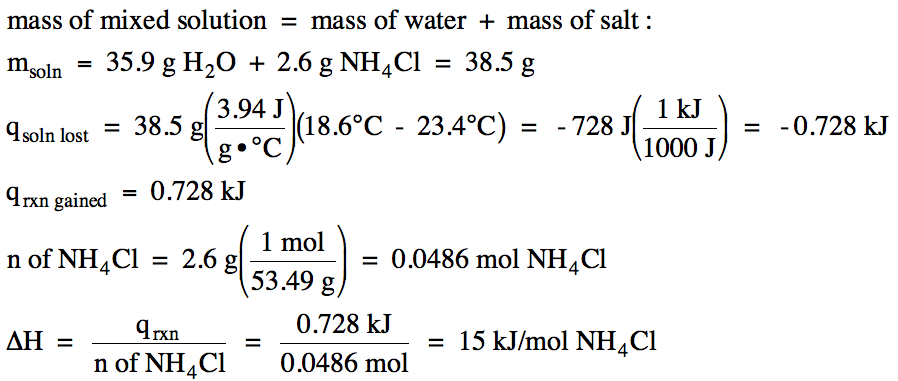
For neutralization reactions between an aqueous acid and an aqueous metal hydroxide, the process of determining ΔH by calorimetry is similar to that used for the dissolving of ionic salts, but the calculation typically differs in the following two ways:

1. Instead of masses being given, we may be given the volume of each solution being mixed, which we then can add to obtain the total volume of the mixed solution that absorbs heat from or releases heat into the reaction particles. If we are given the density of the mixed solutions, we can multiply by the volume of the mixed solutions to obtain the mass of the mixed solutions that is necessary in the calculation of q_soln.

2. In the final step, we divide q_rxn by the moles of a specified product formed in the reaction from the limiting reagent to obtain ΔH for the reaction.

Sample Exercise 13J:

In an insulated calorimeter, 45 mL of 1.0 M hydrochloric acid was mixed with 42 mL of 1.0 M sodium hydroxide, with both solutions originally at 19.4°C. The final temperature of the mixed solutions was 25.9°C. The density of the mixed solutions was 1.03 g/mL and the specific heat of the mixed solutions was 4.02 J/g•°C. Write a balanced molecular equation, including physical states, and determine ΔH for the neutralization reaction in kJ/mol of water formed.

Solution:

HCl (aq) + NaOH (aq) → H₂O (l) + NaCl (aq)

Since the temperature of the mixed solutions increased, the mixed solutions gained heat and the reaction particles lost heat in an exothermic reaction with ΔH < 0:

Section 13-8: ΔH for Changes of Physical State and Heating/Cooling Curves

Changes of physical state occur at a constant temperature. The endothermic change from solid to liquid is known as fusion and occurs at the melting point of the substance. To calculate the amount of heat absorbed when a given amount of a substance is melted, we multiply the moles melted by ΔH for the fusion process:

q = (n_melted)(ΔH_fusion)

If the same amount of the substance was frozen from a liquid to a solid rather than melted, the magnitude of heat involved would be exactly the same, but heat would be released in the exothermic process and q would be negative:

q = (n_frozen)(-ΔH_fusion)

The endothermic change from liquid to gas is known as vaporization and occurs at the boiling point of the substance. To calculate the amount of heat absorbed when a given amount of a substance is vaporized, we multiply the moles vaporized by ΔH for the vaporization process:

q = (n_vaporized)(ΔH_vaporization)

If the same amount of the substance was condensed from a gas to a liquid rather than vaporized, the magnitude of heat involved would be exactly the same, but heat would be released in the exothermic process and q would be negative:

q = (n_condensed)(-ΔH_vaporization)

A heating curve is a graph that depicts the changes in temperature and physical state that occur over time as heat is absorbed by a substance. The following sketch represents the general format of a heating curve for a substance originally below the melting point in the solid state being heated until it is a gas above the boiling point:

A cooling curve is a graph that depicts the changes in temperature and physical state that occur over time as heat is released by a substance. The following sketch represents the general format of a cooling curve for a substance originally above the boiling point in the gas state being cooled until it is a solid below the melting point (same temperature as freezing point):

Note that heating and cooling curves may encompass a less narrow temperature range and, therefore, may not include all five of the distinct segments shown in the two sketches above.

Sample Exercise 13K:

Consider the following data for H₂O:

Melting Point = 0.0°C

Boiling Point = 100.0°C

ΔH_fusion = 6.01 kJ/mol

ΔH_vaporization = 40.8 kJ/mol

Specific Heat of Ice = 2.03 J/g•°C

Specific Heat of Water = 4.18 J/g•°C

Specific Heat of Water Vapor = 1.99 J/g•°C

Sketch a heating curve that depicts ice at -25.0°C being heated until the temperature reaches 125.0°C and then calculate the total amount of heat in kilojoules absorbed when 175 grams of H₂O undergoes this process.

Solution:

We first calculate the amount of heat absorbed along each of the five distinct segments of the heating curve and then add the five heat values together to find the total heat absorbed:

q_total = 8.881 kJ + 58.37 kJ + 73.15 kJ + 396.2 kJ + 8.706 kJ = 545 kJ

Section 13-9: Experiment – Determining ΔH_fusion of Ice

Given the specific heats of ice and water in the previous problem, we can determine ΔH_fusion of ice in the laboratory by mixing in an insulated calorimeter a known mass of ice at a known original temperature below 0°C with a known mass of water at a known original temperature above 0°C. If we use enough water and/or a high enough original water temperature, all the ice will melt and the final temperature in the calorimeter will be above 0°C. The sketch below depicts the heating curve for the ice as its temperature rises to its melting point, the ice melts, and then the temperature of the melted ice rises to the final temperature. On the same sketch, the cooling curve for the water as it cools from its original temperature to the final temperature is also included:

The heat lost by the water as it cools to the final temperature will be equal in magnitude but opposite in sign to the total heat gained by the ice in the three segments of the heating curve above, which will allow us to determine ΔH_fusion of ice:

Sample Exercise 13L:

In an experiment to determine ΔH_fusion of ice, a student added 29.04 grams of ice originally at -15.1°C to 97.91 grams of water originally at 41.9°C in an insulated calorimeter. If the final temperature in the calorimeter was 13.2°C, calculate the experimentally determined ΔH_fusion of ice.

Solution:

The heating curve for the ice + cooling curve for the water is:

Chapter 13 Practice Exercises and Review Quizzes:

13-1) The decomposition of ammonia gas into nitrogen gas and hydrogen gas is endothermic:

2 NH₃ (g) → N₂ (g) + 3 H₂ (g) ΔH = 92 kJ/mol

If 762 mL of hydrogen gas, measured at 325°C and 792 mmHg, is formed in the reaction above, how much heat will be absorbed?

Click for Solution

13-1)

13-2) Consider the following reaction:

2 ZnS (s) + 3 O₂ (g) → 2 ZnO (s) + 2 SO₂ (g) ΔH = -878 kJ/mol

What mass of solid ZnS, in kilograms, must react according to the equation above in order for 5.41 x 10³ kJ of heat to be released?

Click for Solution

13-2) Heat is released = must start with -5.41 x 10³ kJ:

13-3) For the reaction 2 CH₃OH (g) + 3 O₂ (g) → 2 CO₂ (g) + 4 H₂O (g), estimate ΔH using average bond energies.

Click for Solution

13-3)

Lewis structures:

ΔH (estimated) = (2x3)(C-H) + (2x1)(C-O) + (2x1)(O-H) + (3x1)(O=O)

- (2x2)(C=O) - (4x2)(O-H)

= 6(414 kJ/mol) + 2(360 kJ/mol) + 2(464 kJ/mol) + 3(498 kJ/mol)

- 4(745 kJ/mol) – 8(464 kJ/mol) = -1066 kJ/mol

13-4) Calculate ΔH for the reaction 4 NH₃ (g) + 5 O₂ (g) → 4 NO (g) + 6 H₂O (l) using the following three reactions:

Click for Solution

13-4) Reactions I + II + III do not add up algebraically to the reaction of interest. However, if we multiply all the coefficients in Reaction I by 3, if we reverse Reaction II and multiply all coefficients in Reaction II by 2, and if we multiply all the coefficients in Reaction III by 2, the new reactions will add up algebraically to the reaction of interest because 2 N₂ (g) and 6 H₂ (g) will cancel out. Therefore, we can find the unknown ΔH by adding (3ΔH_I) + (-2ΔH_II) + (2ΔH_III):

13-5) Write the balanced formation reaction, including physical states, for liquid tribromomethane, CHBr₃.

Click for Solution

13-5)

13-6) Calculate ΔH° for the reaction 2 C₄H₁₀ (g) + 13 O₂ (g) → 10 H₂O(g) + 8 CO₂ (g) using the following information:

Compound	ΔH_f° (kJ/mol)
C₄H₁₀ (g)	-126.5
H₂O (g)	-241.8
CO₂ (g)	-393.5

Click for Solution

13-6) ΔH° = [10(-241.8) + 8(-393.5) - 2(-126.5) - 13(0)] kJ/mol = -5313.0 kJ/mol

13-7) The specific heat of lead metal is 0.130 J/g•°C. How much heat in joules and in kilojoules is gained when a 225 gram sample of lead metal is heated from 125°C to 241°C?

Click for Solution

13-7)

13-8) In an insulated calorimeter, a 225 gram piece of iron metal originally at 463°C was added to 845 grams of water originally at 27°C. The final temperature of the iron-water mixture was 39°C. Determine the specific heat of iron.

Click for Solution

13-8)

13-9) The specific heat of titanium metal is 0.54 J/g•°C. In an insulated calorimeter, a 265 gram piece of titanium metal originally at 285°C was added to 645 grams of water originally at 26°C. Determine the final temperature of the titanium-water mixture.

Click for Solution

13-9)

13-10) In an insulated calorimeter, 12.7 grams of solid calcium chloride at 21.4°C was dissolved in 129.1 grams of water also at 21.4°C, after which the final temperature of the mixed solution was 38.3°C. If the specific heat of the mixed solution was 3.89 J/g•°C, determine ΔH for the dissolving process CaCl₂ (s) → CaCl₂ (aq) in kJ/mol CaCl₂.

Click for Solution

13-10) Since the temperature of the mixed solution increased, the mixed solution gained heat and the reaction particles lost heat in an exothermic reaction with ΔH < 0:

13-11) In an insulated calorimeter, 85.6 mL of 2.55 M nitric acid was mixed with 94.3 mL of 2.51 M potassium hydroxide, with both solutions originally at 22.6°C. The final temperature of the mixed solutions was 39.1°C. The density of the mixed solutions was 1.04 g/mL and the specific heat of the mixed solutions was 3.98 J/g•°C. Write a balanced molecular equation, including physical states, and determine ΔH for the neutralization reaction in kJ/mol of water formed.

Click for Solution

13-11) HNO₃(aq) + KOH (aq) → H₂O (l) + KNO₃ (aq)

Since the temperature of the mixed solutions increased, the mixed solutions gained heat and the reaction particles lost heat in an exothermic reaction with ΔH < 0:

13-12) Consider the following data for ethanol, C₂H₅OH:

Melting Point = -114°C

Boiling Point = 78°C

ΔH_fusion = 5.0 kJ/mol

ΔH_vaporization = 42.6 kJ/mol

Specific Heat of Liquid Ethanol = 2.5 J/g•°C

Sketch a cooling curve that depicts ethanol vapor at 78°C being cooled until solid ethanol is formed at -114°C and then calculate the total amount of heat in kilojoules released when 55 grams of ethanol undergoes this process.

Click for Solution

13-12) In this case, there are only three distinct segments on the cooling curve because the ethanol vapor is already at the boiling point to start and the solid ethanol formed does not cool below the melting/freezing point:

We first calculate the amount of heat released along each of the three distinct segments of the cooling curve and then add the three heat values together to find the total heat released:

Click for Review Quiz 1

Click for Review Quiz 1 Answers