Chapter 1: Converting Units and Rounding Answers
Section 1-1: Converting Units Using Dimensional Analysis
Section 1-2: Significant Figures
Section 1-5: Experiment - Determining the Density of a Solid by Water Displacement
Chapter 1 Practice Exercises and Review Quizzes
Section 1-1: Converting Units Using Dimensional
Analysis
In life and in the chemistry
laboratory, you may find yourself taking a measurement in one particular unit,
but then needing to express your measurement in a different unit. The simple problem below will demonstrate
a systematic written approach to unit conversion known as Dimensional Analysis:
Sample Exercise 1A:
A penalty kick in soccer is taken
from a distance of 36 feet to the goal.
How many yards from the goal is this distance?
Solution:
We begin by noting the conversion
factor to be used:
1 yard (yd)
= 3 feet (ft)
We then multiply the original
measurement by the conversion factor expressed as a fraction in parentheses
with the desired unit in the numerator and the original unit in the
denominator:
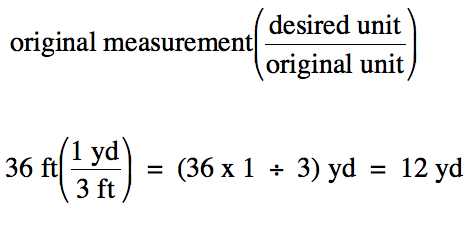
Note that the unit "ft" appears in
both the numerator and the denominator of the above calculation and, thus,
cancels out of the final answer.
Dimensional analysis may require
using two or more consecutive conversion factors, as shown in the following
problem:
Sample Exercise 1B:
A cross-country trip took a total
of 3600 minutes. How many days did
this trip take?
Solution:
We begin by outlining a multi-step
strategy to convert from the original to the desired unit:
minutes (min) → hours (hr)
→ days (d)
We then note the necessary
conversion factors in order and use them consecutively:
1 hr = 60 min
1 d = 24 hr
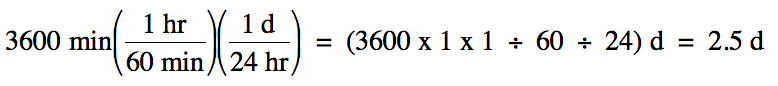
Note that it was not necessary to
stop and actually calculate the number of hours along the way to finding the
final answer in days.
Typical chemistry lab equipment
provides measurements with International System (SI) units that essentially
follow the metric system and utilize the following common prefixes to scale up
to larger units or down to smaller units:
|
Prefix |
Multiply Unit By |
|
kilo (k) |
1000 |
|
centi (c) |
1/100 |
|
milli (m) |
1/1000 |
Here are some common conversion
factors to help you convert between the customary U.S. units that you may
encounter in your daily life and SI units:
|
Measurement |
U.S. Unit |
SI Unit |
|
Distance/Length |
1 inch
(in) |
2.54
centimeters (cm) |
|
Energy |
1 calorie
(cal) |
4.18
joules (J) |
|
Mass |
1 pound
(lb) |
454 grams
(g) |
|
Volume |
1 gallon
(gal) |
3.79
liters (L) |
Section 1-2: Significant Figures
The number of significant figures (sig. fig.s) in a
measurement is essentially an indication of how precise the measurement
is. A measurement reported with
more sig. fig.s is considered to have less
uncertainty.
Use the following rules to
determine the number of sig. fig.s in a measurement:
1. All non-zero digits count as
sig. fig.s.
For example:
48 = 2 sig.
fig.s
25.7 = 3
sig. fig.s
2. All zeros between non-zero
digits count as sig. fig.s. For example:
102 = 3
sig. fig.s
7060.09 = 6
sig. fig.s
3. For measurements less than 1, all
zeros after the decimal point and to the right of the last non-zero digit count
as sig. fig.s, but all zeros to the left of the first
non-zero digit do not count as sig. fig.s. For example:
0.40
= 2 sig. fig.s
0.00080200
= 5 sig. fig.s
0.00009 = 1 sig. fig.
6.070 x 10-3
= 4 sig. fig.s
4. For measurements greater than or
equal to 1 with a decimal point shown, all zeros count as sig. fig.s. For
example:
1.00 = 3
sig. fig.s
220.0 = 4
sig. fig.s
56,000. = 5
sig. fig.s
5. For measurements greater than or
equal to 1 with no decimal point shown, the number of sig. fig.s
can be ambiguous. To avoid
ambiguity, it is best to use scientific notation in order to be clear about the
number of sig. fig.s intended. For example:
30,200 = ??? sig. fig.s
3.02 x 104
= 3 sig. fig.s
3.020 x 104
= 4 sig. fig.s
3.0200 x 104
= 5 sig. fig.s
Section 1-3: Rounding Answers
As we perform calculations
throughout this textbook, we will generally round answers according to the
following rules:
1. For problems where only 1 measurement
is given, round the final answer to the same number of sig. fig.s
as the original measurement.
Sample Exercise 1C:
Convert the following measurements:
(a) 0.030 miles (mi) to centimeters
(b) 20.0 milliliters to gallons
Solution:
(a) strategy:
mi → ft → in → cm
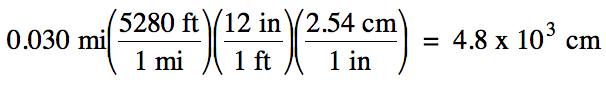
Since the original measurement 0.030
has 2 sig. fig.s, we should round the calculated
answer of 4828 down to 2 sig. fig.s using scientific
notation to avoid ambiguity.
(b) strategy: mL → L → gal
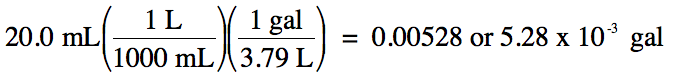
Since the original measurement 20.0
has 3 sig. fig.s, we must round up the calculated
answer of 0.005277 up to 3 sig. fig.s. In this case, whether or not to use
scientific notation is a matter of preference as long as the final answer has 3
sig. fig.s.
2. For problems that combine
addition or subtraction with multiplication or division, always perform all the
addition or subtraction steps first before proceeding to the multiplication or
division steps.
3. When two or more measurements
are added or subtracted, round the answer to the same number of decimal places
(NOT sig. fig.s!!!)
as the measurement with the fewest number of decimal places. For example:
9.8
(1 decimal place) + 0.35 (2 decimal places)
= {calculator says 10.15} = 10.2 (1 decimal place)
10.67
(2 decimal places) – 0.8700 (4 decimal places)
= 9.80
(2 decimal places)
4. When two or more measurements
are multiplied or divided, round the answer to the same number of sig. fig.s (NOT
decimal places!!!) as the measurement with the fewest number of sig. fig.s. For
example:
0.09000 (4 sig. fig.s) x 8.0 (2 sig. fig.s) x 12.0 (3 sig. fig.s)
= 0.060
(2 sig. fig.s)
Note that for longer problems
throughout the textbook, it is acceptable and often preferred to keep an extra
sig. fig. for each intermediate calculation as long as
the final answer is rounded to the proper number of sig. fig.s.
Section 1-4: Density
Density is the ratio of the mass of a substance to the volume of
space the substance occupies:
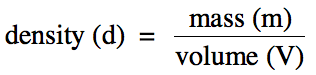
The densities of laboratory
chemicals are typically expressed in the SI unit g/cm3 or the
equivalent g/mL. (Note, however, that the density unit g/mL
is not used for solids.)
Sample Exercise 1D:
A 41.1 g piece of iron metal is
found to occupy a volume of 5.2 cm3. What is the density of the iron metal?
Solution:
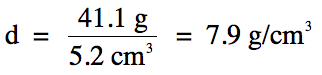
Note that since we are dividing
41.1 (3 sig. fig.s) by 5.2 (2 sig. fig.s), the final answer should be rounded to 2 sig. fig.s.
The density equation above can be
rearranged to solve for either mass or volume:
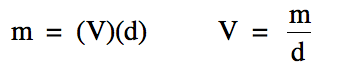
When finding mass or volume, rather
than plugging the measurements given in the problem into one of the two
equations above, we will instead use dimensional analysis with density as a
conversion factor between mass and volume as demonstrated in the following two
problems:
Sample Exercise 1E:
Liquid mercury has a density of
13.6 g/mL.
What is the mass of 7.2 mL of liquid mercury?
Solution:
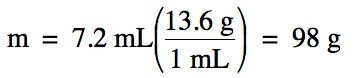
Sample Exercise 1F:
Table salt has a density of 2.2
g/cm3. What is the
volume of 75.5 g of table salt?
Solution:
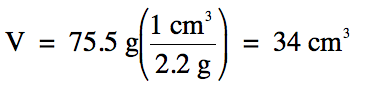
Section 1-5: Experiment – Determining the
Density of a Solid by Water Displacement
The density of a solid can be
determined in a lab using a simple method known as water displacement that
follows the procedure below:
1) Record the mass of the solid.
2) Partially fill a graduated
cylinder with water and record the initial volume of the water.
3) Carefully add the solid to the
graduated cylinder to avoid water splashing out and
then record the final volume of the water and solid combined.
4) Subtract to find the volume of
the solid and then calculate the density of the solid.
Sample Exercise 1G:
In an experiment to determine the
density of a solid by water displacement, a student recorded the following
data:
|
Mass of
Solid |
19.21 g |
|
Initial
Volume of Water |
14.2 mL |
|
Final
Volume of Water + Solid |
15.9 mL |
Based on the experimental data
above, what is the correctly-rounded density of the
solid?
Solution:
[Recall from Section 1-3 that we
always perform all the addition and subtraction steps first using the fewest
decimal places rounding rule followed by the multiplication and division steps
using the fewest sig. fig.s rounding rule.
As a result, it is possible for the final answer to not have the same
number of sig. fig.s as any of the original
measurements given in the problem.]
First, subtract to find the volume
of the solid, but then change the unit from mL to the
equivalent cm3 because mL is not used for
the volume of solids:
15.9
mL – 14.2 mL =
1.7 mL = 1.7 cm3
Note that since both measurements
in the above subtraction step have 1 decimal place, the calculated volume
should have 1 decimal place.
Now simply divide mass by volume to
find density:
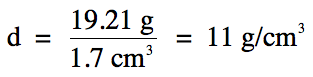
Note that we have now switched over
to the fewest sig. fig.s rounding rule for the above division step. As such, the final answer should have 2
sig. fig.s because the calculated volume of the solid
has 2 sig. fig.s.
Note also that the calculated
density may differ from the true value due to experimental error. For example, if water splashes out of
the graduated cylinder as the solid is added, the final volume recorded will be
too low. As a result, the volume
of the solid found by subtraction will be too low, leading to an erroneously
high density.
Chapter 1 Practice Exercises and Review Quizzes:
(a) 0.00002030
(b) 670.
(c) 1.0800 x 10-5
Click for Solution
1-1) (a)
0.00002030 = 4 sig. fig.s
(b) 670. =
3 sig. fig.s
(c) 1.0800
x 10-5 = 5 sig. fig.s
1-2) Convert the following
measurements:
(a) 0.0070 pounds to milligrams
(b) 0.0900 gallons to milliliters
(c) 9.7 x 106 centimeters to miles
Click for Solution
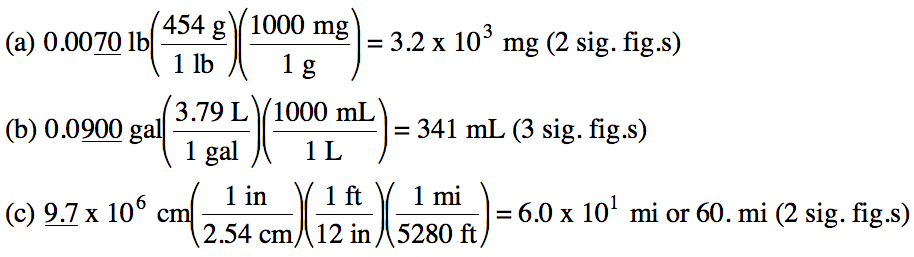
1-3) The density of aluminum metal
is 2.72 g/cm3. What is
the mass in milligrams of 0.36 cm3 of aluminum metal?
Click for Solution
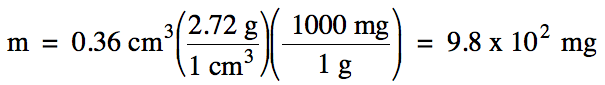
Note that we should round our
calculated answer of 979 up to obtain 2 sig. fig.s using scientific notation
because the volume given in the problem has 2 sig. fig.s.
1-4) The
density of liquid ethanol is 0.79 g/mL. What is the volume in gallons of 0.0475
kilograms of ethanol?
Click for Solution
1-4)
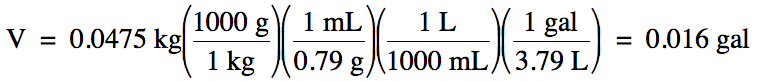
Note that we should round our
calculated answer of 0.0159 up to obtain 2 sig. fig.s because the density
given in the problem has 2 sig. fig.s.
1-5) In an
experiment to determine the density of a solid by water displacement, a student
recorded the following data:
|
Mass of
Solid |
17.2 g |
|
Initial
Volume of Water |
11.3 mL |
|
Final
Volume of Water + Solid |
12.1 mL |
Based on the experimental data
above, what is the correctly-rounded density of the
solid?
Click for Solution
1-5)
12.1
mL – 11.3 mL =
0.8 mL = 0.8 cm3
(subtraction
= round to 1 decimal place)
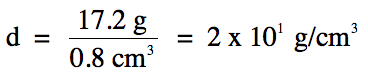
Note that we switch over to the
fewest sig. fig.s rounding rule for the division step, so we should round our
calculated answer of 21.5 down to 1 sig. fig. using
scientific notation because the calculated volume has 1 sig. fig.
