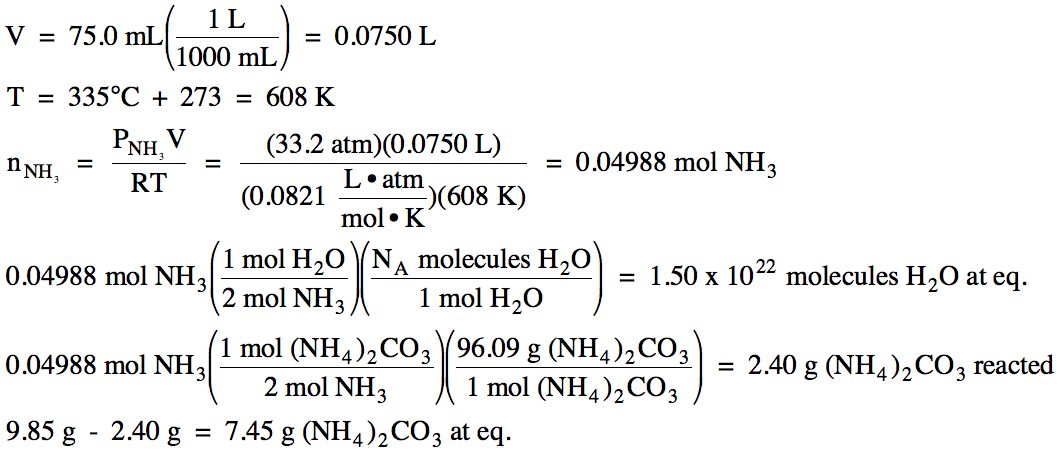Chapter 15: Equilibrium
Section 15-1: Equilibrium Constant, Kc and Kp, Expressions
Section 15-2: Equilibrium Calculations and RICE Charts
Section 15-3: Reaction Quotients, Qc and Qp
Section 15-4: Heterogeneous Equilibria
Section 15-5: Le Châtelier's Principle
Section 15-6: Converting Between Kc and Kp
Section 15-7: Relationship Between ΔG° and Equilibrium Constants
Chapter 15 Practice Exercises and Review Quizzes
Section 15-1: Equilibrium Constant, Kc and Kp,
Expressions
As soon as a chemical reaction is
initiated, the amount of each reactant on the left side of the equation will
begin to decrease, and the rate of the forward reaction (toward the right) will
begin to decrease. At the same
time, the amount of each product on the right side of the equation will begin
to increase, and the rate of the reverse reaction (toward the left) will begin
to increase. Eventually, the rates
of the forward and reverse reactions will become equal and, therefore, the
amounts of the reactants and products will remain constant. A reaction that reaches this point is
said to be at equilibrium, which can be indicated by replacing the forward
arrow (→) in the
chemical equation with a double equilibrium arrow (⇌).
For the discussion that follows,
the notation [X] in an equation indicates that the concentration of X in
moles/liter or M should be inserted into the equation. The notation PX in an
equation indicates that the pressure of X in atm
should be inserted into the equation.
For a reaction aA + bB ⇌ cC + dD, where the lower case letters a through d represent coefficients, the amounts of the products relative to
the reactants present at equilibrium will be indicated by the values Kc and Kp,
known as equilibrium constants, according to the following expressions:
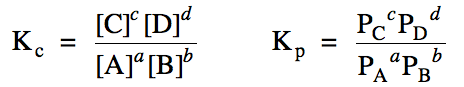
Note that the Kp
expression will not apply if the reaction does not contain gases.
Sample Exercise 15A:
Write the Kc
and Kp (only if applicable) expressions
for each reaction:
(a) N2 (g) + 3 F2
(g) ⇌ 2 NF3
(g)
(b) Sn2+ (aq) + 2 Fe3+ (aq) ⇌ Sn4+
(aq) + 2 Fe2+ (aq)
Solution:
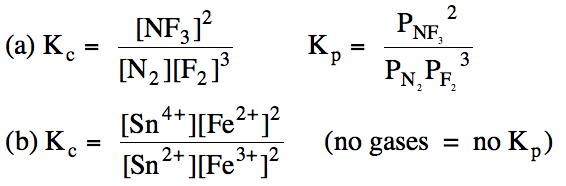
Once we have written a Kc expression, we can substitute the equilibrium
molarities for each reactant and product to calculate the numerical value of Kc. Similarly, once we have written a Kp expression, we can substitute the equilibrium
pressures in atm for each reactant and product to
calculate the numerical value of Kp:
Sample Exercise 15B:
For reaction (a) above, calculate
the value of Kp given the following
equilibrium pressures:
nitrogen gas = 0.125 atm
fluorine gas = 0.85 atm
nitrogen trifluoride gas = 0.40 atm
Solution:
Equilibrium constant values are
typically expressed without units, so we substitute the pressure in atm of each reactant and product, but without including
units, into the Kp expression:
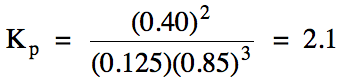
If we know the value of Kp and all but one pressure in the expression,
we can calculate the unknown pressure.
Similarly, if we know the value of Kc and
all but one molarity in the expression, we can
calculate the unknown molarity:
Sample Exercise 15C:
For reaction (b) above, Kc = 37.
Calculate the equilibrium molarity of iron(III) ions given the following equilibrium molarities:
tin(II) = 0.12 M
tin(IV) = 0.28 M
iron(II) = 0.36 M
Solution:
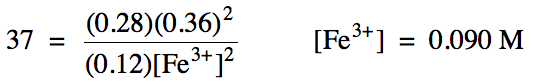
Note that we must always include a
unit when solving for an equilibrium molarity or
pressure.
If a reaction is written in the
reverse direction, the equilibrium constant for the new reaction will be the
reciprocal of the original equilibrium constant:
A ⇌ B equilibrium constant
= K
B ⇌ A equilibrium constant
= 1/K
If the coefficients of a reaction
are multiplied by an integer or fraction x, the equilibrium constant for the
new reaction will have a value equal to the original equilibrium constant
raised to the x power:
A ⇌ B equilibrium constant
= K
xA ⇌ xB equilibrium constant
= (K)x
Sample Exercise 15D:
For the reaction N2 (g)
+ 3 F2 (g) ⇌ 2 NF3
(g), the value of Kp = 2.1. Calculate the value of Kp for the following reaction:
NF3
(g) ⇌ 1/2 N2
(g) + 3/2 F2 (g)
Solution:
To obtain the new reaction, the
original reaction was reversed and also the coefficients were multiplied by
1/2. Therefore, we can either take the reciprocal of the original Kp
value and then raise the result to the 1/2 power, or we can raise the
original Kp value to the 1/2 power and
then take the reciprocal of the result.
The same answer will be achieved using either method:
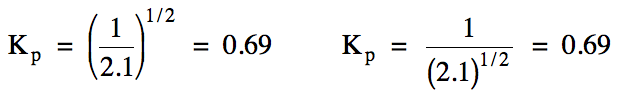
If two or
more reactions are added, the equilibrium constant for the new reaction will
the be product of the equilibrium constants for each reaction that was added:
A ⇌ B equilibrium constant
= K1
C ⇌ D equilibrium constant
= K2
A + C ⇌ B + D equilibrium constant
= (K1)(K2)
Section 15-2: Equilibrium Calculations and RICE Charts
In the numerical examples above,
the given molarities could be substituted into the Kc
expression and the given pressures could be substituted into the Kp expression because they represented the
amounts of reactants and products at equilibrium. If instead we are given initial
molarities or pressures before the reaction has begun, we must use stoichiometry to determine how the molarity
or pressure of each reactant and product changes as the reaction proceeds until
equilibrium is reached. Only after
we have determined the final molarity or pressure of
each reactant and product at equilibrium can we substitute those values
into the Kc or Kp
expression.
A
Reaction-Initial-Change-Equilibrium or RICE chart is a convenient way to
organize equilibrium stoichiometry calculations. The four lines of a RICE chart are as
follows:
R = Write the reaction.
I = Write the initial molarities (for calculations
involving Kc) or pressures in atm (for calculations involving Kp)
for each reactant and product, but units may be omitted on the RICE chart.
C = Write the change in the molarity
or pressure of each reactant and product as the reaction proceeds. We will begin completing this line by
representing the change in the molarity or pressure
of one reactant or product as +x if the change is known to be an increase or
–x if the change is known to be decrease. We will then use the coefficients of the reaction and stoichiometric ratios to deduce the change in all other
reactants and products in terms of x.
E = Write the molarity or pressure
of each reactant and product at equilibrium in terms of x. Each value on this line will simply be
the sum of the values on the Initial and Change lines (I + C = E).
After completing a RICE chart, if
the molarity or pressure of one reactant or product at
equilibrium has been given, we can determine the numerical value of x. Once x is known, we can deduce the
molarities or pressures of all other reactants and products at equilibrium,
after which we can substitute these values into the Kc
or Kp expression to find the numerical
values of Kc or Kp:
Sample Exercise 15E:
(a) Write the Kc
expression for the reaction 2 H2S (g) + CH4 (g) ⇌ CS2
(g) + 4 H2 (g).
(b) H2S gas with an
initial concentration of 0.37 M and methane gas with an initial concentration
of 0.42 M are placed in an empty container and a reaction is initiated. When equilibrium is reached, the
concentration of hydrogen gas is found to be 0.52 M. Calculate the concentrations of each gas at equilibrium and
also the value of Kc for the reaction.
Solution:
(a)
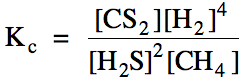
(b) We begin by creating a RICE
chart showing the initial molarities of each reactant and product. Note that the initial molarities of only
H2S and CH4 were specified, so we can assume that CS2
and H2 each have an initial molarity equal
to zero. Since the initial
molarities of CS2 and H2 are zero and, therefore, must
increase as the reaction proceeds, we make the signs of the changes positive
for CS2 and H2.
If the signs of the changes on the right side are positive, then the
signs of the changes on the left side must be negative to represent a decrease
in the molarities of H2S and CH4 as the reaction
proceeds:
|
R |
2 H2S (g) + CH4
(g) ⇌ CS2
(g)
+ 4 H2 (g) |
|||
|
I |
0.37 |
0.42 |
0 |
0 |
|
C |
- |
- |
+ |
+ |
|
E |
|
|
|
|
If we define the change in molarity of CS2 as +x, then according to the 4:1
stoichiometric ratio from the coefficients of the
reaction, the change in molarity of H2
will be +4x. Using the same
method, the change in molarity of H2S will
be -2x and the change in molarity of CH4
will be –x. After completing
the C line, we add the I and C lines to obtain the values in the E line in
terms of x:
|
R |
2 H2S (g) + CH4
(g) ⇌ CS2
(g)
+ 4 H2 (g) |
|||
|
I |
0.37 |
0.42 |
0 |
0 |
|
C |
-2x |
-x |
+x |
+4x |
|
E |
0.37-2x |
0.42-x |
x |
4x |
From the information given in the
problem, we know that the equilibrium molarity of H2
is 0.52 M, which allows us to determine the numerical value of x and
equilibrium molarities of the other gases as follows:
[H2]
= 0.52 M = 4x
x = 0.13 M = [CS2]
[H2S]
= 0.37-2x = 0.37-2(0.13) = 0.11 M
[CH4]
= 0.42-x = 0.42-0.13 = 0.29 M
Finally, we substitute the
equilibrium molarities of each gas into the Kc
expression to obtain the value of Kc:
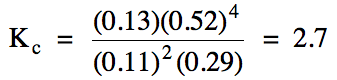
If we are given the value of Kc or Kp in
a RICE chart problem rather than any of the equilibrium molarities or
pressures, we can solve the Kc or Kp expression for x:
Sample Exercise 15F:
(a) Write the Kp
expression for the reaction CO (g) + 2 H2 (g) ⇌ CH3OH
(g).
(b) Carbon monoxide gas with an
initial pressure of 38 atm and hydrogen gas with an initial pressure of 56 atm
are placed in an empty container and a reaction is initiated. If Kp
= 9.5 x 10-3 for this reaction, calculate the equilibrium pressure
of each gas.
(c) Calculate the total pressure at
equilibrium.
Solution:
(a)
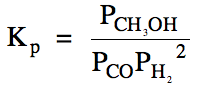
(b) First, we complete the RICE
chart in terms of x:
|
R |
CO (g) + 2 H2 (g) ⇌ CH3OH
(g) |
||
|
I |
38 |
56 |
0 |
|
C |
-x |
-2x |
+x |
|
E |
38-x |
56-2x |
x |
We then substitute the equilibrium
pressures in terms of x into the Kp
expression and solve for x, after which we can determine the equilibrium
pressures of each gas:
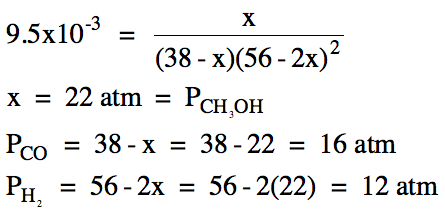
The equation above can be solved
for x using a graphing calculator, keeping in mind that the value of x must be
always be a real number greater than zero and also that the value of x cannot
be so large as to result in a negative equilibrium molarity
or pressure for any reactant or product.
For the equation being solved above, since x > 0 and 56-2x > 0, we
know that the correct root must have 0 < x < 28.
(c) To find the total pressure at
equilibrium, we simply add together the equilibrium pressures of all the gases:
Ptotal = 16 atm
+ 12 atm + 22 atm = 50. atm
If one or more of the reactants on
the left side of an equation have an initial molarity
or pressure equal to zero, then the reaction will proceed in the reverse
direction and, thus, the RICE chart changes will be positive for each of the
reactants on the left while being negative for each of the products on the
right:
Sample Exercise 15G:
(a) Write the Kc
expression for the reaction Sn4+ (aq) + 2
Cr2+ (aq) ⇌ Sn2+ (aq) + 2 Cr3+ (aq).
(b) A reaction mixture is prepared
with the following initial concentrations:
chromium(II) = 0.46 M
tin(II) = 0.65 M
chromium(III) = 0.72 M
If Kc
= 0.40 for this reaction, calculate the equilibrium molarity
of each ion.
Solution:
(a)
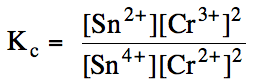
(b)
|
R |
Sn4+ (aq)
+
2 Cr2+ (aq) ⇌ Sn2+ (aq) + 2 Cr3+ (aq) |
|||
|
I |
0 |
0.46 |
0.65 |
0.72 |
|
C |
+x |
+2x |
-x |
-2x |
|
E |
x |
0.46+2x |
0.65-x |
0.72-2x |
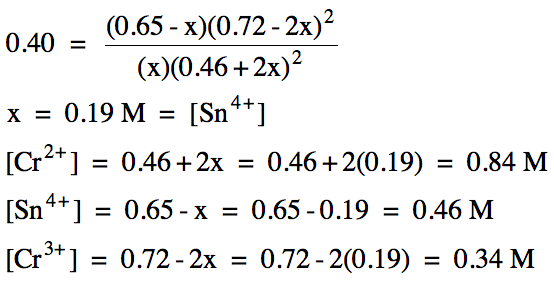
(x > 0 and 0.72-2x > 0, so 0 < x < 0.36)
Section 15-3: Reaction Quotients, Qc and Qp
For a reaction aA + bB⇌ cC + dD, if none of the reactants or
products have an initial molarity or pressure equal
to zero and if we are not given the molarity or pressure of any reactant or product at equilibrium, we cannot determine by simple inspection whether the reaction proceeds in the forward or reverse direction to reach equilibrium. In these cases, we must first calculate
a reaction quotient Qc or Qp by
entering the initial (i) molarities or pressures of each reactant and product into
one of the following expressions:
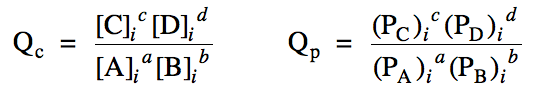
After Qc or Qp has been calculated, we can determine the
direction that the reaction must proceed to reach equilibrium as follows:
If Qc < Kc or Qp
< Kp, the reaction must proceed in the
forward direction to reach equilibrium.
Therefore, the RICE chart changes for the products on the right will be
positive while the changes for the reactants on the left will be negative.
If Qc > Kc or Qp
> Kp, the reaction must proceed in the
reverse direction to reach equilibrium.
Therefore, the RICE chart changes for the reactants on the left side
will be positive while the changes for the products on the right side will be
negative.
Note that if Qc = Kc or Qp = Kp, then the reaction is already at equilibrium
and, therefore, the initial molarities or pressures given are equal to the
equilibrium molarities or pressures.
Sample Exercise 15H:
(a) For the reaction 2 SO2
(g) + O2 (g) ⇌ 2 SO3
(g), Kp = 0.85. In which direction must this reaction proceed to reach
equilibrium starting with the following initial pressures?:
sulfur dioxide gas = 0.66 atm
oxygen gas = 0.51 atm
sulfur trioxide gas = 0.98 atm
(b) Calculate the equilibrium
pressure of each gas.
(c) Calculate the total pressure at
equilibrium.
Solution:
(a) We first calculate Qp and then compare to Kp:
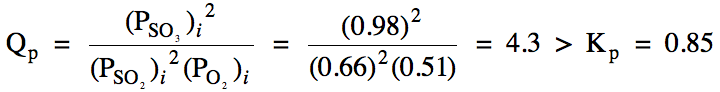
Since Qp
> Kp, the reaction will proceed in the
reverse direction to reach equilibrium.
(b)
|
R |
2SO2 (g) + O2
(g) ⇌ 2 SO3
(g) |
||
|
I |
0.66 |
0.51 |
0.98 |
|
C |
+2x |
+x |
-2x |
|
E |
0.66+2x |
0.51+x |
0.98-2x |
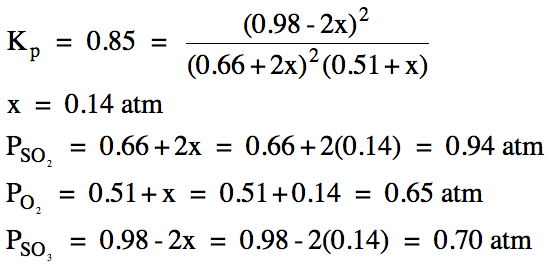
(x > 0 and 0.98-2x > 0, so 0 < x < 0.49)
(c) Ptotal
= 0.94 atm + 0.65 atm +
0.70 atm = 2.29 atm
Section 15-4: Heterogeneous Equilibria
Reactions that involve only a
single state of matter are said to be homogeneous. All of the reactions above that involve only gaseous or only
aqueous reactants and products are homogeneous. Reactions that involve more than one state of matter are
said to be heterogeneous. When Kc, Kp, Qc,
and Qp expressions for heterogeneous
reactions are written, solids and liquids are omitted from the expressions:
Sample Exercise 15I:
(a) Write the Kc
and Kp expressions for the reaction 4 KO2
(s) + 2 CO2 (g) ⇌ 2 K2CO3
(s) + 3 O2 (g).
(b) Calculate Kp
for this reaction if the equilibrium pressure of carbon dioxide gas is 13 atm and the equilibrium pressure of oxygen gas is 17 atm.
Solution:
(a)
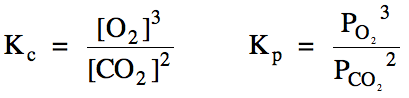
(b)
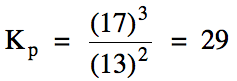
On a RICE chart for a heterogeneous
reaction, the columns under solids and liquids will be left blank. However, we can still calculate changes
in the amounts of solids and liquids as the reaction proceeds using standard stoichiometry with mole ratios:
Sample Exercise 15J:
(a) Write the Kp expression for the decomposition of solid ammonium carbonate to form ammonia gas, carbon dioxide gas, and liquid water:
(NH4)2CO3
(s) ⇌ 2 NH3
(g) + CO2 (g) + H2O (l)
(b) After a 9.85 gram sample of solid ammonium carbonate was placed in a 75.0 mL container and heated to 335°C, the total pressure at equilibrium was found to be 49.8 atm. Calculate the equilibrium pressure of each gas and Kp for this reaction.
(c) Calculate the number of water
molecules and the mass of solid ammonium carbonate present at equilibrium.
Solution:
(a)
![]()
(b)
|
R |
(NH4)2CO3
(s) ⇌ 2 NH3
(g) +
CO2 (g) + H2O
(l) |
|||
|
I |
|
0 |
0 |
|
|
C |
+2x |
+x |
||
|
E |
2x |
x |
||
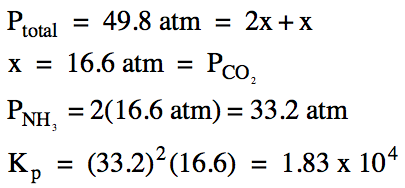
(c) We first use the Ideal Gas Law
to convert the equilibrium pressure of ammonia to find the moles of ammonia
formed in the reaction. Then we
can use a mole ratio from the balanced equation to find the moles of water
formed in the reaction, after which we use Avogadro's number to convert to
water molecules present at equilibrium.
Next, we again use a mole ratio to find the moles of ammonium carbonate
that reacted to make the products, after which we use the molar mass to convert
to grams. Finally, we subtract the
mass of ammonium carbonate reacted from the initial mass to find the final mass
of ammonium carbonate present at equilibrium:
Note that we could have arrived at
the same answers by first finding the moles of carbon dioxide gas formed in the
reaction rather than first finding the moles of ammonia gas formed in the
reaction.
Section 15-5: Le Châtelier's Principle
A variety of factors may cause a
reaction at equilibrium to temporarily fall out of equilibrium. Le Châtelier's
Principle essentially states that a reaction which has fallen
out of equilibrium will respond by proceeding at unequal forward and
reverse rates until equilibrium has been reestablished. A reaction that proceeds faster in the
forward direction is said to shift to the right. When a reaction shifts to the right, the amount of products
on the right side of the equation will increase and the amount of reactants on
the left side of the equation will decrease. A reaction that proceeds faster in the reverse direction is
said to shift to the left. When a
reaction shifts to the left, the amounts of reactants on the left side of the
equation will increase and the amount of products on the right side of the
equation will decrease. According
to Le Châtelier's Principle, the following guidelines
predict what will occur when a variety of changes are made to a reaction at
equilibrium:
1a. (g) or
(aq) reactant is added = shifts right
1b. (g) or
(aq) product is added = shifts left
2a. (g) or
(aq) reactant is removed = shifts left
2b. (g) or
(aq) product is removed = shifts right
3a. (s) or
(l) reactant or product is added = no shift
3b. (s) or (l) reactant or product is removed = no shift
4a. Volume of reaction container is
increased = shifts in direction having more moles of (g) [sum of coefficients
for (g) only is greater]
4b. Volume of reaction container is
decreased = shifts in direction having fewer moles of (g) [sum of coefficients
for (g) only is less]
5a. Water is added to increase
volume of solution = shifts in direction having more moles of (aq) [sum of coefficients for (aq)
only is greater]
5b. Water is evaporated to decrease
volume of solution = shifts in direction having fewer moles of (aq) [sum of coefficients for (aq)
only is less]
6. Catalyst is added = both forward
and reverse rates increase but remain equal = no shift
7a. Inert (unreactive)
gas (for example: noble gases
helium, neon, argon) added with no change in volume of reaction container = no
shift
7b. Inert gas added with no change in pressure = volume must increase = shifts in direction having more moles of (g)
8a. Temperature is increased =
shifts in endothermic direction (ΔH > 0)
8b. Temperature is decreased =
shifts in exothermic direction (ΔH < 0)
Note that the ΔH value listed after
a reaction refers to the forward direction. Therefore, for the reaction A ⇌ B ΔH < 0, the reaction is exothermic in the forward
direction and endothermic in the reverse direction.
Of the changes listed above, only a change in temperature will change
the value of Kc and Kp. If the reaction shifts right due to a
temperature change, then Kc and Kp will increase. If the reaction shifts left due to a temperature change, Kc and Kp
will decrease.
Sample Exercise 15K:
Consider the reaction:
2 H2O
(g) + 3 S (s) ⇌ 2 H2S
(g) + SO2 (g) ΔH > 0
(a) State whether the amount of H2S
gas present at equilibrium will increase, decrease, or remain unchanged when
each of the following occurs:
i. Sulfur
dioxide gas is added.
ii. Water vapor is removed.
iii. Solid sulfur is removed.
iv. The container volume is
increased.
v. A catalyst is added.
vi. Argon gas is added at constant volume.
vii. Helium gas is added at constant pressure.
viii. The temperature is decreased.
(b) Of the changes above, which
will change the value of Kc and Kp, and will Kc
and Kp increase or decrease?
Solution:
(a)
i. Add (g)
product = shifts left = amount of
H2S decreases (guideline 1b).
ii. Remove (g) reactant = shifts
left = amount of H2S decreases (guideline 2a).
iii. Remove (s)
reactant = no shift = amount of H2S unchanged (guideline 3b).
iv. Volume of container increases =
shifts to side with more (g) moles.
Although total moles is larger on left (5 ⇌ 3), there are more (g)
moles on the right (2 ⇌ 3), so
shifts right = amount of H2S increases (guideline 4a).
v. Catalyst is added = no shift =
amount of H2S unchanged (guideline 6).
vi. Inert gas added with no volume change = no shift = amount of H2S unchanged (guideline 7a).
vii. Inert gas added with no pressure
change = volume increases = shifts to side with more (g) moles = shifts right = amount of H2S increases (guideline 7b).
viii. Temperature decreases =
shifts in exothermic direction = shifts left = amount of H2S
decreases (guideline 8b).
(b) Only a temperature change will
change the value of Kc and Kp.
Reaction shifts left when temperature is decreased, so Kc and Kp
decrease.
Section 15-6: Converting Between Kc and Kp
We can use the following equation
to convert between Kc and Kp:
Kp = Kc(RT)Δn of gas
When using the equation above, we
will not show units in the calculation, but we must use R = 0.0821 and the
temperature T in K. The exponent
“Δn of gas” is found by subtracting the sum of only (g) coefficients for
reactants on the left side of the equilibrium reaction from the sum of only (g)
coefficients for products on the right side of the equilibrium reaction:
Sample Exercise 15L:
If Kp = 7.5 x 104 at 65°C for the reaction S (s) + 2 HI (g) ⇌ I2 (s) + H2S (g), calculate Kc for the reaction at 65°C.
Solution:
Do not include solids:
7.5 x 104 = Kc(0.0821 x 338)1 - 2 = -1
Kc = 2.1 x 106
We will demonstrate converting from
Kc to Kp in Sample Exercise 15M.
Section 15-7: Relationship Between ΔG° and
Equilibrium Constants
A chemical reaction with a more
negative ΔG° will have larger values of Kc and Kp and,
therefore, larger amount of products relative to reactants at equilibrium. A chemical reaction with a more
positive ΔG° will have smaller values of Kc and Kp and,
therefore, smaller amount of products relative to reactants at
equilibrium. Although Kc and Kp for a given reaction are known as equilibrium constants, note
that their values will change when the temperature is changed.
We can use the following equation
to convert between ΔG° and an equilibrium constant:
ΔG° = -RTlnKeq
When using the equation above, we
must use R = 8.31 J/mol•K and the temperature T in K. For reactions with at least one (aq) reactant or product but
no (g), Kc should be substituted for Keq in the
equation. For reactions with at
least one (g) reactant or product but no (aq), Kp should be
substituted for Keq in the equation. We will not focus on reactions that involve both (aq) and
(g).
Sample Exercise 15M:
If Kc = 0.00155 at 175°C
for the reaction NO2 (g) ⇌ NO (g) + 1/2 O2 (g), calculate ΔG° for the reaction at 175°C.
Solution:
Since the reaction involves (g) but
no (aq), first convert Kc to Kp and then substitute Kp for Keq to calculate ΔG°:
Kp = 0.00155(0.0821 x 448)(1 + 1/2) - 1 = 1/2 = 0.00940
ΔG° = -8.31
J/mol•K(448 K)ln(0.00940) = 1.74 x 104 J/mol = 17.4 kJ/mol
Sample Exercise 15N:
If ΔG° = 15.6 kJ/mol at 25°C for
the reaction LiF (s) ⇌ Li+ (aq) + F- (aq), calculate Kc for the reaction at
25°C.
Solution:
Since the reaction involves (aq)
but no (g), substitute Kc for Keq. Also, use ΔG° in J/mol:
1.56 x 104 J/mol = -8.31 J/mol•K(298 K)lnKc
Kc = 0.00184
Chapter 15 Practice Exercises and Review Quizzes:
15-1) (a)
Write the Kc and Kp
expressions for the reaction Hg (l) + 1/2 O2 (g) ⇌ HgO (s).
(b) If
Kp = 9.5 for this reaction, calculate the
equilibrium pressure of oxygen gas.
Click for Solution
15-1) (a)
Heterogeneous reaction = omit solids and liquids from Kc
and Kp expressions:
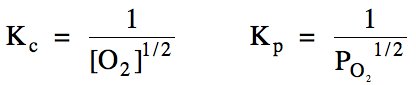
(b)
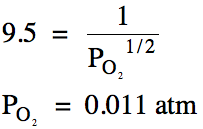
15-2) For
the reaction Hg (l) + 1/2 O2 (g) ⇌ HgO
(s), the value of Kc = 47. Calculate the value of Kc for the following reaction:
2 HgO (s) ⇌ 2 Hg (l) +
O2 (g)
Click for Solution
15-2) Reverse original reaction and
multiply coefficients by 2 = either take reciprocal of original Kc and then raise result to the 2 power or raise
original Kc to the 2 power and then take
reciprocal of result:

15-3) (a)
Write the Kp expression for the reaction 4
HCl (g) + O2 (g) ⇌ 2 Cl2
(g) + 2 H2O (g).
(b) HCl gas with an initial pressure of 0.17 atm and oxygen gas with an initial pressure of 0.58 atm are placed in a container along with chlorine gas with
an initial pressure of 0.92 atm and water vapor with
an initial pressure of 0.83 atm.
When equilibrium is reached, the pressure of HCl
gas is found to be 0.81 atm. Calculate
the equilibrium pressures of each gas, the total pressure at equilibrium, and Kp for the reaction.
Click for Solution
15-3) (a)
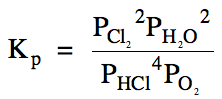
(b) Since the pressure
of HCl has increased from 0.17 atm
to 0.81 atm, then the
reaction must have proceeded in the reverse direction to reach
equilibrium. Therefore, the changes
for the reactants on the left side of the RICE chart will be positive while the
changes for the products on the right side will be negative:
|
R |
4 HCl
(g) + O2
(g)
⇌ 2 Cl2
(g)
+
2 H2O (g) |
|||
|
I |
0.17 |
0.58 |
0.92 |
0.83 |
|
C |
+4x |
+x |
-2x |
-2x |
|
E |
0.17+4x |
0.58+x |
0.92-2x |
0.83-2x |
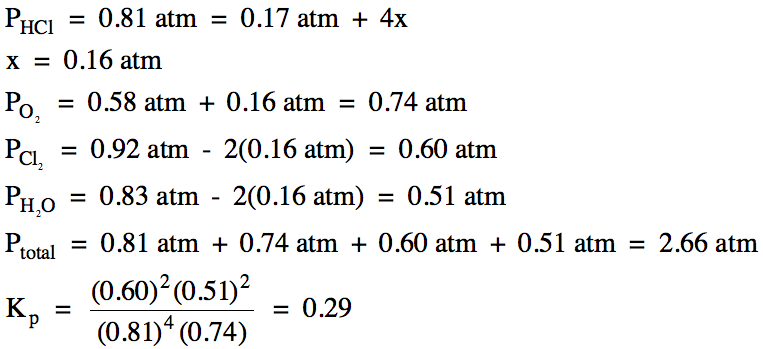
15-4) For
the reaction 2 Al (s) + 3 Sn4+ (aq) ⇌ 2 Al3+
(aq) + 3 Sn2+ (aq),
Kc = 0.0011. Solid aluminum metal is added to a solution containing the
initial concentrations 0.18 M Sn4+, 0.59 M Al3+, and 0.97
M Sn2+. Calculate the molarity of each ion at equilibrium.
Click for Solution
15-4) Heterogeneous reaction = omit
solid from Qc expression, RICE chart, and Kc
expression:
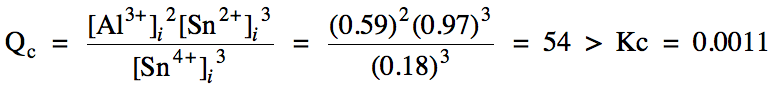
Since Qc > Kc, the reaction will proceed in the reverse
direction to reach equilibrium:
|
R |
2 Al (s) +
3 Sn4+ (aq) ⇌ 2 Al3+ (aq) + 3 Sn2+ (aq) |
|||
|
I |
|
0.18 |
0.59 |
0.97 |
|
C |
+3x |
-2x |
-3x |
|
|
E |
0.18+3x |
0.59-2x |
0.97-3x |
|
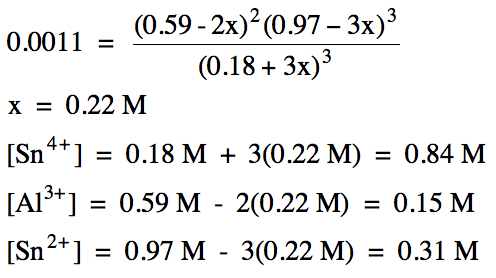
15-5) (a) Write the Kc expression for the decomposition of solid sodium bicarbonate to form solid sodium oxide, carbon dioxide gas, and water vapor:
2
NaHCO3 (s) ⇌ Na2O
(s) + 2 CO2 (g) + H2O (g)
(b) An
8.2 gram sample of solid sodium bicarbonate was partially
decomposed in a 225 mL container. If Kc
= 0.0040 for the decomposition reaction, calculate the equilibrium molarity of each gas and the mass of each solid present at
equilibrium.
Click for Solution
15-5) (a) Kc = [CO2]2[H2O]
(b)
|
R |
2 NaHCO3 (s) ⇌ Na2O (s) +
2CO2 (g) + H2O
(g) |
|||
|
I |
|
|
0 |
0 |
|
C |
+2x |
+x |
||
|
E |
2x |
x |
||
0.0040 = (2x)2(x)
x = 0.10 M = [H2O]
[CO2]
= 2(0.10 M) = 0.20 M
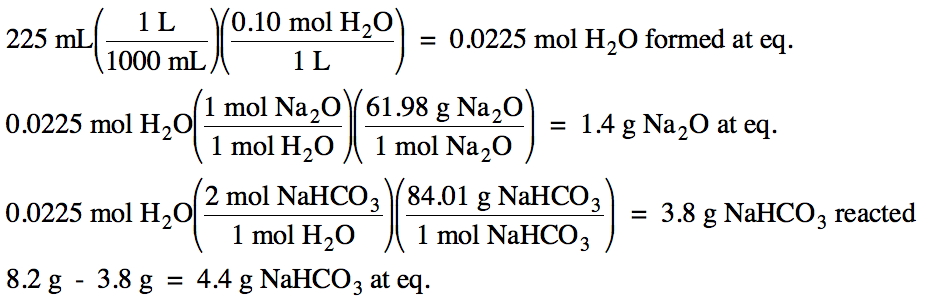
15-6) Consider
the reaction:
4 H2
(g) + Fe3O4 (s) ⇌ 4 H2O (g) + 3 Fe
(s) ΔH
> 0
(a) State whether the amount of
water vapor present at equilibrium will increase, decrease, or remain unchanged
when each of the following occurs:
i. Solid
iron metal is added.
ii. A catalyst is added.
iii. The volume of the container is
decreased.
iv. Neon gas is added at constant
volume.
v. The temperature is increased.
vi. Hydrogen gas is removed.
vii. Argon gas is added at constant pressure
(b) Of the changes above, which
will change the value of Kc and Kp, and will Kc
and Kp increase or decrease?
Click for Solution
15-6)
(a)
i. Add (s)
product = no shift = amount of water vapor unchanged (guideline 3a).
ii. Add catalyst = no shift =
amount of water vapor unchanged (guideline 6).
iii. Volume of container decreases
= shifts to side with fewer (g) moles.
Although total moles is less on left (5 ⇌ 7), there are equal (g)
moles on both sides (4 ⇌ 4), so no
shift = amount of water vapor unchanged (guideline 4b).
iv. Inert gas added with no volume
change = no shift = amount of water vapor unchanged (guideline 7a).
v. Temperature increases = shifts
in endothermic direction = shifts right = amount of water vapor increases
(guideline 8a).
vi. Remove (g) reactant = shifts
left = amount of water vapor decreases (guideline 2a).
vii. Inert gas added with no pressure
change = volume increases = shifts to side with more (g) moles = no shift because equal (g) moles on both sides = amount of water vapor unchanged (guideline 7b).
(b) Only a temperature change will
change the value of Kc and Kp.
Reaction shifts right when temperature increases, so Kc
and Kp increase.
15-7) If Kp = 0.18 at 975°C for the reaction CO (g) ⇌ 1/2 CO2 (g) + 1/2 C (s), calculate Kc for the reaction at 975°C.
Click for Solution
15-7) Do not include solid:
0.18 = Kc(0.0821
x 1248)1/2 - 1 = -1/2
Kc = 1.8
15-8) If Kc = 0.00645 at 675°C for the reaction 3H2 (g) + CO (g) ⇌ H2O (g) + CH4 (g), calculate ΔG° for the reaction at 675°C.
Click for Solution
Kp = 0.00645(0.0821 x 948)(1+1) - (3+1) = -2 = 1.06 x 10-6
ΔG° = -8.31 J/mol•K(948 K)ln(1.06 x 10-6) = 1.08 x 105 J/mol = 108 kJ/mol
15-9) If ΔG° = 10.6 kJ/mol at 25°C for the reaction HClO2 (aq) ⇌ H+ (aq) + ClO2- (aq), calculate Kc for the reaction at 25°C.
Click for Solution
1.06 x 104 J/mol = -8.31 J/mol•K(298 K)lnKc
Kc = 0.0138
Click for Review Quiz 1 Answers