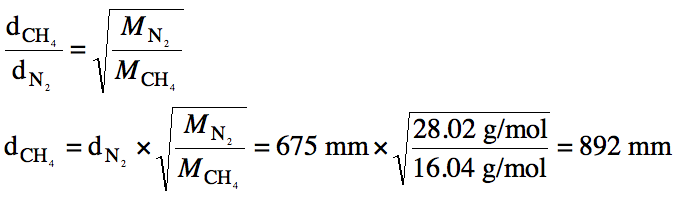Chapter 5: Gases

Section 5-3: Determining Molar Mass of a Gas and Gas Density

Section 5-4: Other Gas Laws

Section 5-5: Measuring Pressure with Barometers and Manometers

Section 5-6: Collecting Gases Over Water

Section 5-7: Experiment - Determining the Gas Constant R

Section 5-8: Graham's Law

Chapter 5 Practice Exercises and Review Quizzes

Section 5-1: The Ideal Gas Law

The following variables will be used to represent different gas properties:

Variable	Gas Property
n	moles
P	pressure
T	temperature
V	volume

The four gas properties above are related through an equation known as the Ideal Gas Law:

PV = nRT

When using the Ideal Gas Law with the gas constant R = 0.0821 L•atm/mol•K, we must ensure the following:

1. The pressure must be in the unit atmospheres (atm). Since some lab equipment will give the pressure in the unit millimeters of mercury (mmHg) or the equivalent torr, you may need the following conversion:

1 atm = 760 mmHg = 760 torr

2. The temperature must be in the unit kelvin (K). Since some lab thermometers will give the temperature in degrees Celsius (°C), you may need the following conversion:

T(K) = T(°C) + 273

Note that the temperature conversion above involves addition, so the number of sig. fig.s may change. For example, a temperature of 22°C with 2 sig. fig.s will be the equivalent of 22 + 273 = 295 K and, thus, the temperature is considered to have 3 sig. fig.s during calculations that may follow.

3. The volume must be in the unit liters.

If we know any 3 of the 4 variables above, we can solve the Ideal Gas Law for the unknown variable, as demonstrated in the following problems:

Sample Exercise 5A:

(a) A gas at Standard Temperature and Pressure (STP) has a temperature of 273 K and a pressure of 1.00 atm. What is the volume of 1.00 mole of gas at STP?

(b) A 0.120 g sample of CH₄ gas occupies a volume of 200. mL at 35°C. What is the pressure of the gas in mmHg?

Solution:

(a)

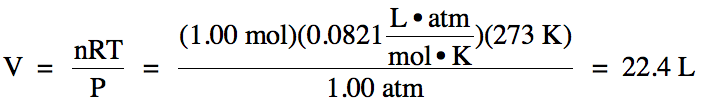
(b)

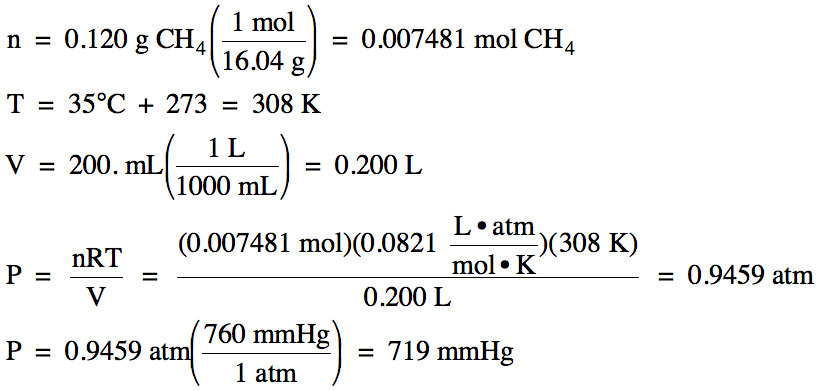
Section 5-2: Gas Stoichiometry

For reactions involving at least one gas, we can use the Ideal Gas Law to convert to and/or from moles in stoichiometry problems, as demonstrated below:

Sample Exercise 5B:

Given the unbalanced equation below, what mass of solid sodium must react to produce 845 mL of hydrogen gas, measured at 21°C and 707 torr?

Na(s) + H₂O (l) → NaOH (aq) + H₂ (g)

Solution:

For reactions involving at least one gas, the Ideal Gas Law can also be used to convert to and/or from moles in limiting reagent and percent yield problems.

Section 5-3: Determining Molar Mass of a Gas and Gas Density

If we measure the pressure, temperature, and volume of an unknown gas, we can solve the Ideal Gas Law for moles. If we also know the mass of the gas, we can divide the mass by the moles to determine the molar mass of the unknown gas:

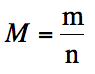
If we have determined the empirical formula of the unknown gas, we can use the molar mass we have calculated to determine the molecular formula of the unknown gas, as demonstrated in the problem below:

Sample Exercise 5C:

An unknown gas has the empirical formula CH₂. A 0.82 gram sample of the gas was found to occupy 5.0 x 10² mL at 23°C and 724 mmHg. Determine the molar mass and molecular formula of the unknown gas.

Solution:

We can use the Ideal Gas Law to substitute for moles in the molar mass equation above:

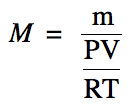
We can then solve this equation for mass divided by volume to derive a new equation for gas density:

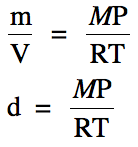
Note that we must use the same units for P and T in the gas density equation that we used in the Ideal Gas Law and also that the unit of the calculated density will be g/L, as demonstrated in the following problem:

Sample Exercise 5D:

What is the density of H₂S gas at 45°C and 787 torr?

Solution:

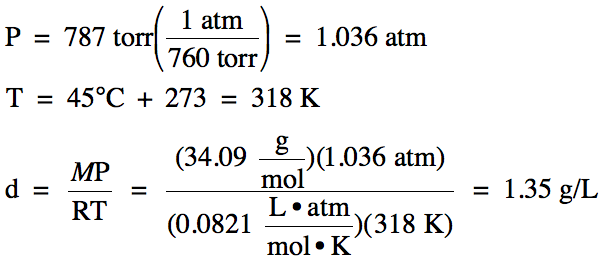
Section 5-4: Other Gas Laws

When two or more properties of a gas change from a known initial (i) set of values and all but one of the final (f) values are known, the General Gas Law can be used to calculate the unknown final value:

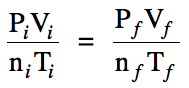
When using the General Gas Law, note the following:

1. The pressure must be in the same unit on both sides of the equation but does not necessarily need to be changed to atm and can remain in mmHg or torr.

2. The volume must be in the same unit on both sides of the equation but does not necessarily need to be changed to L and can remain in mL.

3. The temperature must be in K on both sides of the equation!!!

4. Any of the above properties that are not mentioned can be assumed to be unchanged and, thus, can be eliminated from both sides of the equation, as demonstrated in the following problem:

Sample Exercise 5E:

A sample of gas occupies a volume of 245 mL at 25°C and 685 mmHg. What will be the new volume of the gas if the temperature is increased to 75°C and the pressure in increased to 890. mmHg?

Solution:

Since moles are not mentioned, we can assume n is unchanged and can be eliminated from the General Gas Law, after which we can solve for final volume:

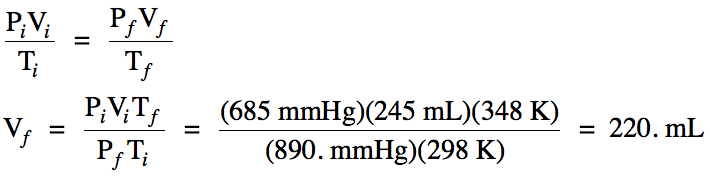
In cases where moles and temperature are unchanged, Boyle's Law essentially states that the pressure and volume of a gas are inversely proportional, which can be represented mathematically by the following equation:

In cases where moles and pressure are unchanged, Charles's Law essentially states that the volume and temperature in K of a gas are directly proportional, which can be represented mathematically by the following equation:

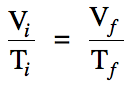
In a mixture of three different gases A, B, and C, the partial pressure of gas A can be represented as P_A, the partial pressure of gas B can be represented as P_B, and the partial pressure of gas C can be represented as P_C. Dalton’s Law of partial pressures essentially states that the total pressure of a gas mixture is simply the sum of the partial pressures of each gaseous component:

P_total = P_A + P_B + P_C

The ratio of the partial pressure of A to the total pressure of the mixture is equal to the mole fraction of A, which is the ratio of the moles of A to the total moles of gas in the mixture:

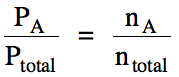
Therefore, the partial pressure of A can be calculated by multiplying the mole fraction of A by the total pressure of the mixture:

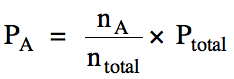
Sample Exercise 5F:

A gaseous mixture of 0.24 mol helium, 0.12 mol neon, and 0.36 mol argon has a total pressure of 0.96 atm. Calculate the partial pressure of each gas in the mixture.

Solution:

Section 5-5: Measuring Pressure with Barometers and Manometers

The pressure exerted by the collection of gases in the atmosphere on the surface below can be measured using a barometer and is known as the barometric pressure, P_bar. A typical barometer consists of an evacuated tube with one closed end and one open end that is inserted into a container of liquid mercury, as shown below:

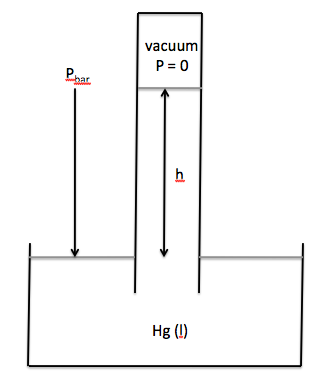
The barometric pressure will be equal to the height to which the mercury is forced up the tube:

P_bar = h in mmHg

Note that other liquids can be used instead of mercury in a barometer, but the height in the tube will be inversely proportional to the density of the liquid. In other words, a liquid with a lower density will rise to a greater height. To convert a height in millimeters of one liquid to a height in millimeters of mercury, use the following equation:

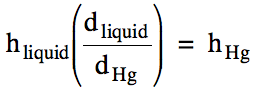
Sample Exercise 5G:

When a barometer containing liquid benzene was used to measure the barometric pressure, the height in the tube was found to be 11.0 meters. Given that the density of liquid benzene is 0.877 g/mL and the density of liquid mercury is 13.6 g/mL, calculate the barometric pressure in atm.

Solution:

The pressure of a gas sample can be measured in the laboratory using a manometer. A typical open-end manometer consists of a curved tube containing liquid mercury that is attached to the gas sample on one end and open to the atmosphere on the other end. If the mercury level in the arm attached to the gas is the same and the mercury level in the arm open to the atmosphere, then P_gas = P_bar. However, if the mercury level in the arm attached to the gas is lower than the mercury level in the arm open to the atmosphere, then P_gas = P_bar + h, where h is the difference in heights between the mercury levels in the two arms:

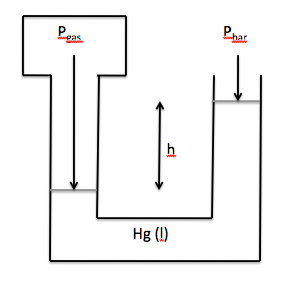
If the mercury level in the arm attached to the gas is higher than the mercury level in the arm open to the atmosphere, then P_gas = P_bar - h:

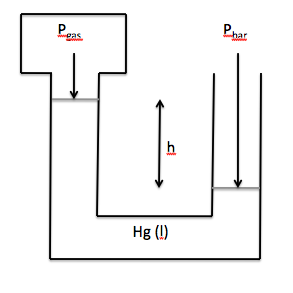
Note that P_bar and h must be in the same unit before h is added to or subtracted from P_bar:

Sample Exercise 5H:

On a day when the barometric pressure was 0.967 atm, the pressure of a gas sample was measured using an open-end manometer. If the mercury level in the arm attached to the gas was 3.1 centimeters lower than the mercury level in the arm open to the atmosphere, calculate the pressure of the gas in torr.

Solution:

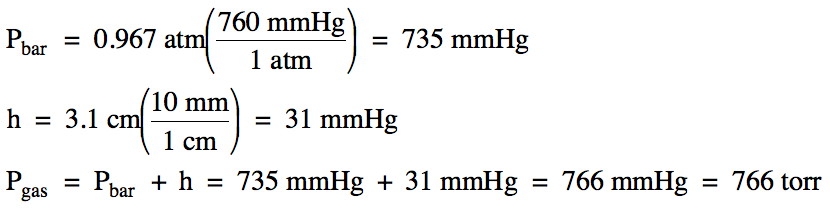
Section 5-6: Collecting Gases Over Water

If we wish to collect the gas produced in a chemical reaction without any escaping, one strategy is to ensure that all the gas is released under water where it will rapidly rise straight up because of the much lower density of the gas relative to the density of water. If a eudiometer (gas-measuring tube with volume markings that is closed on one end and open on the other) is completely filled with water and then inverted into a beaker of water, gas from a chemical reaction that is released inside the opening of the tube will rise straight up and displace water from the tube. Thus, the gas produced will now be trapped in the tube. The tube can usually be adjusted so that the water levels inside and outside the tube are the same, as shown below:

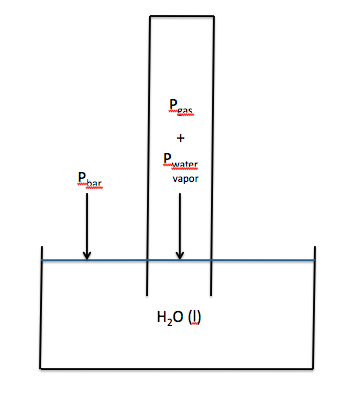
The volume of gas collected can be determined by reading the volume markings on the eudiometer. Since the gas produced must travel through the water before being collected over water, we can use a thermometer to measure the temperature of the water and assume that the temperature of the gas is the same. Note that a gas collected over water will be mixed with water vapor. As such, if the water levels inside and outside the tube are the same, then the following will be true:

P_bar = P_gas + P_water_vapor

The water vapor pressure, which will vary at different temperatures and can typically be found on a data table, can be subtracted from the barometric pressure to obtain the partial pressure of the gas:

P_gas = P_bar - P_water_vapor

Once we know the pressure, volume, and temperature of the gas, we can calculate the moles of gas produced in the chemical reaction, after which stoichiometry can be used to find the mass of one of the reactants used:

Sample Exercise 5I:

On a day when the barometric pressure was 749 mmHg, oxygen gas was produced in the following unbalanced decomposition reaction:

KClO₃ (s) → KCl (s) + O₂ (g)

The oxygen gas was collected over water at 25°C (water vapor pressure at 25°C = 24 mmHg). If 264 mL of oxygen gas was collected, calculate the mass of KClO₃ decomposed in the reaction.

Solution:

We first subtract to find the partial pressure of the oxygen gas and then use the Ideal Gas Law to find the moles of oxygen gas produced, after which we use the stoichiometry of the balanced equation to determine the mass of KClO₃ decomposed:

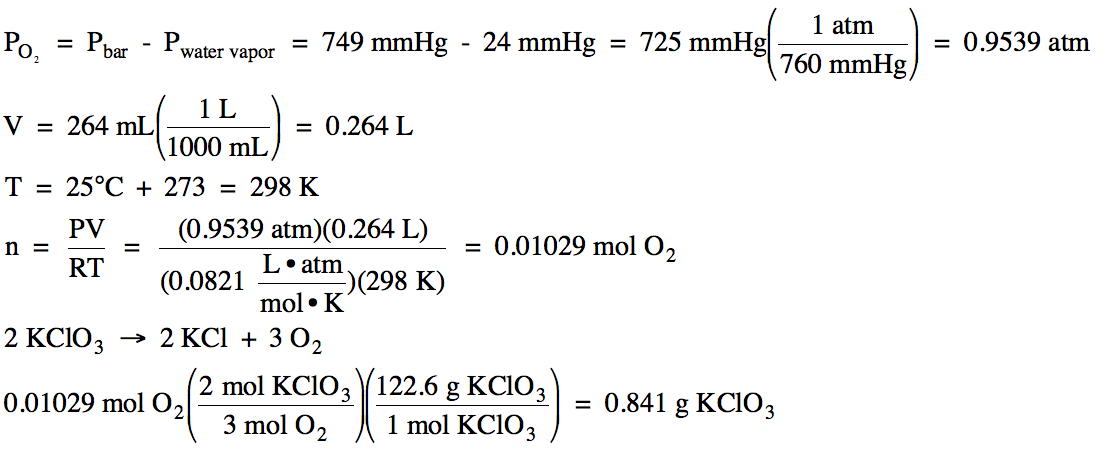
Section 5-7: Experiment – Determining the Gas Constant R

The value of the gas constant R can be determined experimentally after collecting a gas over water. In some cases, it may not be possible to adjust the tube in order to equalize the water levels inside and outside. As such, the water level inside the tube may be higher than the water level outside, as shown below:

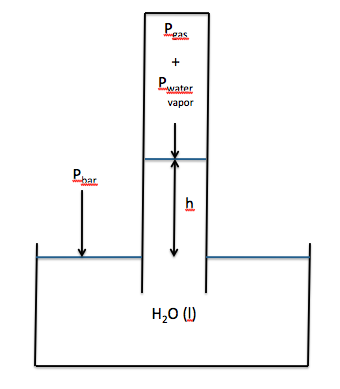
If the water level inside the tube is higher than the water level outside, then the following will be true:

P_bar = P_gas + P_water_vapor + h

Therefore, the partial pressure of the gas can be calculated as follows:

P_gas = P_bar - P_water_vapor - h

Note that h must be converted from millimeters of water to millimeters of mercury before being subtracted:

Sample Exercise 5J:

In an experiment to determine the value of the gas constant R, hydrogen gas was collected over water after being produced in the following unbalanced reaction:

Al (s) + HBr (aq) → H₂ (g) + AlBr₃ (aq)

The water level inside the tube was higher than the water level outside, and the following data was recorded:

mass of aluminum reacted	0.0273 g
volume of gas collected	38.17 mL
temperature of water	23°C
water vapor pressure at 23°C	21.1 mmHg
barometric pressure	758.4 mmHg
difference in water levels (h)	14.2 cm H₂O

Given that the density of water is 1.00 g/mL and the density of mercury is 13.6 g/mL, calculate the experimentally determined value of R with units to the correct number of significant figures.

Solution:

First, we must convert h to mmHg before subtracting to obtain the partial pressure of the hydrogen gas. We then can use the mass of aluminum reacted and the stoichiometry of the balanced equation to calculate the moles of hydrogen gas, after which we can use the Ideal Gas Law to calculate the experimentally determined value of R:

Section 5-8: Graham’s Law

Effusion is the escape of gas molecules through a tiny opening in the container. Graham’s Law essentially states that the effusion rate (r) of a gas will be inversely proportional to the square root of the molar mass of the gas. Alternatively, Graham’s Law can be expressed through the equation below for two different gases A and B:

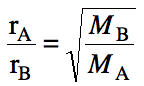
We can also determine the ratio of effusion distances (d) or moles (n) effused in a certain time period as follows:

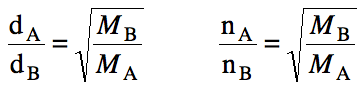
Since gases with larger molar masses will take longer to effuse, we can determine the ratio of effusion times (t) as follows:

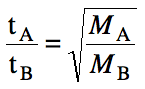
Sample Exercise 5K:

A sample of neon gas requires 158 seconds to effuse from a container. How long would an equivalent sample of argon gas take to effuse under identical conditions?

Solution:

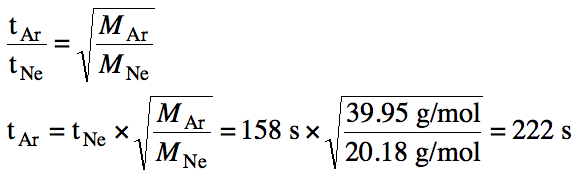
Chapter 5 Practice Exercises and Review Quizzes:

5-1) A 0.153 g sample of carbon dioxide gas occupies a volume of 84.0 mL at 777 mmHg. What is the temperature of the carbon dioxide in °C?

Click for Solution

5-1)

5-2) Given the unbalanced equation below for the decomposition of nitroglycerin, if 6.0 kilograms of solid C₃H₅(NO₃)₃ decompose, what volume of nitrogen gas will be produced at STP?

C₃H₅(NO₃)₃ (s) → CO₂ (g) + H₂O (g) + N₂ (g) + O₂ (g)

Click for Solution

5-2)

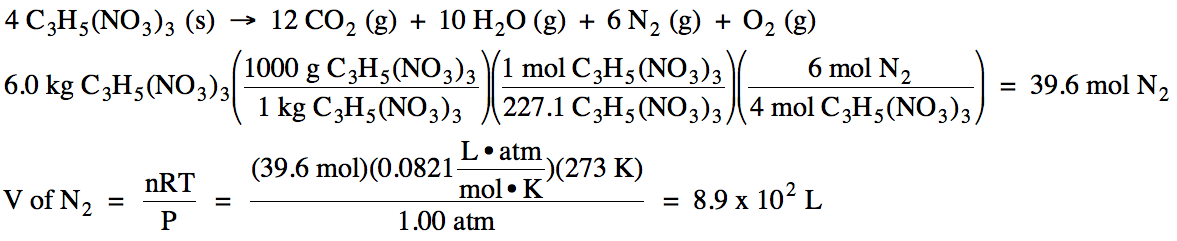
5-3) Given the unbalanced equation below, if 8.20 grams of solid ZnS is mixed with 2.93 grams of oxygen gas:

(a) Which is the limiting reagent?

(b) What maximum volume of SO₂ gas can form at 26°C and 717 torr?

ZnS (s) + O₂ (g) → ZnO (s) + SO₂ (g)

Click for Solution

5-3)

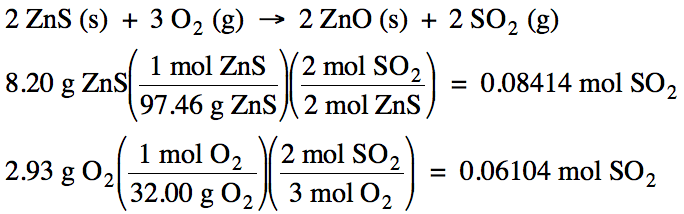
(a) O₂ produces less SO₂, so O₂ is the limiting reagent.

(b)

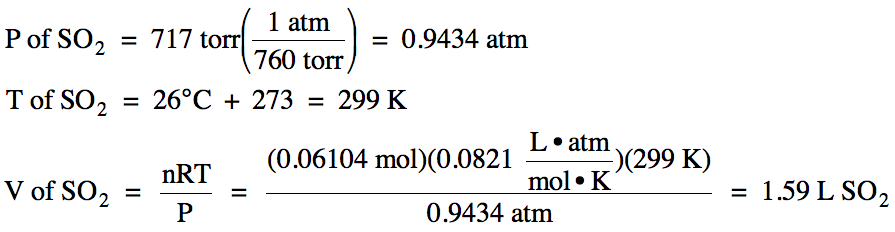
(c)

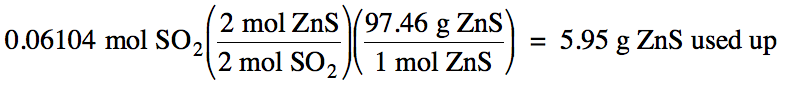
8.20 g – 5.95 g = 2.25 g ZnS excess

5-4) Given the unbalanced equation below, if 95 mL of CO gas, measured at 55°C and 794 mmHg, reacts with an excess of solid nickel and then 0.050 grams of Ni(CO)₄ is actually collected, what is the percent yield of the reaction?

Ni (s) + CO (g) → Ni(CO)₄ (g)

Click for Solution

5-4)

5-5) (a) An unknown gas was found to be 64.24% carbon and 10.78% hydrogen by mass, with the remainder being nitrogen. Determine the empirical formula of the compound.

(b) In a separate experiment, a 10.1 gram sample of the gas was found to occupy 4.80 L at 525°C and 936 torr. Determine the molar mass and molecular formula of the unknown gas.

Click for Solution

5-5) (a) 100% - 64.24% C – 10.78% H = 24.98% N by mass

Assume one hundred grams of unknown compound:

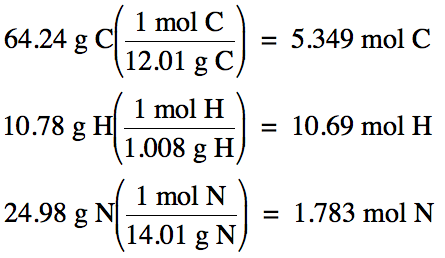
5.349 mol C: 10.69 mol H: 1.783 mol N (divide each by 1.783)

= 3 mol C: 6 mol H: 1 mol N

Therefore, empirical formula is C₃H₆N.

(b)

5-6) What is the density of Cl₂ gas at STP?

Click for Solution

5-6)

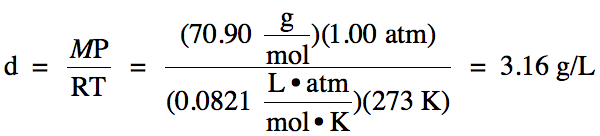
5-7) A sample of gas occupies a volume of 625 mL at 85°C and 705 torr. What will be the new temperature of the gas in °C if the volume is decreased to 500. mL and the pressure in increased to 805 torr?

Click for Solution

5-7)

5-8) A gaseous mixture of 0.170 mol methane and 0.510 mol ethane has a total pressure of 748 mmHg. Calculate the partial pressure of each gas in mmHg.

Click for Solution

5-8)

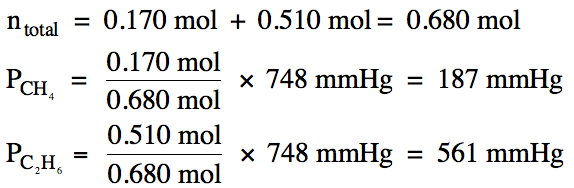
5-9) When a barometer containing liquid glycerol was used to measure the barometric pressure, the height in the tube was found to be 7.58 meters. Given that the density of liquid glycerol is 1.26 g/mL and the density of liquid mercury is 13.6 g/mL, calculate the barometric pressure in atm.

Click for Solution

5-9)

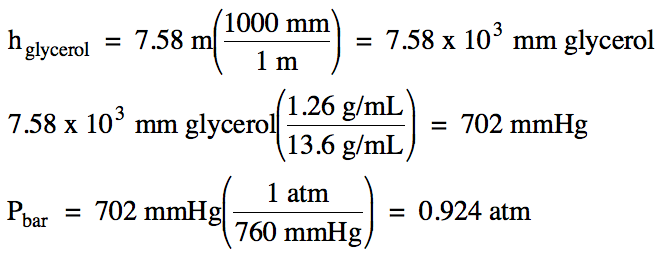
5-10) On a day when the barometric pressure was 1.01 atm, the pressure of a gas sample was measured using an open-end manometer. If the mercury level in the arm attached to the gas was 2.4 centimeters higher than the mercury level in the arm open to the atmosphere, calculate the pressure of the gas in torr.

Click for Solution

5-10)

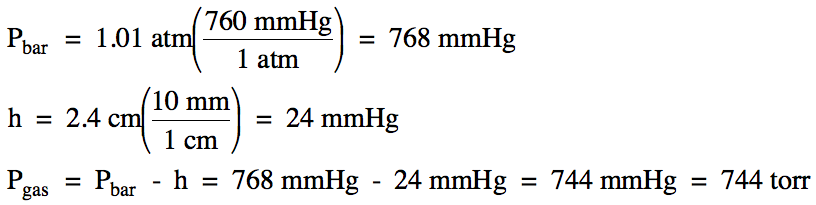
5-11) On a day when the barometric pressure was 769 mmHg, hydrogen gas was produced in the following unbalanced reaction:

K (s) + H₂O (l) → KOH (aq) + H₂ (g)

The hydrogen gas was collected over water at 35°C (water vapor pressure at 35°C = 42 mmHg). If 491 mL of hydrogen gas was collected, calculate the mass of solid potassium metal that reacted.

Click for Solution

5-11)

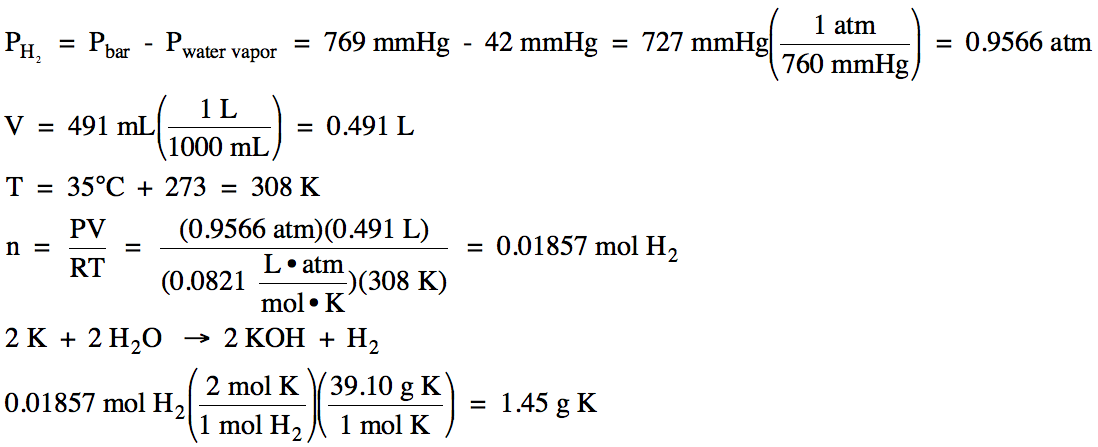
5-12) In an experiment to determine the value of the gas constant R, oxygen gas was collected over water after being produced in the following unbalanced reaction:

H₂O₂ (l) → O₂ (g) + H₂O (l)

The water level inside the tube was higher than the water level outside, and the following data was recorded:

mass of H₂O₂ reacted	0.108 g
volume of gas collected	40.19 mL
temperature of water	19°C
water vapor pressure at 19°C	16.5 mmHg
barometric pressure	764.2 mmHg
difference in water levels (h)	15.8 cm H₂O

Given that the density of water is 1.00 g/mL and the density of mercury is 13.6 g/mL, calculate the experimentally determined value of R with units to the correct number of significant figures.

Click for Solution

5-12)

5-13) A 4.8 gram sample of a solid mixture contains KHCO₃ as well as unreactive material. When heated, only the KHCO₃ in the mixture decomposes to produce 574 mL of carbon dioxide gas at 115°C and 718 torr according to the following unbalanced equation:

KHCO₃ (s) → K₂CO₃ (s) + H₂O (g) + CO₂ (g)

What is the percent by mass of KHCO₃ in the mixture?

Click for Solution

5-13)

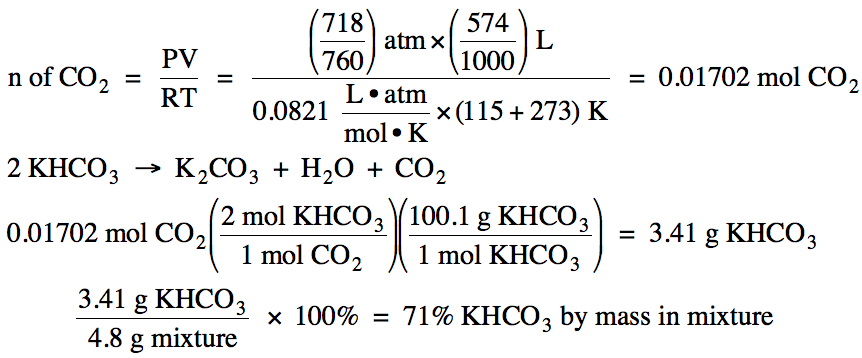
5-14) A sample of N₂ gas effuses 675 millimeters from a container. How far would an equivalent sample of CH₄ gas effuse under identical conditions?

Click for Solution

5-14)

Click for Review Quiz 1

Click for Review Quiz 1 Answers