Chapter 1: Converting Units and Rounding Answers

Section 1-1: Converting Units Using Dimensional Analysis

Section 1-5: Experiment - Determining the Density of a Solid by Water Displacement

Chapter 1 Practice Exercises and Review Quizzes

Section 1-1: Converting Units Using Dimensional Analysis

In life and in the chemistry laboratory, you may find yourself taking a measurement in one particular unit, but then needing to express your measurement in a different unit. The simple problem below will demonstrate a systematic written approach to unit conversion known as Dimensional Analysis:

Sample Exercise 1A:

A penalty kick in soccer is taken from a distance of 36 feet to the goal. How many yards from the goal is this distance?

Solution:

We begin by noting the conversion factor to be used:

1 yard (yd) = 3 feet (ft)

We then multiply the original measurement by the conversion factor expressed as a fraction in parentheses with the desired unit in the numerator and the original unit in the denominator:

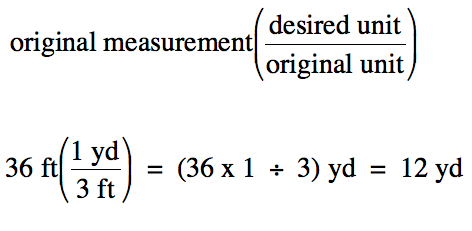
Note that the unit "ft" appears in both the numerator and the denominator of the above calculation and, thus, cancels out of the final answer.

Dimensional analysis may require using two or more consecutive conversion factors, as shown in the following problem:

Sample Exercise 1B:

A cross-country trip took a total of 3600 minutes. How many days did this trip take?

Solution:

We begin by outlining a multi-step strategy to convert from the original to the desired unit:

minutes (min) → hours (hr) → days (d)

We then note the necessary conversion factors in order and use them consecutively:

1 hr = 60 min

1 d = 24 hr

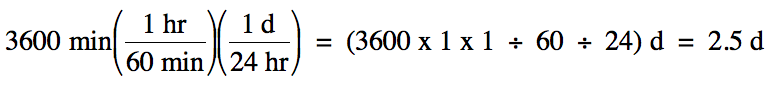
Note that it was not necessary to stop and actually calculate the number of hours along the way to finding the final answer in days.

Typical chemistry lab equipment provides measurements with International System (SI) units that essentially follow the metric system and utilize the following common prefixes to scale up to larger units or down to smaller units:

Prefix	Multiply Unit By
kilo (k)	1000
centi (c)	1/100
milli (m)	1/1000

Here are some common conversion factors to help you convert between the customary U.S. units that you may encounter in your daily life and SI units:

Measurement	U.S. Unit	SI Unit
Distance/Length	1 inch (in)	2.54 centimeters (cm)
Energy	1 calorie (cal)	4.18 joules (J)
Mass	1 pound (lb)	454 grams (g)
Volume	1 gallon (gal)	3.79 liters (L)

Section 1-2: Significant Figures

The number of significant figures (sig. fig.s) in a measurement is essentially an indication of how precise the measurement is. A measurement reported with more sig. fig.s is considered to have less uncertainty.

Use the following rules to determine the number of sig. fig.s in a measurement:

1. All non-zero digits count as sig. fig.s. For example:

48 = 2 sig. fig.s

25.7 = 3 sig. fig.s

2. All zeros between non-zero digits count as sig. fig.s. For example:

102 = 3 sig. fig.s

7060.09 = 6 sig. fig.s

3. For measurements less than 1, all zeros after the decimal point and to the right of the last non-zero digit count as sig. fig.s, but all zeros to the left of the first non-zero digit do not count as sig. fig.s. For example:

0.40 = 2 sig. fig.s

0.00080200 = 5 sig. fig.s

0.00009 = 1 sig. fig.

6.070 x 10^-3 = 4 sig. fig.s

4. For measurements greater than or equal to 1 with a decimal point shown, all zeros count as sig. fig.s. For example:

1.00 = 3 sig. fig.s

220.0 = 4 sig. fig.s

56,000. = 5 sig. fig.s

5. For measurements greater than or equal to 1 with no decimal point shown, the number of sig. fig.s can be ambiguous. To avoid ambiguity, it is best to use scientific notation in order to be clear about the number of sig. fig.s intended. For example:

30,200 = ??? sig. fig.s

3.02 x 10⁴ = 3 sig. fig.s

3.020 x 10⁴ = 4 sig. fig.s

3.0200 x 10⁴ = 5 sig. fig.s

Section 1-3: Rounding Answers

As we perform calculations throughout this textbook, we will generally round answers according to the following rules:

1. For problems where only 1 measurement is given, round the final answer to the same number of sig. fig.s as the original measurement.

Sample Exercise 1C:

Convert the following measurements:

(a) 0.030 miles (mi) to centimeters

(b) 20.0 milliliters to gallons

Solution:

(a) strategy: mi → ft → in → cm

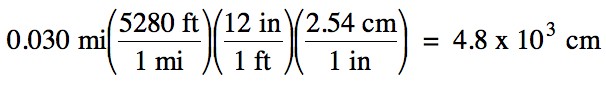
Since the original measurement 0.030 has 2 sig. fig.s, we should round the calculated answer of 4828 down to 2 sig. fig.s using scientific notation to avoid ambiguity.

(b) strategy: mL → L → gal

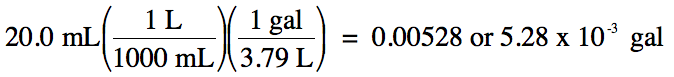
Since the original measurement 20.0 has 3 sig. fig.s, we must round up the calculated answer of 0.005277 up to 3 sig. fig.s. In this case, whether or not to use scientific notation is a matter of preference as long as the final answer has 3 sig. fig.s.

2. For problems that combine addition or subtraction with multiplication or division, always perform all the addition or subtraction steps first before proceeding to the multiplication or division steps.

3. When two or more measurements are added or subtracted, round the answer to the same number of decimal places (NOT sig. fig.s!!!) as the measurement with the fewest number of decimal places. For example:

9.8 (1 decimal place) + 0.35 (2 decimal places)

= {calculator says 10.15} = 10.2 (1 decimal place)

10.67 (2 decimal places) – 0.8700 (4 decimal places)

= 9.80 (2 decimal places)

4. When two or more measurements are multiplied or divided, round the answer to the same number of sig. fig.s (NOT decimal places!!!) as the measurement with the fewest number of sig. fig.s. For example:

0.09000 (4 sig. fig.s) x 8.0 (2 sig. fig.s) x 12.0 (3 sig. fig.s)

= 0.060 (2 sig. fig.s)

Note that for longer problems throughout the textbook, it is acceptable and often preferred to keep an extra sig. fig. for each intermediate calculation as long as the final answer is rounded to the proper number of sig. fig.s.

Section 1-4: Density

Density is the ratio of the mass of a substance to the volume of space the substance occupies:

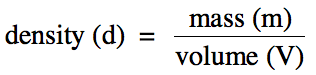
The densities of laboratory chemicals are typically expressed in the SI unit g/cm³ or the equivalent g/mL. (Note, however, that the density unit g/mL is not used for solids.)

Sample Exercise 1D:

A 41.1 g piece of iron metal is found to occupy a volume of 5.2 cm³. What is the density of the iron metal?

Solution:

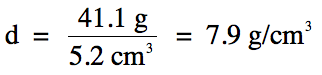
Note that since we are dividing 41.1 (3 sig. fig.s) by 5.2 (2 sig. fig.s), the final answer should be rounded to 2 sig. fig.s.

The density equation above can be rearranged to solve for either mass or volume:

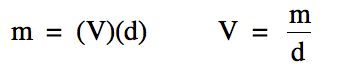
When finding mass or volume, rather than plugging the measurements given in the problem into one of the two equations above, we will instead use dimensional analysis with density as a conversion factor between mass and volume as demonstrated in the following two problems:

Sample Exercise 1E:

Liquid mercury has a density of 13.6 g/mL. What is the mass of 7.2 mL of liquid mercury?

Solution:

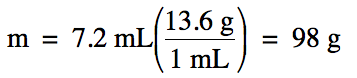
Sample Exercise 1F:

Table salt has a density of 2.2 g/cm³. What is the volume of 75.5 g of table salt?

Solution:

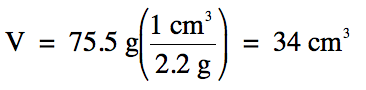
We can convert between volumes in m³ and cm³ by cubing both sides of the known conversion factor as follows:

1 m = 100 cm

(1 m)³ = (100 cm)³

1 m³ = 100³ cm³

The use of the volume conversion factor derived above in dimensional analysis will be demonstrated at the end of the chapter in Practice Exercise 1-3.

Section 1-5: Experiment – Determining the Density of a Solid by Water Displacement

The density of a solid can be determined in a lab using a simple method known as water displacement that follows the procedure below:

1) Record the mass of the solid.

2) Partially fill a graduated cylinder with water and record the initial volume of the water.

3) Carefully add the solid to the graduated cylinder to avoid water splashing out and then record the final volume of the water and solid combined.

4) Subtract to find the volume of the solid and then calculate the density of the solid.

Sample Exercise 1G:

In an experiment to determine the density of a solid by water displacement, a student recorded the following data:

Mass of Solid	19.21 g
Initial Volume of Water	14.2 mL
Final Volume of Water + Solid	15.9 mL

Based on the experimental data above, what is the correctly-rounded density of the solid?

Solution:

[Recall from Section 1-3 that we always perform all the addition and subtraction steps first using the fewest decimal places rounding rule followed by the multiplication and division steps using the fewest sig. fig.s rounding rule. As a result, it is possible for the final answer to not have the same number of sig. fig.s as any of the original measurements given in the problem.]

First, subtract to find the volume of the solid, but then change the unit from mL to the equivalent cm³ because mL is not used for the volume of solids:

15.9 mL – 14.2 mL = 1.7 mL = 1.7 cm³

Note that since both measurements in the above subtraction step have 1 decimal place, the calculated volume should have 1 decimal place.

Now simply divide mass by volume to find density:

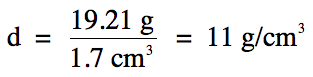
Note that we have now switched over to the fewest sig. fig.s rounding rule for the above division step. As such, the final answer should have 2 sig. fig.s because the calculated volume of the solid has 2 sig. fig.s.

Note also that the calculated density may differ from the true value due to experimental error. For example, if water splashes out of the graduated cylinder as the solid is added, the final volume recorded will be too low. As a result, the volume of the solid found by subtraction will be too low, leading to an erroneously high density.

Chapter 1 Practice Exercises and Review Quizzes:

1-1) How many significant figures are in each of the following:

(a) 0.00002030

(b) 670.

Click for Solution

1-1) (a) 0.00002030 = 4 sig. fig.s

(b) 670. = 3 sig. fig.s

1-2) Convert the following measurements:

(a) 0.0070 pounds to milligrams

(b) 0.0900 gallons to milliliters

Click for Solution

1-2)

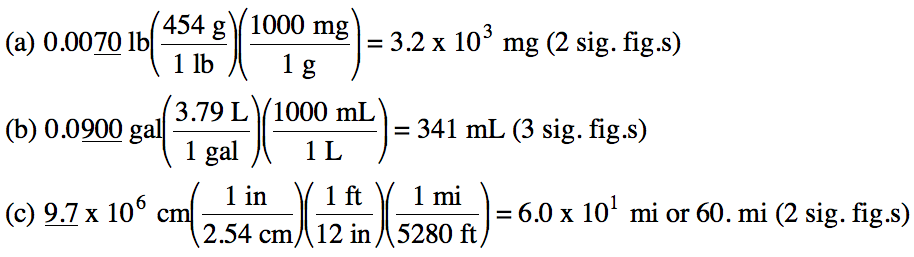
1-3) The density of aluminum metal is 2.72 g/cm³. What is the mass in milligrams of 0.36 m³ of aluminum metal?

Click for Solution

1-3)

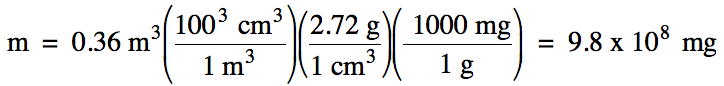
Note that we should use scientific notation and round our calculated answer of 9.79 x 10⁸ up to obtain 2 sig. fig.s because the volume given in the problem has 2 sig. fig.s.

1-4) The density of liquid ethanol is 0.79 g/mL. What is the volume in gallons of 0.0475 kilograms of ethanol?

Click for Solution

1-4)

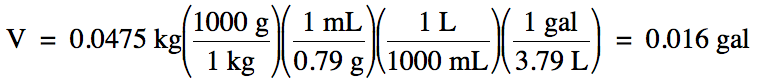
Note that we should round our calculated answer of 0.0159 up to obtain 2 sig. fig.s because the density given in the problem has 2 sig. fig.s.

1-5) In an experiment to determine the density of a solid by water displacement, a student recorded the following data:

Mass of Solid	17.2 g
Initial Volume of Water	11.3 mL
Final Volume of Water + Solid	12.1 mL

Based on the experimental data above, what is the correctly-rounded density of the solid?

Click for Solution

1-5)

12.1 mL – 11.3 mL = 0.8 mL = 0.8 cm³

(subtraction = round to 1 decimal place)

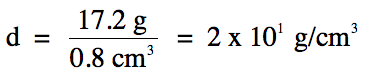
Note that we switch over to the fewest sig. fig.s rounding rule for the division step, so we should round our calculated answer of 21.5 down to 1 sig. fig. using scientific notation because the calculated volume has 1 sig. fig.

Click for Review Quiz 1

Click for Review Quiz 1 Answers