Chapter 11: Molecular Geometry, Polarity of Molecules, and Advanced Bonding Theory

Section 11-1: Molecular Geometry: Using VSEPR Theory to Determine Three-Dimensional Shapes and Bond Angles

Section 11-5: Molecular Orbital (MO) Theory

Chapter 11 Practice Exercises and Review Quizzes

Section 11-1: Molecular Geometry: Using VSEPR Theory to Determine Three-Dimensional Shapes and Bond Angles

Diatomic molecules and ions are linear, regardless of the number of covalent bonds between the atoms. For molecules or ions with three or more bonded atoms, the Lewis structure indicates which specific atoms are bonded together and the number of bonds between the atoms. However, the Lewis structure does not necessarily provide an accurate depiction of the three-dimensional shape and bond angles in the molecule or ion.

Valence-Shell Electron-Pair Repulsion (VSEPR) Theory suggests that the valence electron domains comprised of covalent bonds and lone pairs adjacent to the central atom in a molecule or ion will be arranged in a three-dimensional shape that minimizes electron repulsion between the bonds and lone pairs. We will use the VSEPR notation AB_xE_y to categorize molecules and ions, where A represents the center atom, x represents the number of outer atoms (B) bonded to the center atom A, and y represents the number of lone pairs (E) on the center atom A. Once we know the VSEPR notation for an atom or ion, we can determine the three-dimensional shape and bond angles. When we draw three-dimensional sketches of molecules or ions on paper, we will use solid straight lines to represent bonds oriented in the plane of the paper, dashed wedges to represent bonds oriented back behind the plane of the paper, and solid wedges to represent bonds oriented forward out of the paper. We will also only include lone pairs on the center atom in sketches, but not lone pairs on the outer atoms as these generally do not affect the shape according to VSEPR Theory:

I. AB₂E₀ = AB₂ = two outer atoms bonded to center atom + no lone pairs on center atom = molecule is linear:

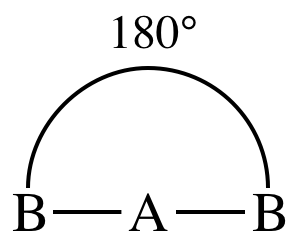
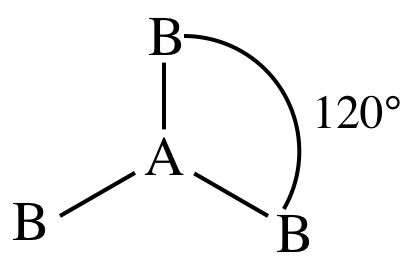
II. AB₃E₀ = AB₃ = three outer atoms bonded to center atom + no lone pairs on center atom = molecule is trigonal planar:

III. AB₂E₁ = two outer atoms bonded to center atom + one lone pair on center atom = molecule is bent:

The bond angle is decreased below 120° because the lone pair has a slightly greater repulsive effect than the electrons in the covalent bonds between A and B.

IV. AB₄E₀ = AB₄ = four outer atoms bonded to center atom + no lone pairs on center atom = tetrahedral:

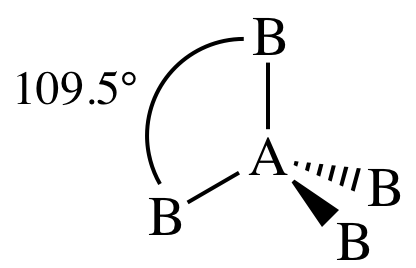
V. AB₃E₁ = three outer atoms bonded to center atom + one lone pair on center atom = trigonal pyramidal:

The bond angles are decreased below 109.5° because the lone pair has a slightly greater repulsive effect than the electrons in the covalent bonds between A and B.

VI. AB₂E₂ = two outer atoms bonded to center atom + two lone pairs on center atom = bent:

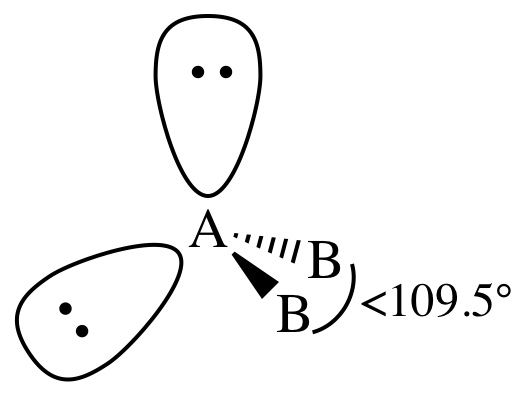
In the AB₂E₂ = bent case, the extra electron repulsion caused by the second lone pair on the center atom may cause the B-A-B bond angle to decrease even further below 109.5° than the decrease expected in the AB₃E₁ = trigonal pyramidal case with only one lone pair on the center atom.

In contrast to the Lewis structures, our three-dimensional sketches will neglect the differences between and, thus, not distinguish among single, double, and triple bonds, as demonstrated in the following problem:

Sample Exercise 11A:

Draw the Lewis structure, name the molecular geometry (shape), draw a three-dimensional sketch, and indicate the bond angle for each of the following molecules and ions:

(a) CO₂

(b) NH₃

(d) CH₄

(e) NO₂^-

(f) H₂O

Solution:

(a)

Lewis structure:

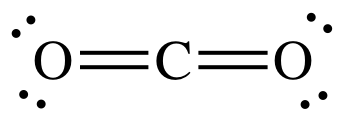
AB₂ = linear

3-D sketch:

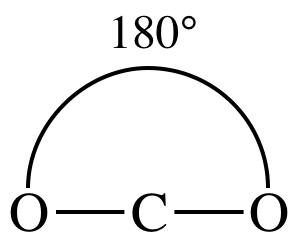
(no need to distinguish between single v. double v. triple bonds in sketch)

(b)

Lewis structure:

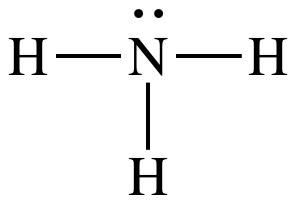
AB₃E₁ = trigonal pyramidal

3-D sketch:

(c)

Lewis structure:

Note that we do not actually need to draw all the resonance structures to determine the shape as we can see from any one of the three resonance structures that the carbonate ion = AB₃ = trigonal planar.

3-D sketch:

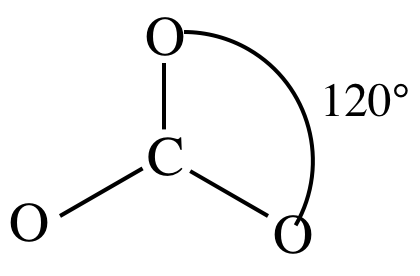
(d)

Lewis structure:

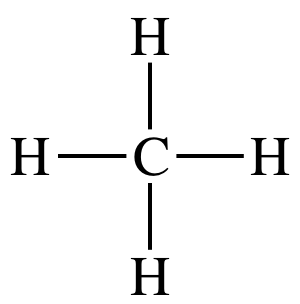
AB₄ = tetrahedral

3-D sketch:

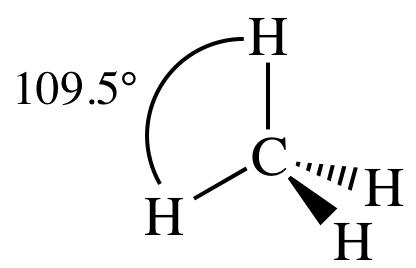
(e)

Lewis structure:

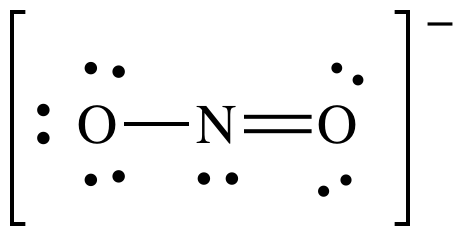
AB₂E₁ = bent (no need to show all resonance structures to determine shape)

3-D sketch:

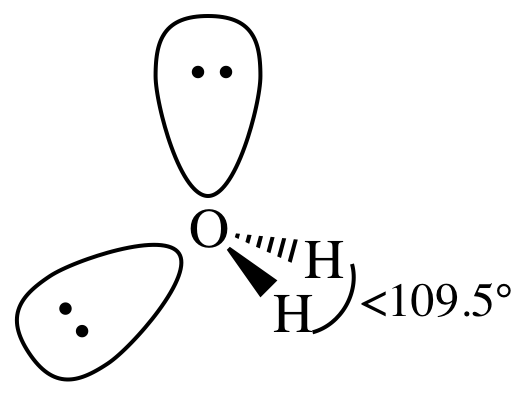
(f)

Lewis structure:

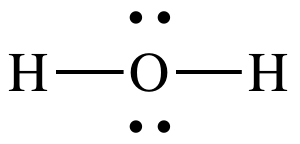
AB₂E₂ = bent

3-D sketch:

For molecules or ions with more than one center atom, we can describe the shape in the region of each center atom as demonstrated in the following problem:

Sample Exercise 11B:

Draw the Lewis structure for acetic acid. Name the molecular geometry and indicate the bond angles in the region of each center atom.

Solution:

Acetic acid = CH₃COOH. All organic acids with the ending COOH have a group of atoms (in this case CH₃) single-bonded to the carbon in the COOH. The carbon in the COOH is double-bonded to one oxygen and single-bonded to the second oxygen, with the hydrogen in the COOH single-bonded to the second oxygen. Therefore, the Lewis structure is:

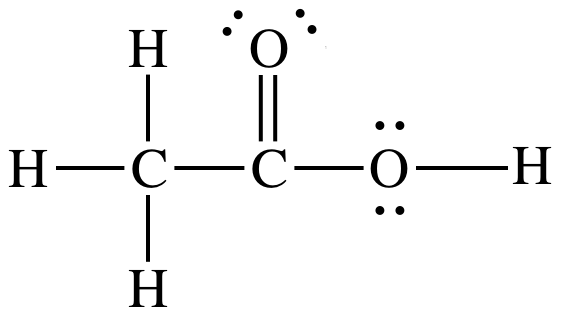
carbon on the left = AB₄ = tetrahedral, bond angles = 109.5°

carbon in center = AB₃ = trigonal planar, bond angles = 120°

oxygen on right = AB₂E₂ = bent, bond angle = <109.5°

For molecules or ions with an “expanded octet” on the center atom, lone pair repulsion will also decrease the bond angle(s), except in the two cases below AB₂E₃ = linear and AB₄E₂= square planar:

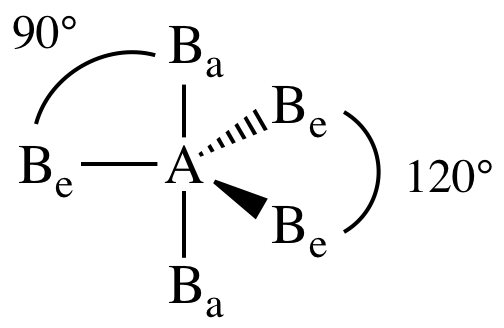
VII. AB₅E₀ = AB₅ = five outer atoms bonded to center atom + no lone pairs on center atom = trigonal bipyramidal. The two outer atoms occupying an axial position (B_a) are not equivalent to the three outer atoms occupying an equatorial position (B_e):

VIII. AB₄E₁ = four outer atoms bonded to center atom + one lone pair on center atom = seesaw. The lone pair must occupy an equatorial position to minimize electron repulsion:

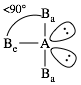
IX. AB₃E₂ = three outer atoms bonded to center atom + two lone pairs on center atom = T-shaped. Both lone pairs must occupy equatorial positions to minimize electron repulsion:

X. AB₂E₃ = two outer atoms bonded to center + three lone pairs on center = linear. All three lone pairs must occupy equatorial positions to minimize electron repulsion:

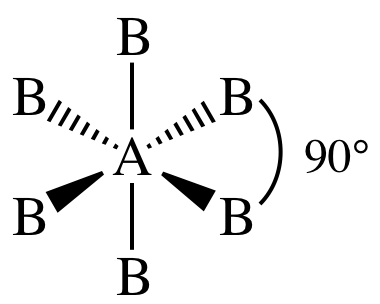
XI. AB₆E₀ = AB₆ = six outer atoms bonded to center + no lone pairs on center = octahedral:

XII. AB₅E₁ = five outer atoms bonded to center + one lone pair on center = square pyramidal:

XIII. AB₄E₂ = four outer atoms bonded to center + two lone pairs on center = square planar:

Sample Exercise 11C:

Draw the Lewis structure, name the molecular geometry (shape), draw a three-dimensional sketch, and indicate the bond angle(s) for each of the following molecules and ions:

(a) BrCl₄^-

(b) BrF₆⁺

(d) IBr₄⁺

(e) PCl₅

(f) SF₃^-

(g) SeCl₅^-

Solution:

(a)

Lewis structure:

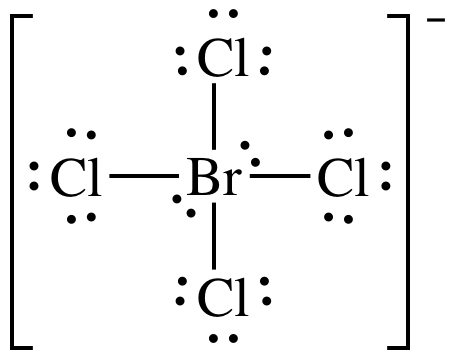
AB₄E₂ = square planar, 3-D sketch:

(b)

Lewis structure:

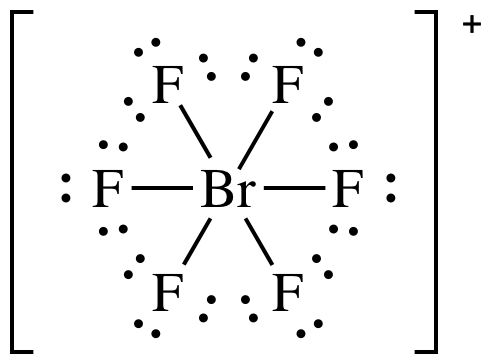
AB₆ = octahedral, 3-D sketch:

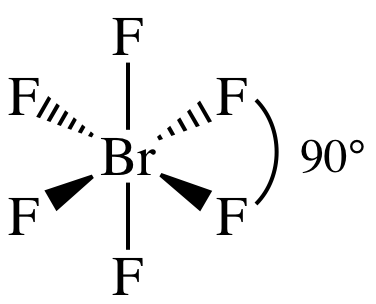
(c)

Lewis structure:

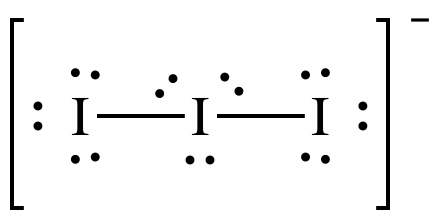
AB₂E₃ = linear, 3-D sketch:

(d)

Lewis structure:

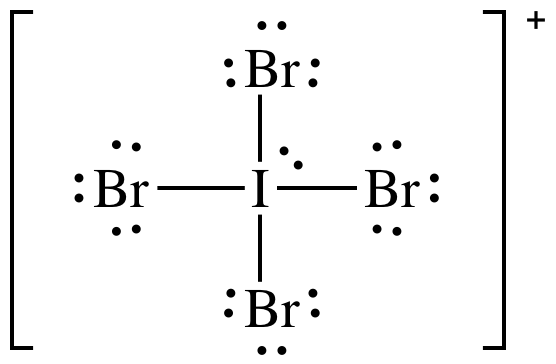
AB₄E₁ = seesaw, 3-D sketch:

(e)

Lewis structure:

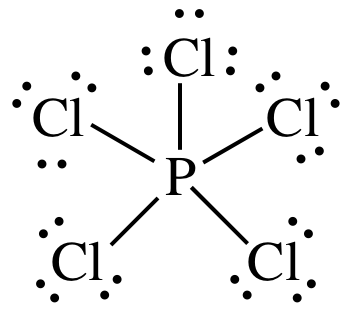
AB₅= trigonal bipyramidal, 3-D sketch:

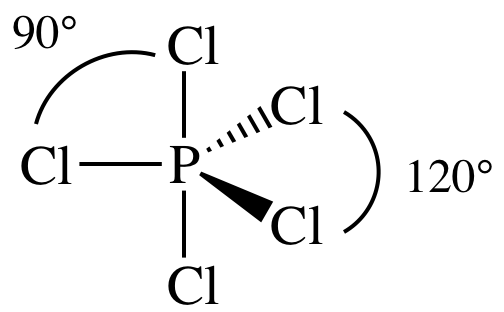
(f)

Lewis structure:

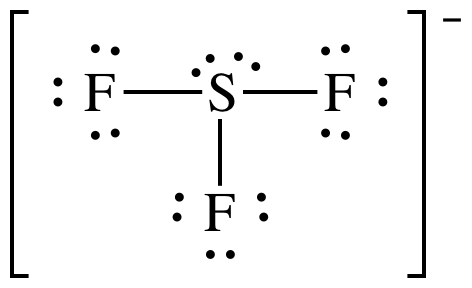
AB₃E₂ = T-shaped, 3-D sketch:

(g)

Lewis structure:

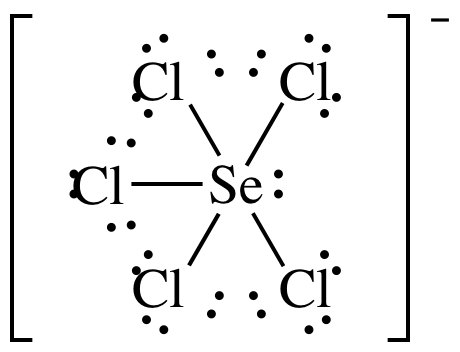
AB₅E₁ = square pyramidal, 3-D sketch:

Section 11-2: Polarity of Molecules

In a polar covalent bond, the electrons will be more attracted toward the more electronegative atom. We can indicate the direction in which the electrons are shifted in a polar covalent bond by placing a bond dipole arrow parallel to the bond in a sketch of the molecule, with the head of the arrow closer to the more electronegative atom and the + end of the arrow closer to the less electronegative atom. For the molecule BrF, the head of the bond dipole arrow will be closer to the more electronegative F atom and the + end of the bond dipole arrow will be closer to the less electronegative Br atom:

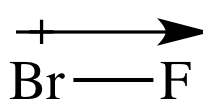
A dipole moment (μ) is essentially a measurement of the overall net shift of electrons toward a particular direction in a neutral molecule. A molecule with no identifiable direction toward which the electrons are shifted is said to be a nonpolar molecule with zero dipole moment (μ = 0). A molecule with an identifiable direction toward which the electrons are shifted is said to be a polar molecule with a dipole moment greater than zero (μ > 0).

In a sketch of the linear carbon dioxide molecule, the heads of the two bond dipole arrows will be closer to the more electronegative outer oxygen atoms:

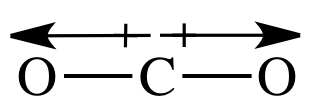
However, since the two bond dipole arrows essentially cancel each other out because they are equal in magnitude but are oriented in opposite directions, carbon dioxide is a nonpolar molecule (μ = 0).

In a sketch of the bent water molecule, the head of the two bond dipole arrows will be closer to the more electronegative center oxygen atom:

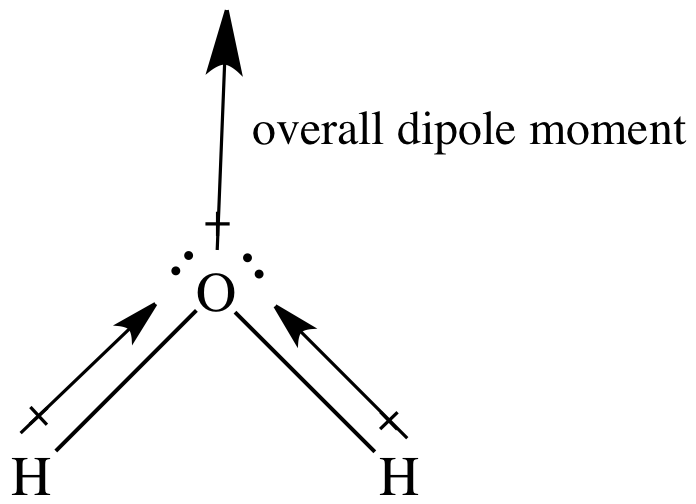
In the case of water, the two bond dipoles arrows are equal in magnitude but do not cancel each other out. We see that there is an overall net shift of electrons and, therefore, a dipole moment oriented toward the oxygen end of the molecule. Thus, water is a polar molecule (μ > 0).

The following general guideline indicates which categories of molecules will be nonpolar and which categories of molecules will be polar:

Molecules with no lone pairs on the center atom will generally be nonpolar if all the outer atoms are the same element. Molecules with one or more lone pairs on the center atom and molecules with outer atoms that are different elements will generally be polar.

For each different category, the table below summarizes the molecular geometry (shape), bond angle, and whether the molecule is polar or nonpolar:

VSEPR Notation	Name of Molecular Geometry (Shape)	Bond Angle	Polar or Nonpolar Molecule?
AB₂	linear	180°	nonpolar*
AB₃	trigonal planar	120°	nonpolar*
AB₂E₁	bent	<120°	polar
AB₄	tetrahedral	109.5°	nonpolar*
AB₃E₁	trigonal pyramidal	<109.5°	polar
AB₂E₂	bent	<109.5°	polar

*unless outer atoms are different elements

Sample Exercise 11D:

Draw the Lewis structure, name the molecular geometry (shape), draw a three-dimensional sketch, indicate the bond angle, and state whether each of the following molecules is polar or nonpolar:

(a) BCl₃

(b) CH₂F₂

(d) SCl₂

(e) PF₃

(f) HNO

Solution:

(a)

Lewis structure:

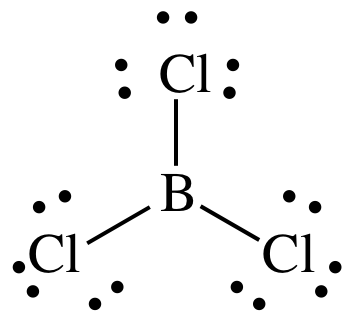
AB₃ = trigonal planar

3-D sketch:

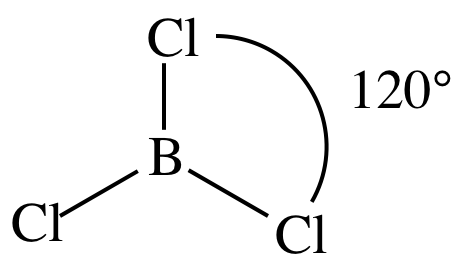
nonpolar molecule

(b)

Lewis structure:

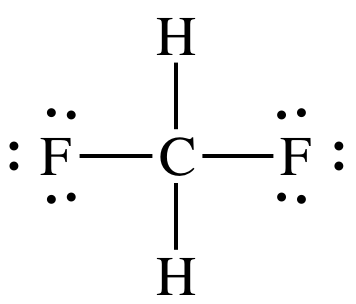
AB₄ = tetrahedral

3-D sketch:

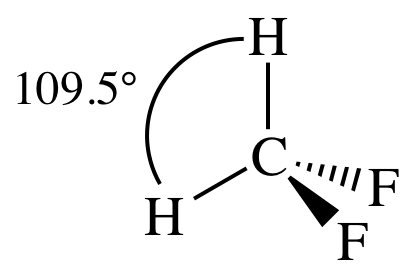
polar molecule (different outer elements)

(c)

Lewis structure:

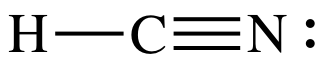
AB₂ = linear

3-D sketch:

polar molecule (different outer elements)

(d)

Lewis structure:

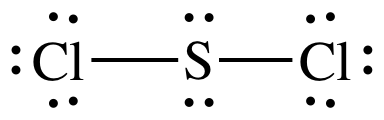
AB₂E₂ = bent

3-D sketch:

polar molecule

(e)

Lewis structure:

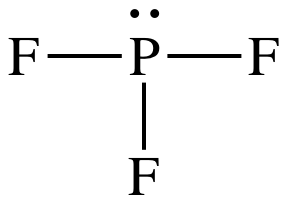
AB₃E₁ = trigonal pyramidal

3-D sketch:

polar molecule

(f)

Lewis structure:

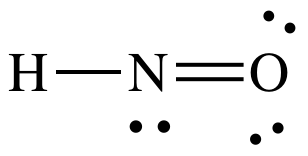
AB₂E₁ = bent

3-D sketch:

polar molecule

For molecules with an “expanded octet” on the center atom, we will focus only on those where all the outer atoms are the same element. Although the general guideline above stating that no lone pairs on center atom = nonpolar molecule and one or more lone pairs on center atom = polar molecule still applies in many cases, note that the orientation of the bonds in AB₂E₃ = linear and AB₄E₂ = square planar molecules results in those molecules being nonpolar.

For each different category of molecules with “expanded octets”, the table below summarizes the molecular geometry (shape), ideal bond angle(s), and whether the molecule is polar or nonpolar:

VSEPR Notation	Name of Molecular Geometry (Shape)	Bond Angle(s)	Polar or Nonpolar Molecule?
AB₅	trigonal bipyramidal	90°, 120°	nonpolar
AB₄E₁	seesaw	<90°, <120°	polar
AB₃E₂	T-shaped	<90°	polar
AB₂E₃	linear	180°	nonpolar
AB₆	octahedral	90°	nonpolar
AB₅E₁	square pyramidal	<90°	polar
AB₄E₂	square planar	90°	nonpolar

Sample Exercise 11E:

Draw the Lewis structure, name the molecular geometry (shape), draw a three-dimensional sketch, indicate the ideal bond angle(s), and state whether each of the following molecules is polar or nonpolar:

(a) AsF₅

(b) BrF₅

(d) KrF₄

(e) SF₄

(f) SeCl₆

(g) XeCl₂

Solution:

(a)

Lewis structure:

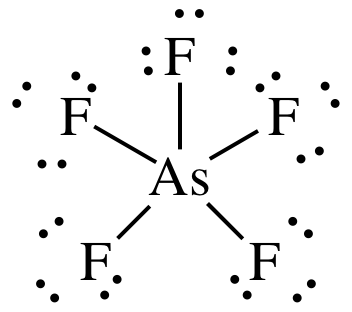
AB₅= trigonal bipyramidal, 3-D sketch:

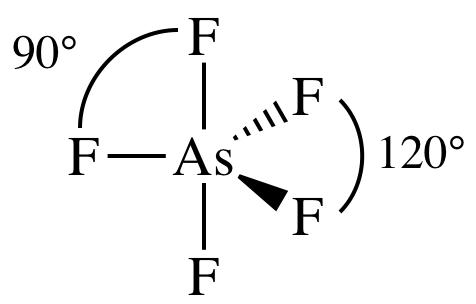
nonpolar molecule

(b)

Lewis structure:

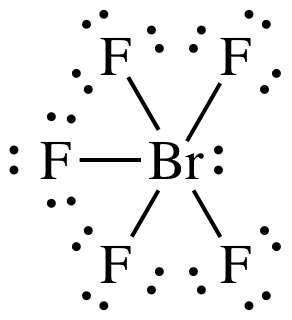
AB₅E₁ = square pyramidal, 3-D sketch:

polar molecule

(c)

Lewis structure:

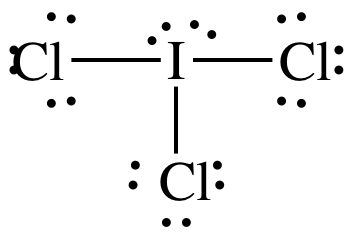
AB₃E₂ = T-shaped, 3-D sketch:

polar molecule

(d)

Lewis structure:

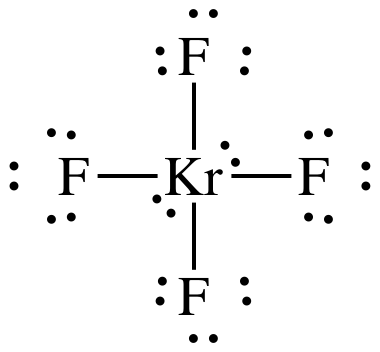
AB₄E₂ = square planar, 3-D sketch:

nonpolar molecule

(e)

Lewis structure:

AB₄E₁ = seesaw, 3-D sketch:

polar molecule

(f)

Lewis structure:

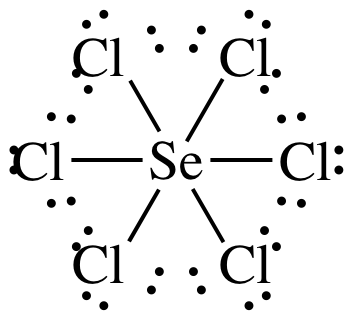
AB₆ = octahedral, 3-D sketch:

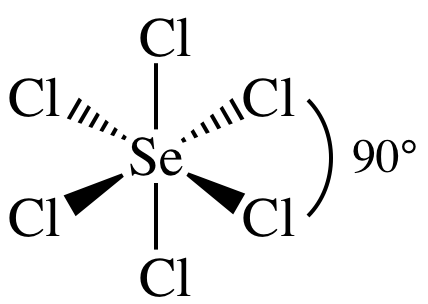
nonpolar molecule

(g)

Lewis structure:

AB₂E₃ = linear, 3-D sketch:

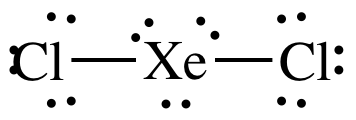
nonpolar molecule

Section 11-3: Hybridization

Valence bond theory generally suggests that a covalent bond is formed when an orbital on one atom occupied by an unpaired valence electron overlaps partially with an orbital on a second atom occupied by an unpaired valence electron. Increased electron density in the region of overlap between the atoms attracts the positively-charged nuclei toward each other.

In some cases, valence bond models depicting overlap between unmodified s and p atomic orbitals would lead to predictions of bond angles and other properties that do not match experimental data. Hybridization theory suggests that the valence s orbital and one or more valence p orbitals from the center atom undergo a change during the bonding process where the original atomic orbitals involved are mixed to create an equivalent number of new hybrid orbitals as follows:

A. If the ideal bond angle in the molecule or ion being formed is 109.5°, one s orbital and three p orbitals from the center atom will mix to create four identical sp³ hybrid orbitals arranged tetrahedrally 109.5° away from each other around the center atom.

B. If the ideal bond angle in the molecule or ion being formed is 120°, one s orbital and two p orbitals from the center atom will mix to create three identical sp² hybrid orbitals arranged in a plane 120° away from each other around the center atom.

C. If the ideal bond angle in the molecule or ion being formed is 180°, one s orbital and one p orbital from the center atom will mix to create two identical sp hybrid orbitals arranged linearly 180° away from each other on opposite sides of the center atom.

The table below summarizes the center atom hybridization based on VSEPR notation:

VSEPR Notation	Center Atom Hybridization
AB₂	sp
AB₃	sp²
AB₂E₁	sp²
AB₄	sp³
AB₃E₁	sp³
AB₂E₂	sp³

Sample Exercise 11F:

Draw the Lewis structure and indicate the center atom hybridization for each of the following molecules and ions:

(a) BrNO

(b) ClCN

Solution:

(a)

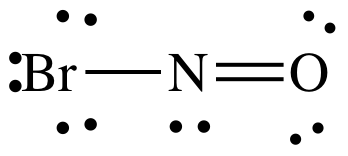
AB₂E₁ = sp²

(b)

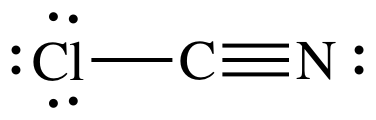
AB₂ = sp

(c)

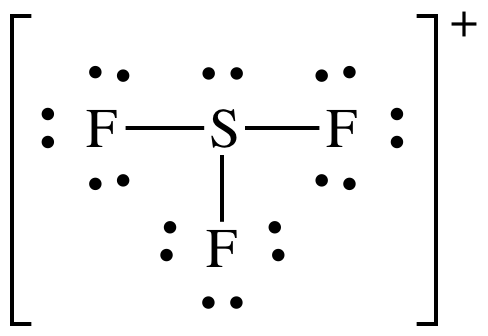
AB₃E₁ = sp³

Section 11-4: Sigma and Pi Bonds

A bond formed as a result of end-to-end overlap of orbitals from two neighboring atoms is known as a sigma (σ) bond. Consider the Lewis structure of C₂H₄:

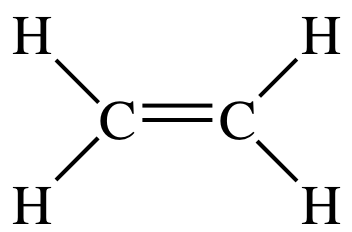
Both carbon atoms in the molecule have three sp² hybrid orbitals (AB₃), each of which is occupied by an unpaired valence electron, that are 120° away from each other in the same plane. A sigma bond will be formed between the carbon atoms as a result of end-to-end overlap between two sp² orbitals, one from each carbon. In addition, sigma bonds will be formed between each hydrogen and a carbon as a result of end-to-end overlap between the 1s orbital occupied by an unpaired valence electron from each hydrogen and an sp² orbital from a carbon. A single bond is always a sigma bond:

single bond = one σ bond

The third valence p orbital on each carbon that was not involved in hybridization will be perpendicular to the plane of the three sp² orbitals. Side-to-side overlap between the parallel p orbitals, each of which is occupied by carbon’s fourth unpaired valence electron that was not used in sigma bonding, results in a second type of bond between the carbons known as a pi (π) bond:

Therefore, a double bond is comprised of one sigma and one pi bond:

double bond = one σ bond + one π bond

Consider the Lewis structure of C₂H₂:

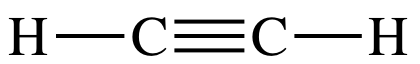
Each carbon atom in the molecule has two sp hybrid orbitals (AB₂), each of which is occupied by an unpaired valence electron, that are 180° away from each other on opposite sides of the carbon. A sigma bond will be formed between the carbon atoms as a result of end-to-end overlap between two sporbitals, one from each carbon. In addition, sigma bonds will be formed between each hydrogen and a carbon as a result of end-to-end overlap between the 1s orbital occupied by an unpaired valence electron from each hydrogen and an sporbital from a carbon.

The other two valence p orbitals on each carbon that were not involved in hybridization will be perpendicular to each other and also to the line of the two sp orbitals. Side-to-side overlap between two pairs of parallel p orbitals, each of which is occupied by one of carbon’s other unpaired valence electrons that was not used in sigma bonding, results in two pi bonds between the carbons:

Therefore, a triple bond is comprised of one sigma and two pi bonds:

triple bond = one σ bond + two π bonds

Sample Exercise 11G:

Draw the Lewis structure for (NH₂)₂CO that has no formal charges and determine the number of sigma and pi bonds in the molecule.

Solution:

6 single + 1 double = 6 sigma + 1 (1 sigma + 1 pi) = 7 sigma bonds + 1 pi bond

Section 11-5: Molecular Orbital (MO) Theory

The Lewis structure shown below suggests that O₂ is diamagnetic because all electrons are paired:

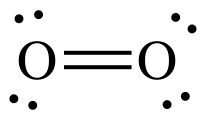
However, we know from experiment that O₂ is, in fact, paramagnetic due to unpaired electrons. Molecular orbital (MO) theory provides an explanation for the paramagnetism of O₂. MO theory suggests that the entire pool of electrons in a molecule occupy a series of molecular orbitals rather than being assigned to orbitals on individual atoms.

For homonuclear (same element) diatomic molecules and ions from the second row of the periodic table, the valence electrons will be assigned to molecular orbitals as follows:

A. When Li, Be, B, C, or N is bonded, the order is: σ_2sσ_2s* π_2p σ_2p π_2p* σ_2p*

B. When O, F, or Ne is bonded, the order is: σ_2s σ_2s* σ_2p π_2p π_2p* σ_2p*

Electrons that occupy bonding molecular orbitals (no asterisk) will strenthen the bond between the atoms, whereas electrons that occupy antibonding molecular orbitals (*) will weaken the bond between the atoms. Sigma (σ) molecular orbitals occur singly and can be occupied by a maximum of two electrons. Pi (π) molecular orbitals occur in pairs, with each orbital occupied by a maximum of two electrons. Therefore, each set of two pi orbitals can be occupied by a maximum of four electrons.

When molecular orbital diagrams are written, two electrons that occupy the same orbital must have opposite spins. Two electrons in a set of pi orbitals must occupy separate orbitals and also must have parallel spins. We can see from the molecular orbital diagram below that O₂ (6 + 6 = 12 valence electrons) will have two unpaired electrons and, therefore, be paramagnetic:

↑↓	↑↓	↑↓	↑↓	↑↓	↑	↑
σ_2s	σ_2s*	σ_2p	π_2p	π_2p	π_2p*	π_2p*	σ_2p*

Bond order in MO theory is analagous to the number of covalent bonds in a Lewis structure. We can determine the bond order for O₂ as follows:

bond order = 0.5(number of bonding electrons – number of antibonding (*) electrons) = 0.5(8–4) = 2

A bond order can be a fraction, and a higher bond order will result in a shorter bond length. For example, O₂⁺ has one less antibonding π_2p* electron than O₂, which gives O₂⁺ a bond order of 0.5(8-3) = 2.5. Since O₂⁺ has a higher bond order than O₂, the bond length of O₂⁺ will be shorter than the bond length of O₂.

Sample Exercise 11H:

(a) Write the molecular orbital diagram for N₂ and determine the bond order. Also state whether N₂ is diamagnetic or paramagnetic.

(b) Is the bond length of N₂^- shorter or longer than the bond length of N₂? Explain.

Solution:

(a) Recall that the π_2p orbitals are filled before the σ_2p orbital when Li, Be, B, C, or N is bonded. An N₂ molecule has 5 + 5 = 10 valence electrons:

↑↓	↑↓	↑↓	↑↓	↑↓
σ_2s	σ_2s*	π_2p	π_2p	σ_2p	π_2p*	π_2p*	σ_2p*

bond order = 0.5(8-2) = 3

no unpaired electrons = diamagnetic

(b) N₂^- has one more antibonding π_2p* electron than N₂, which gives N₂^- a bond order of 0.5(8-3) = 2.5. Since N₂^- has a lower bond order than N₂, N₂^-has a longer bond length than N₂.

If the bond order is determined to be zero, a molecule will not be stable. For example, Ne₂ (8 + 8 = 16 valence electrons) will not be stable:

↑↓	↑↓	↑↓	↑↓	↑↓	↑↓	↑↓	↑↓
σ_2s	σ_2s*	σ_2p	π_2p	π_2p	π_2p*	π_2p*	σ_2p*

bond order = 0.5(8-8) = 0

However, if the molecule is ionized, the resulting ion may be stable. For example, Ne₂⁺ has one less antibonding σ_2p* electron than Ne₂, which gives Ne₂⁺ a bond order of 0.5(8-7) = 0.5. Since the bond order is greater than zero, Ne₂⁺ will be stable.

Chapter 11 Practice Exercises and Review Quizzes:

11-1) Draw the Lewis structure, name the molecular geometry (shape), draw a three-dimensional sketch, and indicate the bond angle for each of the following molecules and ions:

(a) PH₃

(b) NH₂^-

(d) O₃

(e) NH₄⁺

(f) NO₂⁺

Click for Solution

11-1)

(a)

Lewis structure:

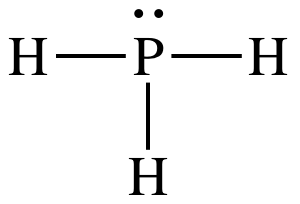
AB₃E₁ = trigonal pyramidal

3-D sketch:

(b)

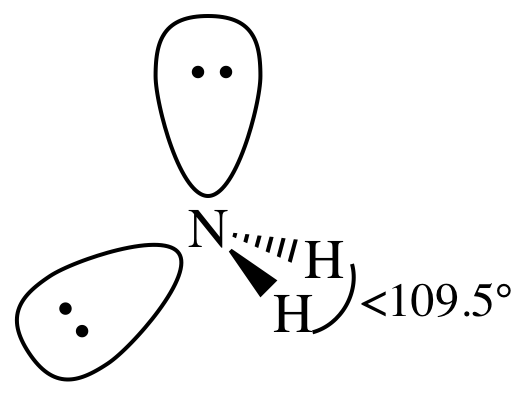
Lewis structure:

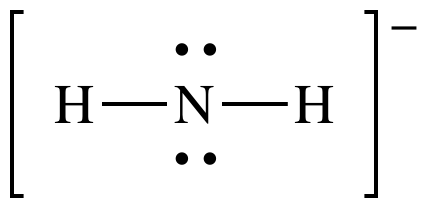
AB₂E₂ = bent

3-D sketch:

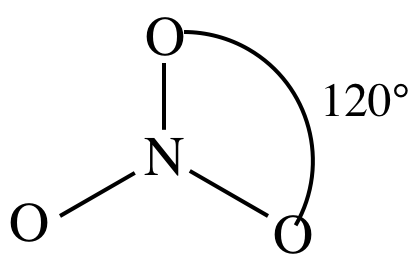
(c)

Lewis structure:

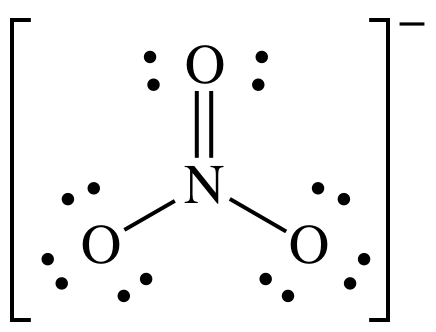
AB₃ = trigonal planar

3-D sketch:

(d)

Lewis structure:

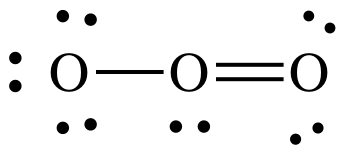
AB₂E₁ = bent

3-D sketch:

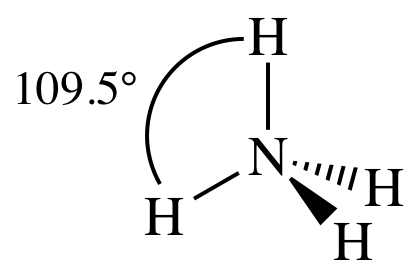
(e)

Lewis structure:

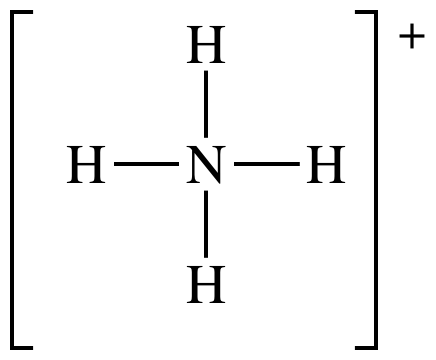
AB₄ = tetrahedral

3-D sketch:

(f)

Lewis structure:

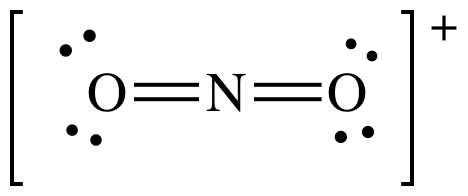
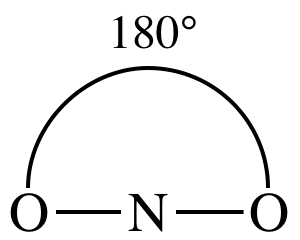
AB₂ = linear

3-D sketch:

11-2) Draw the Lewis structure, name the molecular geometry (shape), draw a three-dimensional sketch, indicate the bond angle, and state whether each of the following molecules is polar or nonpolar:

(a) SiH₄

(b) HOBr

(d) NI₃

(e) ClNO

(f) BF₃

Click for Solution

11-2)

(a)

Lewis structure:

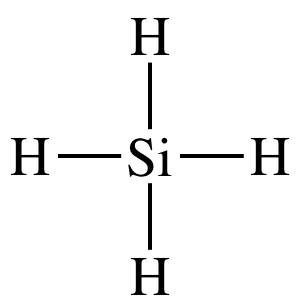
AB₄ = tetrahedral

3-D sketch:

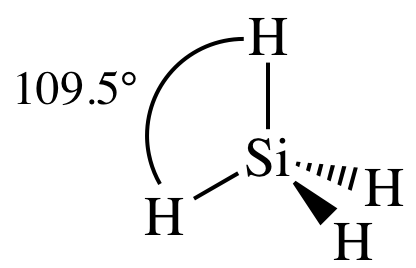
nonpolar molecule

(b)

Lewis structure:

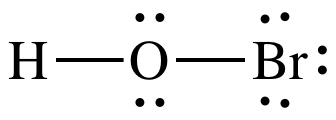
AB₂E₂ = bent

3-D sketch:

polar molecule

(c)

Lewis structure:

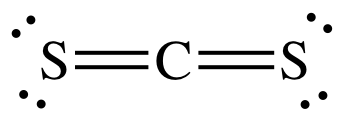
AB₂ = linear

3-D sketch:

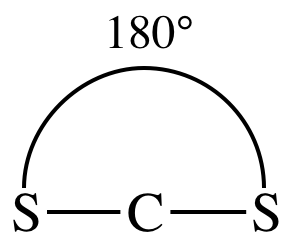
nonpolar molecule

(d)

Lewis structure:

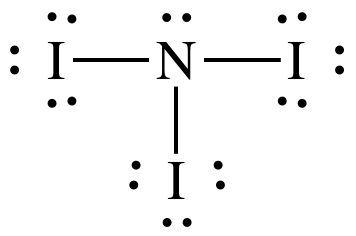
AB₃E₁ = trigonal pyramidal

3-D sketch:

polar molecule

(e)

Lewis structure:

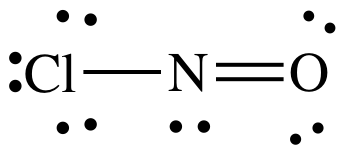
AB₂E₁ = bent

3-D sketch:

polar molecule

(f)

Lewis structure:

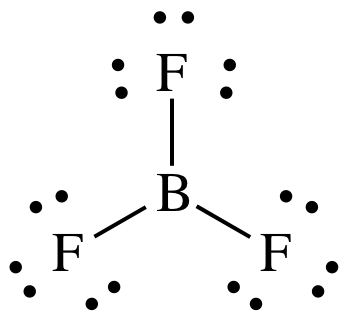
AB₃ = trigonal planar

3-D sketch:

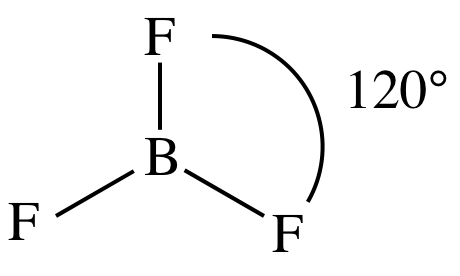
nonpolar molecule

11-3) Draw the Lewis structure, name the molecular geometry (shape), draw a three-dimensional sketch, and indicate the bond angle(s) for each of the following molecules and ions. Also state whether the neutral molecules are polar or nonpolar.

(a) AsCl₅

(b) IF₃

(d) RnF₂

(e) SeCl₄

(f) SF₅^-

(g) XeF₄

Click for Solution

11-3)

(a)

Lewis structure:

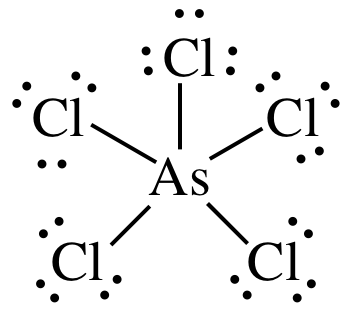
AB₅= trigonal bipyramidal, 3-D sketch:

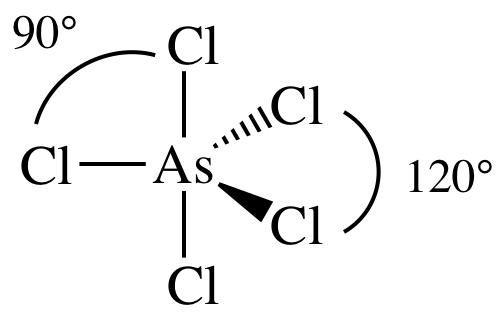
nonpolar molecule

(b)

Lewis structure:

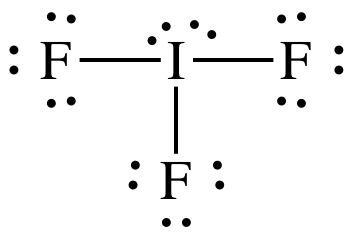
AB₃E₂ = T-shaped, 3-D sketch:

polar molecule

(c)

Lewis structure:

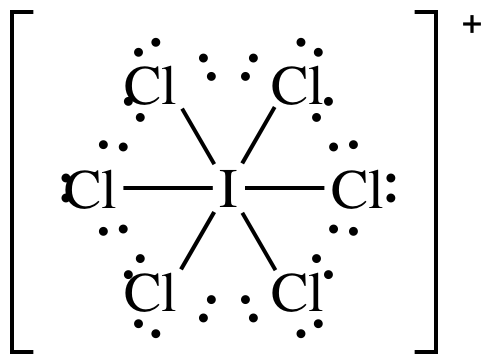
AB₆ = octahedral, 3-D sketch:

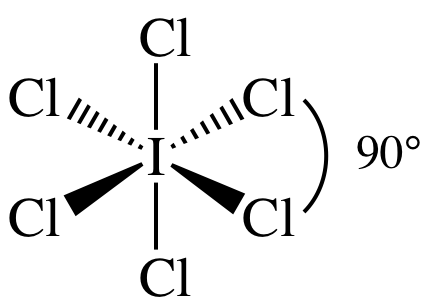
(d)

Lewis structure:

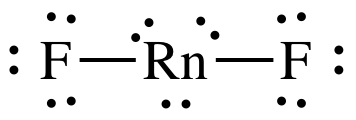
AB₂E₃ = linear, 3-D sketch:

nonpolar molecule

(e)

Lewis structure:

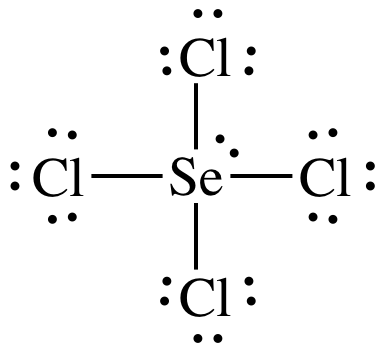
AB₄E₁ = seesaw, 3-D sketch:

polar molecule

(f)

Lewis structure:

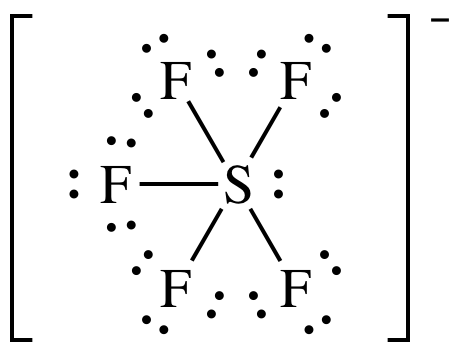
AB₅E₁ = square pyramidal, 3-D sketch:

(g)

Lewis structure:

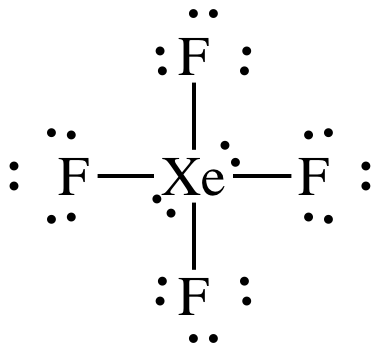
AB₄E₂ = square planar, 3-D sketch:

nonpolar molecule

11-4) Draw the Lewis structure and indicate the center atom hybridization for each of the following molecules and ions:

(a) H₂CO

(b) PH₂^-

Click for Solution

11-4)

(a)

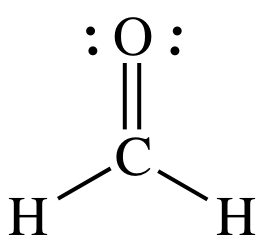
AB₃ = sp²

(b)

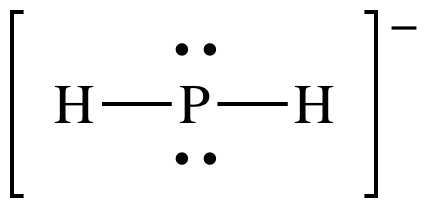
AB₂E₂ = sp³

(c)

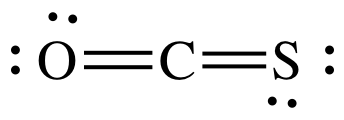
AB₂ = sp

11-5) Draw the Lewis structure for CH₃CN that has no formal charges and determine the number of sigma and pi bonds in the molecule.

Click for Solution

11-5)

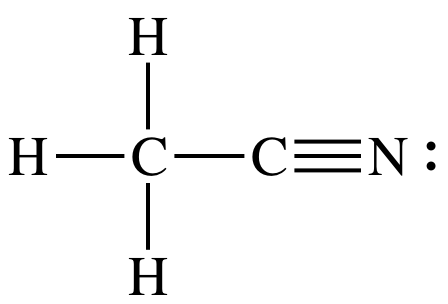
4 single + 1 triple = 4 sigma + 1(1 sigma + 2 pi) = 5 sigma bonds + 2 pi bonds

11-6)

(a) Write the molecular orbital diagram for B₂ and determine the bond order. Also state whether B₂ is diamagnetic or paramagnetic.

(b) Is the bond length of B₂⁺ shorter or longer than the bond length of B₂? Explain.

Click for Solution

11-6) (a) A B₂ molecule has 3 + 3 = 6 valence electrons:

↑↓	↑↓	↑	↑
σ_2s	σ_2s*	π_2p	π_2p	σ_2p	π_2p*	π_2p*	σ_2p*

bond order = 0.5(4-2) = 1

has unpaired electrons = paramagnetic

(b) B₂⁺ has one less bonding π_2p electron than B₂, which gives B₂⁺ a bond order of 0.5(3-2) = 0.5. Since B₂⁺ has a lower bond order than B₂, B₂⁺has a longer bond length than B₂.

Click for Review Quiz 1

Click for Review Quiz 1 Answers