Chapter 17: Acids and Bases
Section 17-1: Arrhenius Theory, pH, and pOH
Section 17-2: Monoprotic Strong Acids and Strong Bases
Section 17-3: Monoprotic Weak Acids
Section 17-4: Polyprotic Weak Acids and Sulfuric Acid
Section 17-7: Lewis Structures and Acid Strength
Section 17-8: Hydrolysis - Aqueous Ions as Acids and Bases
Section 17-9: Reactions of Nonmetal Oxides with Water to Create Oxoacids
Section 17-11: pH of Buffer Solutions
Section 17-12: pH and Titration Curves
Section 17-13: Acid-Base Indicators
Chapter 17 Practice Exercises and Review Quizzes
Section 17-1: Arrhenius Theory, pH, and pOH
Equation
1: pH = - log [H+]
Equation
2: pOH = - log [OH-]
[Note: When rounding the result y in a calculation y = - log x, the
number of decimal places in y should equal the number of significant figures in
x.]
In any aqueous solution, the
equilibrium reaction known as the autoionization of
water occurs:
H2O
(l) ⇌ H+
(aq) + OH- (aq)
Equation
3: Kw = [H+][OH-]
At 25°C, Kw
= 1.0 x 10-14.
Therefore, we can derive an equation relating pH and pOH
at 25°C as follows:
- log (Kw) = -log ([H+][OH-])
- log (1.0 x 10-14) = (- log [H+]) +
(-log [OH-])
Equation
4: 14.00 = pH + pOH
On the pH scale at 25°C:
pH < 7 = acidic
pH 7 = neutral
pH > 7 = basic
In this chapter, unless otherwise
indicated, assume all solutions are aqueous and at 25°C.
Section 17-2: Monoprotic
Strong Acids and Strong Bases
|
R |
HNO3 (aq) → H+
(aq) + NO3- (aq)
|
||
|
I |
Mi |
0 |
0 |
|
C |
-Mi |
+Mi |
+Mi |
|
E |
0 |
Mi |
Mi |
Once we know the molarity of H+ at equilibrium, we can also calculate the molarity of hydroxide ion (which, even in an acidic solution, is produced due to the autoionization of water), pH, and pOH as follows:
Sample Exercise 17A:
A 44 mL sample of HCl gas, measured at 45°C and 711 torr, was dissolved in water to yield 18.5 mL of solution. Calculate the molarity of hydrogen
ion, the molarity of hydroxide ion, pH, and pOH in this solution.
Solution:
First, use the Ideal Gas Law to
calculate the moles of HCl dissolved, then divide by the volume of solution to determine the
initial molarity of HCl:

Since HCl
is a strong acid, we now complete a RICE chart showing complete ionization
similar to that for HNO3 above:
|
R |
HCl (aq) → H+ (aq) + Cl- (aq)
|
||
|
I |
0.085 |
0 |
0 |
|
C |
-0.085 |
+0.085 |
+0.085 |
|
E |
0 |
0.085 |
0.085 |
We can now complete the calculations
using the equations above:
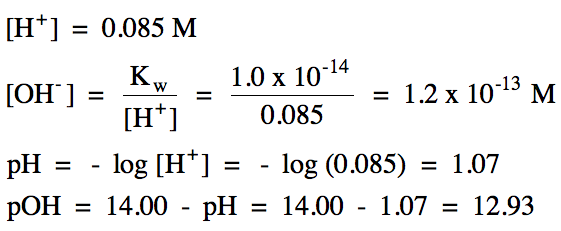
(Note that
we could have also calculated pOH using Equation 2.)
Soluble metal hydroxides are strong
bases that will ionize completely in water. If there is only one hydroxide ion per formula unit, the
initial molarity of the metal hydroxide will become
the molarity of hydroxide ion present in the solution
at equilibrium, as demonstrated below on the RICE chart for a sodium hydroxide
solution:
|
R |
NaOH (aq) → Na+
(aq) + OH- (aq)
|
||
|
I |
Mi |
0 |
0 |
|
C |
-Mi |
+Mi |
+Mi |
|
E |
0 |
Mi |
Mi |
However, if there are two hydroxide
ions per formula unit, the molarity of hydroxide ion
present in the solution at equilibrium will be twice the initial molarity of the metal hydroxide:
Sample Exercise 17B:
Solution:
First, convert the mass of calcium
hydroxide to moles, then divide by the volume of
solution to determine the initial molarity of calcium
hydroxide:
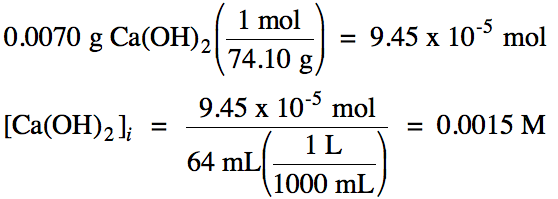
Since calcium hydroxide is a strong
base, we now complete a RICE chart showing complete ionization similar to that
for NaOH above:
|
R |
Ca(OH)2 (aq) → Ca2+
(aq) + 2 OH- (aq)
|
||
|
I |
0.0015 |
0 |
0 |
|
C |
-0.0015 |
+0.0015 |
+2(0.0015) |
|
E |
0 |
0.0015 |
0.0030 |

Section 17-3: Monoprotic
Weak Acids
For the remainder of this chapter,
assume that any acid that is not included on the strong acid list of HCl, HBr, HI, HNO3, or
HClO4 is a weak acid, meaning that only a fraction of the acid
molecules ionize in water. For the
ionization of a monoprotic weak acid, the RICE chart
and pH calculation will differ from that of a monoprotic
strong acid in the following ways:
1. A double equilibrium arrow will
be used in the ionization equation to indicate that the reverse reaction is
significant.
2. The initial molarity
of the weak acid will not decrease to zero as the reaction proceeds. As such, the molarity
of H+ present at equilibrium will be less than the initial molarity of the weak acid.
3. To determine the magnitude of
the change (C) line on the RICE chart, we will need to do an equilibrium
calculation. This will require
knowing the value of Kc for the ionization
reaction, which is typically expressed as Ka, known as the acid
ionization constant.
The RICE chart and equilibrium
calculation for all monoprotic weak acids will follow
the format below:
|
R |
HA (aq) ⇌ H+
(aq) + A- (aq)
|
||
|
I |
Mi |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
Mi - x |
x |
x |
(Note that
the anion A- may contain more hydrogen atoms, but we can assume that
these are not ionizable.)
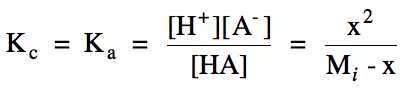
Once we know the value of x, we can
also calculate the percentage of the original sample of acid molecules that
have been ionized as follows:
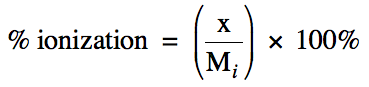
When comparing different monoprotic weak acids with the same initial molarity:
larger Ka = larger x = larger % ionization =
larger [H+] = lower pH = more acidic = stronger acid
Sample Exercise 17C:
Solution:
We complete the RICE chart and
equilibrium calculation for a monoprotic weak acid,
then use the value of x = [H+] to calculate the pH and percent
ionization:
|
R |
HF (aq) ⇌ H+
(aq) + F- (aq)
|
||
|
I |
0.16 |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
0.16 - x |
x |
x |

If we know the pH of a solution, we
can calculate [H+] as follows:
Equation 1a:
[H+] = 10-pH
If we know the initial molarity and the pH of a monoprotic
weak acid solution, we can calculate Ka as follows:
Sample
Exercise 17D:
Solution:
|
R |
HC2H3O2 (aq) ⇌ H+ (aq) + C2H3O2-
(aq)
|
||
|
I |
0.58 |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
0.58 - x |
x |
x |
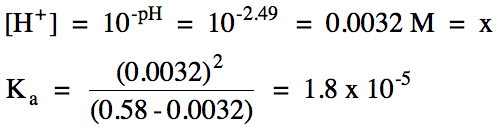
If we know the initial molarity and the percent ionization for a monoprotic weak acid, we can calculate pH and Ka,
as demonstrated at the end of the chapter in Practice Exercise 17-5. If we know the pH and Ka for
a monoprotic weak acid solution, we can calculate the
initial molarity, as demonstrated in Practice
Exercise 17-6.
Relative strengths of weak acids
can also be compared using pKa values:
pKa = -log Ka
Ka = 10-pKa
lower pKa = larger Ka = stronger acid
Section 17-4: Polyprotic
Weak Acids and Sulfuric Acid
A diprotic
weak acid will ionize in two steps as follows:
1st
ionization: H2A (aq) ⇌ H+
(aq) + HA- (aq) Kc = Ka1
2nd
ionization: HA- (aq) ⇌ H+
(aq) + A2- (aq) Kc = Ka2
A triprotic
weak acid will ionize in three steps as follows:
1st
ionization: H3A (aq) ⇌ H+
(aq) + H2A- (aq) Kc
= Ka1
2nd
ionization: H2A-
(aq) ⇌ H+
(aq) + HA2- (aq) Kc = Ka2
3rd
ionization: HA2- (aq) ⇌ H+
(aq) + A3- (aq) Kc = Ka3
The Ka values will
decrease with each successive ionization:
Ka1 > Ka2 > Ka3. In general, only the 1st
ionization will produce enough H+ to affect the pH, so we will only
use the RICE chart and equilibrium calculation from the 1st
ionization to calculate the pH:
Sample Exercise 17E:
Write the stepwise acid ionization
equations and calculate the pH of 1.6 M phosphoric acid, H3PO4,
which has the following acid ionization constants:
Ka1
= 7.5 x 10-3
Ka2
= 6.2 x 10-8
Ka3
= 4.2 x 10-13
Solution:
We obtain the pH by completing the
RICE chart and equilibrium calculation for the 1st ionization only,
after which we proceed with writing the 2nd and 3rd
ionization equations:
|
R |
H3PO4 (aq) ⇌ H+
(aq) + H2PO4-
(aq)
|
||
|
I |
1.6 |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
1.6 - x |
x |
x |
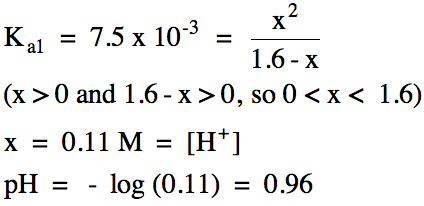
2nd
ionization: H2PO4-
(aq) ⇌ H+
(aq) + HPO42- (aq)
3rd
ionization: HPO42-
(aq) ⇌ H+
(aq) + PO43- (aq)
Sulfuric acid is a unique case
where the 1st ionization of H2SO4 occurs
completely with a negligible reverse reaction (similar to a monoprotic
strong acid), whereas only a fraction of the HSO4- anions
further ionize in the 2nd ionization (similar to a diprotic weak acid):
1st
ionization: H2SO4
(aq) → H+
(aq) + HSO4- (aq)
2nd
ionization: HSO4-
(aq) ⇌ H+
(aq) + SO42- (aq)
Section 17-5: Bronsted
Theory
Bronsted acid = proton (H+) donor
Bronsted base = proton (H+) acceptor
In the case of an ammonia solution,
water will act as a Bronsted acid to donate a proton
to the Bronsted base ammonia. Since the Bronsted
acid water loses a proton, the formula will decrease by one
hydrogen and the charge will decrease by 1, thus producing the hydroxide
ion that makes the solution basic.
At the same time, the Bronsted base ammonia
will gain a proton, so the formula will increase by one
hydrogen and the charge will increase by 1 to produce the ammonium ion:
NH3
(aq) + H2O (l) ⇌ NH4+
(aq) + OH- (aq)
Although we have used Arrhenius
theory to write acid ionization equations and will continue to do so, we could
have chosen to use Bronsted theory instead. In the case of solution containing the monoprotic weak acid HA, water can act as a Bronsted base to accept a proton from the Bronsted acid HA:
HA (aq) + H2O (l) ⇌ H3O+
(aq) + A- (aq)
The cation
H3O+ is known as the hydronium
ion and can replace H+ when calculating pH after writing the acid
ionization equation according to Bronsted
theory: pH = - log [H3O+]. Since liquid water will be omitted from
the RICE chart and Ka expression, the pH calculated using Bronsted theory will be the same
as the pH calculated using Arrhenius theory.
As shown above, water acts as a Bronsted acid in an ammonia solution, but a Bronsted base in an acid solution. A molecule or ion that can act as both
a Bronsted acid or a Bronsted
base in different situations is said to be amphoteric
(or amphiprotic).
Bronsted theory
also applies to proton transfer reactions in which water is not a reactant or a
product:
Sample Exercise 17F:
Identify the Bronsted
acids and bases in the forward and reverse directions for the reaction below:
CO32-
(aq) + HC2O4- (aq) ⇌ HCO3-
(aq) + C2O42- (aq)
Solution:
forward reaction:
Bronsted acid = HC2O4-
(donates proton), Bronsted base = CO32-
(accepts proton)
reverse reaction:
Bronsted acid = HCO3-, Bronsted base = C2O42-
After a proton
has been donated by a Bronsted acid, the
resulting molecule or ion is known as the conjugate base. After a proton has
been accepted by a Bronsted base, the
resulting molecule or ion is known as the conjugate acid:
Sample Exercise 17G:
Write the formula for:
a. the
conjugate acid of HS-
b. the
conjugate base of HC4H4O6-
Solution:
a. conjugate
acid = add H+ to formula = H2S
b. conjugate
base = remove H+ from formula = C4H4O62-
Section 17-6: Weak Bases
For a solution of a neutral weak
base B, the base ionization equation can be represented:
B (aq) + H2O (l) ⇌ BH+ (aq) + OH- (aq)
(proton is typically added at end of base formula)
Kc for the
reaction above can be expressed as Kb, known as the base ionization
constant. To calculate
the pH and percent ionization in a weak base solution, we complete a RICE chart
and equilibrium calculation similar to that for a monoprotic
weak acid. However, the column
under liquid water will be omitted from the RICE chart and water will be
omitted from the Kb expression. Also note that the calculated value of x = [OH-],
not the molarity of hydrogen ions:
|
R |
B (aq) + H2O(l) ⇌ BH+
(aq) + OH- (aq)
|
|||
|
I |
Mi |
|
0 |
0 |
|
C |
-x |
+x |
+x |
|
|
E |
Mi - x |
x |
x |
|
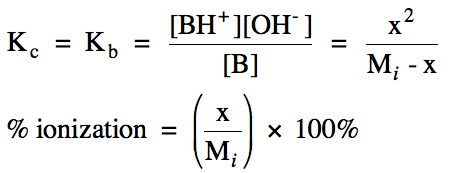
When comparing different weak bases
with the same initial molarity:
larger Kb = larger x = larger % ionization =
larger [OH-] = higher pH = more basic = stronger base
Sample Exercise 17H:
Calculate the pH and percent
ionization of 0.029 M ammonia (Kb = 1.8 x 10-5).
Solution:
|
R |
NH3 (aq)
+ H2O(l)
⇌ NH4+
(aq) + OH- (aq)
|
|||
|
I |
0.029 |
|
0 |
0 |
|
C |
-x |
+x |
+x |
|
|
E |
0.029- x |
x |
x |
|
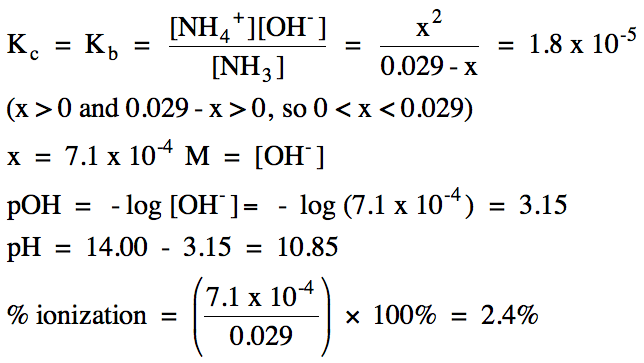
If we know the pOH
of a solution, we can calculate [OH-] as follows:
Equation 2a:
[OH-] = 10-pOH
If we know the initial molarity and the pH of a weak base solution, we can calculate Kb as follows:
Sample Exercise 17I:
A 0.026 M methylamine solution has
a pH of 11.51. Write the base
ionization equation and calculate Kb for methylamine, CH3NH2.
Solution:
|
R |
CH3NH2 (aq) +
H2O(l) ⇌ CH3NH3+
(aq)
+
OH- (aq)
|
|||
|
I |
0.026 |
|
0 |
0 |
|
C |
-x |
+x |
+x |
|
|
E |
0.026- x |
x |
x |
|
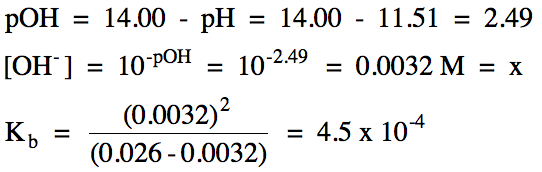
If we know the initial molarity and the percent ionization for a weak base, we can
calculate pH and Kb, as demonstrated in Practice Exercise
17-12. If we know the pH and Kb
for a weak base solution, we can calculate the initial molarity,
as demonstrated in Practice Exercise 17-13.
Relative strengths of weak bases
can also be compared using pKb values:
pKb = -log Kb
Kb = 10-pKb
lower pKb = larger Kb = stronger base
The Lewis structure for an oxoacid (or oxyacid) with the
formula HmXOn will generally
show the center atom X bonded to each oxygen atom, and each hydrogen atom will
be bonded to a different oxygen atom, as demonstrated below for sulfurous acid,
H2SO3:
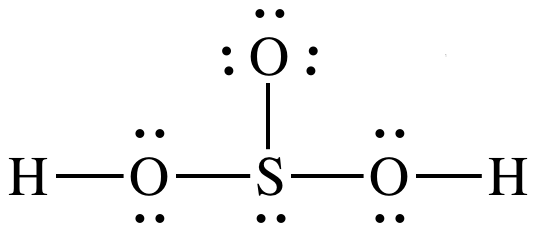
(other resonance structures also acceptable)
To compare the relative strengths
of oxoacids, use the following guidelines:
1. More terminal oxygens (= oxygens not bonded to
a hydrogen = n-m) = oxoacid donates proton more
readily = stronger acid.
2. Higher electronegativity
of center atom X = oxoacid donates proton more
readily = stronger acid.
Sample Exercise 17J:
Draw Lewis structures for nitric
acid, HNO3, and phosphoric acid, H3PO4. Which is the stronger acid? Give two reasons to justify your
answer.
Solution:
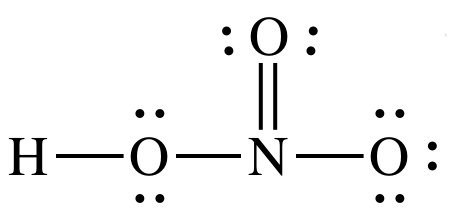
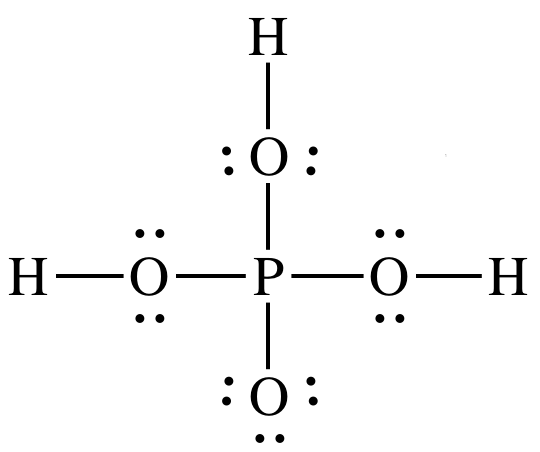
Nitric acid
is stronger acid because:
1. HNO3
has more terminal oxygens (3-1=2) than H3PO4
(4-3=1).
2. Electronegativity for central atom N is higher than for
central atom P.
The Lewis structure for a monoprotic organic acid with the formula RCOOH, where R can
either represent a single atom or a group of atoms, is shown below:
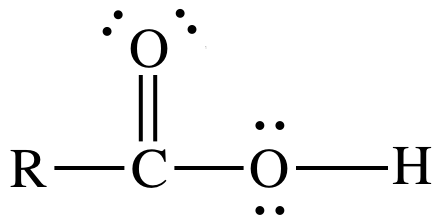
The ionizable
proton will be the one single-bonded to the oxygen atom on the right end of the
Lewis structure, not in R. To
compare the relative strengths of organic acids, use the following general
guidelines:
1. Higher electronegativity
of atoms in R = organic acid donates proton more readily = stronger acid.
2. Highly electronegative atoms in
R are closer in proximity to ionizable hydrogen =
organic acid donates proton more readily = stronger acid.
Sample Exercise 17K:
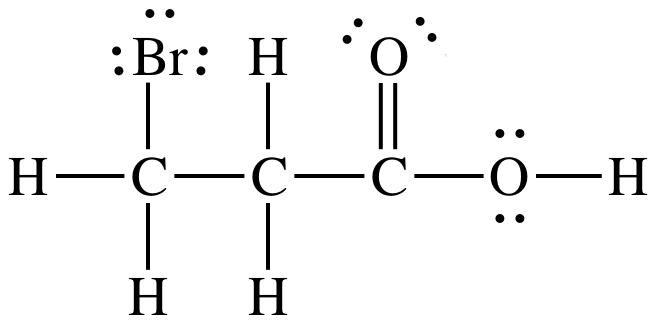
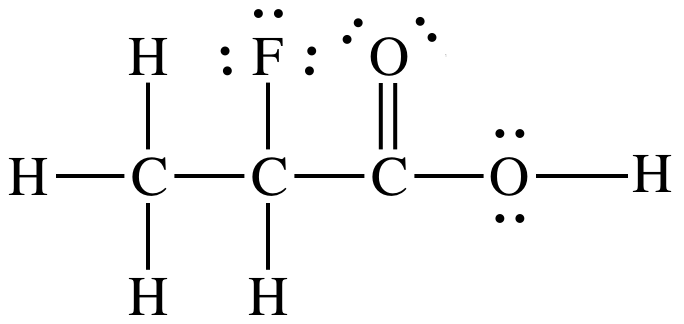
Solution:
1. Electronegativity of F is higher than Br.
2. F is
closer to ionizable proton than Br.
Section 17-8: Hydrolysis – Aqueous Ions as
Acids and Bases
1. A cation
BH+ containing an ionizable proton
(ammonium, NH4+, for example) will generally hydrolyze as
a weak acid:
BH+
(aq) ⇌ H+
(aq) + B (aq)
We can determine Ka for
the reaction above by utilizing the fact that when two reactions are added to
obtain a third reaction, the product of the equilibrium constants for the two
added reactions will equal the equilibrium constant for the third reaction:
BH+
(aq) ⇌ H+
(aq) + B (aq) Ka
for BH+ = ???
B (aq) + H2O (l) ⇌ BH+
(aq) + OH- (aq) Kb
for B = given in problem or found on Kb data table
__________________________________________________________________________________________
H2O
(l) ⇌ H+
(aq) + OH- (aq) Kw = 1.0 x 10-14
(Ka
for BH+)(Kb for B) = Kw
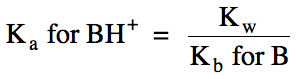
(so stronger base B = weaker conjugate acid BH+)
2. Metal cations
will generally not hydrolyze and, therefore, will be spectator ions that do not
affect the pH. Notable exceptions include Al3+ and Fe3+.
3. An anion will generally
hydrolyze as a weak base:
A-
(aq) + H2O (l) ⇌ HA (aq) + OH- (aq)
We can determine Kb for
the reaction above as follows:
A-
(aq) + H2O (l) ⇌ HA (aq) + OH- (aq) Kb
for A- = ???
HA (aq) ⇌ H+
(aq) + A- (aq) Ka
for HA = given in problem or found on Ka data table
_________________________________________________________________________________
H2O
(l) ⇌ H+
(aq) + OH- (aq) Kw = 1.0 x 10-14
(Kb
for A-)(Ka for HA) = Kw
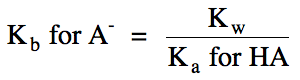
(so stronger acid HA = weaker conjugate base A-)
4. Anions found in monoprotic strong acids (Cl-,
Br-, I-, NO3-, ClO4-)
do not hydrolyze as weak bases to any significant extent, so these five anions
will be spectator ions that do not affect the pH.
Using the guidelines above, we can
predict if an ionic compound solution will be acidic, basic, or neutral as
follows:
A. If both the cation
and the anion are spectator ions, the solution will be neutral.
B. If only the cation
hydrolyzes and the anion is a spectator ion, the solution will be acidic.
C. If the cation
is a spectator ion and only the anion hydrolyzes, the solution will be basic.
D. If both the cation
and anion hydrolyze, then we must compare the equilibrium constants for the two hydrolysis reactions:
if Ka for BH+ > Kb for A-,
then solution is acidic
if Ka for BH+ < Kb for A-,
then solution is basic
if Ka for BH+ = Kb for A-,
then solution is neutral
Sample Exercise 17L:
|
Acid |
Ka |
|
HC2H3O2 |
1.8 x 10-5 |
|
HNO2 |
4.5 x 10-4 |
|
Base |
Kb |
|
C5H5N |
1.7 x 10-9 |
|
CH3NH2 |
4.4 x 10-4 |
a. Mg(NO3)2
b. CH3NH3Cl
[composed of CH3NH3+ and Cl-]
c. NaC2H3O2
d. C5H5NHNO2
[composed of C5H5NH+ and NO2-]
Solution:
b. Cl-
= spectator ion, CH3NH3+ hydrolyzes as weak
acid = solution is acidic:
CH3NH3+
(aq) ⇌ H+
(aq) + CH3NH2 (aq)
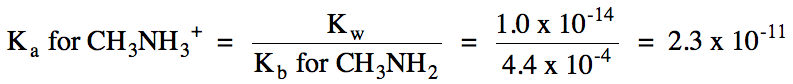
c. Na+ = spectator ion,
C2H3O2- hydrolyzes as a weak base =
solution is basic:
C2H3O2-
(aq) + H2O (l) ⇌ HC2H3O2
(aq) + OH- (aq)
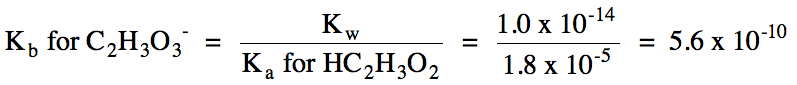
d. Both ions hydrolyze, so we must
compare equilibrium constants:
C5H5NH+
(aq) ⇌ H+
(aq) + C5H5N (aq)
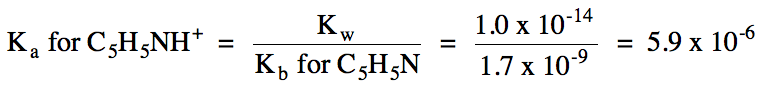
NO2-
(aq) + H2O (l) ⇌ HNO2
(aq) + OH- (aq)
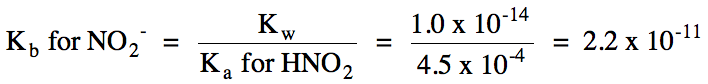
Ka
> Kb = solution is acidic
To calculate the pH of a solution
where only the cation hydrolyzes as a weak acid and
the anion is a spectator ion, we complete a RICE chart and equilibrium
calculation similar to that completed earlier for a neutral monoprotic
weak acid. To calculate the pH of
a solution where only the anion hydrolyzes as a weak base and the cation is a spectator ion, we complete a RICE chart and
equilibrium calculation similar to that completed earlier for a neutral weak
base.
Sample Exercise 17M:
For each solution below, show any
relevant hydrolysis reactions and calculate the pH.
a. 1.6 M NH4I (Kb
for NH3 = 1.8 x 10-5)
b. 0.84 M KClO
(Ka for HClO = 3.0 x 10-8)
Solution:
|
R |
NH4+ (aq) ⇌ H+
(aq) + NH3
(aq)
|
||
|
I |
1.6 |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
1.6 - x |
x |
x |
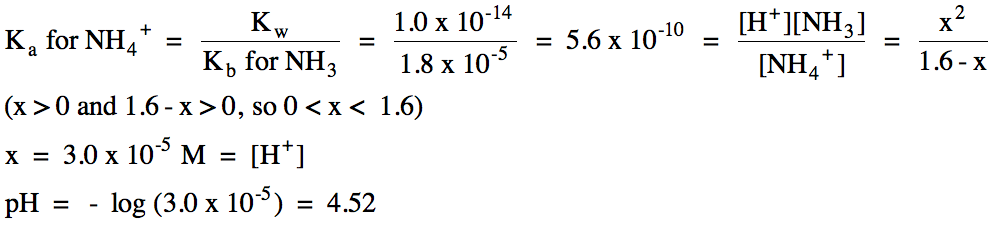
b. K+ = spectator ion, ClO- hydrolyzes as a weak base:
|
R |
ClO-
(aq) + H2O(l)
⇌ HClO (aq) +
OH- (aq)
|
|||
|
I |
0.84 |
|
0 |
0 |
|
C |
-x |
+x |
+x |
|
|
E |
0.84- x |
x |
x |
|
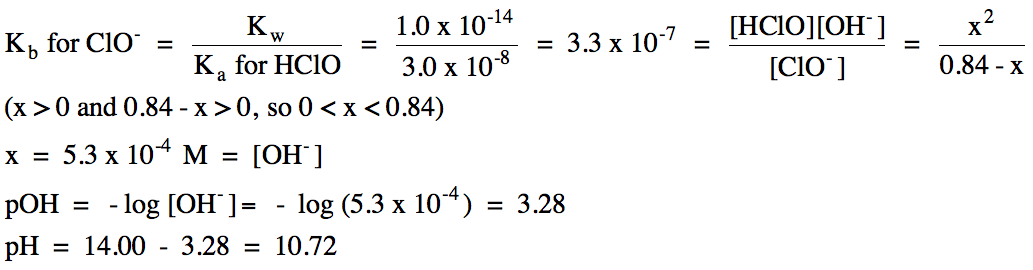
If a solution contains metal
cations that are spectator ions along with anions of the type HA-, a
portion of the HA- ions will ionize as weak acids while the
remainder of the HA- ions will hydrolyze as weak bases:
weak acid
ionization reaction:
HA- (aq) ⇌ H+ (aq) + A2- (aq) Ka for HA- = Ka2 for H2A
weak base
hydrolysis reaction:
HA- (aq) + H2O (l) ⇌ H2A
(aq) + OH- (aq) Kb for HA- = Kw/(Ka1 for H2A)
For anions of the type H2A-,
the relevant reactions that affect the pH are:
weak acid
ionization reaction:
H2A- (aq) ⇌ H+ (aq) + HA2- (aq) Ka for H2A- = Ka2 for H3A
weak base
hydrolysis reaction:
H2A- (aq) + H2O (l) ⇌ H3A
(aq) + OH- (aq) Kb for H2A- = Kw/(Ka1 for H3A)
For anions of the type HA2-,
the relevant reactions that affect the pH are:
weak acid
ionization reaction:
HA2- (aq) ⇌ H+ (aq) + A3- (aq) Ka for HA2- = Ka3 for H3A
weak base
hydrolysis reaction:
HA2- (aq) + H2O (l) ⇌ H2A- (aq) + OH- (aq) Kb for HA2- = Kw/(Ka for H2A- = Ka2 for H3A)
To determine if an HA-,
H2A-, or HA2- solution is acidic or basic, we
must compare the equilibrium constants for the weak acid ionization reaction
and the weak base hydrolysis reaction:
if Ka > Kb, then solution is acidic
if Ka < Kb, then solution is basic
Sample Exercise 17N:
Predict whether a solution of
sodium bicarbonate, NaHCO3, will be acidic or basic. Show all relevant reactions that affect
the pH and also give the value of the equilibrium constant for each reaction
you write. For carbonic acid, H2CO3,
Ka1 = 4.3 x 10-7 and Ka2 = 5.6 x 10-11
Solution:
Na+ = spectator ion
weak acid
ionization reaction:
HCO3- (aq) ⇌ H+ (aq) + CO32- (aq)
Ka for HCO3- = Ka2 for H2CO3 = 5.6 x 10-11
weak base
hydrolysis reaction:
HCO3- (aq) + H2O (l) ⇌ H2CO3 (aq) + OH- (aq)
Kb for HCO3- = 1.0 x 10-14/(Ka1 for H2CO3 = 4.3
x 10-7) = 2.3 x 10-8
Ka < Kb = solution is basic
nonmetal oxide + water → oxoacid with no change in
oxidation numbers
For example, the reaction of SO2
(oxidation number of S = +4) and water will produce H2SO3
(oxidation number of S = +4) rather than H2SO4 (oxidation
number of S = +6).
Sample Exercise 17O:
Will the reaction of N2O5
and water produce HNO2 or HNO3? Write a balanced equation for the reaction.
Solution:
The reaction of N2O5
(oxidation number of N = +5) and water will produce HNO3 (oxidation
number of N = +5) rather than HNO2 (oxidation number of N =
+3). The balanced equation will be
N2O5 + H2O → 2 HNO3.
Section 17-10: Experiment – Determining the
Molar Mass of an Unknown Monoprotic Weak Acid by
Titration
1. Dissolve a known mass of HA in
water.
2. Titrate the HA solution with a
metal hydroxide solution of known molarity from a buret. Record
the volume of metal hydroxide solution required to reach
the equivalence point.
3. Use stoichiometry from the net
ionic equation HA (aq) + OH- (aq) → H2O
(l) + A- (aq) to calculate the moles of HA
reacted, then divide the mass of HA by moles of HA to obtain the molar mass of
HA.
Sample Exercise 17P:
b. In a separate experiment, 6.7
grams of the acid was dissolved in 25 mL of water and
then titrated with 0.85 M barium hydroxide. The volume of base required to reach the equivalence point
was 45 mL.
Calculate the molar mass and determine the molecular formula of the
acid.
Solution:
a. 100% - 54.53% C - 9.15% H = 36.32%O by mass.
Assume one
hundred grams of unknown acid:
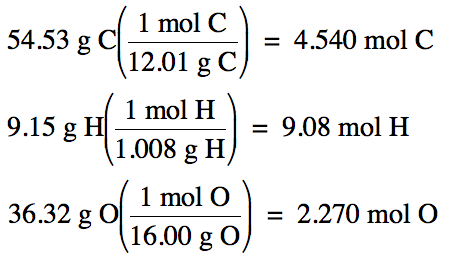
4.540 mol
C: 9.08 mol H: 2.270 mol O (divide each by 2.270)
= 2 mol C:
4 mol H: 1 mol O
Therefore,
empirical formula is C2H4O.
b. 0.85 M Ba(OH)2 → 0.85 M Ba2+ and 2 x
0.85 M = 1.7 M OH-
Use stoichiometry
from the net ionic equation HA (aq) + OH-
(aq) → H2O
(l) + A- (aq) to calculate the moles of HA
reacted, then divide the mass of HA by moles of HA to obtain the molar mass of
HA. Note that the volume of water
used to dissolve the HA is not relevant in this calculation:
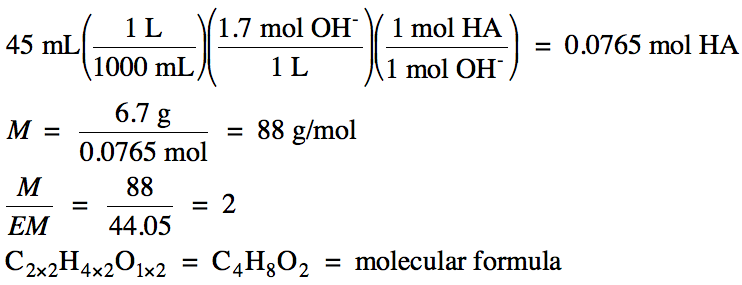
Since the acid is monoprotic, we can rewrite the molecular formula as HC4H7O2.
Section 17-11: pH of Buffer Solutions
One type of buffer solution
contains significant concentrations of both a weak acid HA and its conjugate
base A-. When HA and A- are mixed in solution, the presence of a significant concentration of A- reduces the ionization of HA in the reaction HA (aq) ⇌ H+ (aq) + A- (aq). This is
an example of the common-ion effect. We will generally assume that the common-ion effect reduces ionization
of HA to an extent where the initial concentrations and moles of HA and A- in the solution upon mixing are effectively equal to their equilibrium
concentrations and moles. Therefore, for the ionization of HA in an HA/A- buffer
solution, we can use initial rather than equilibrium concentrations and moles
in the Ka expression below:
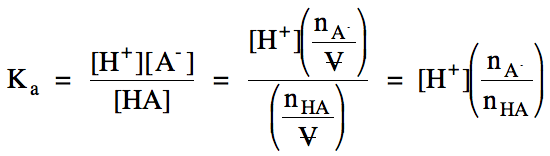
A variation of the expression above
known as the Henderson-Hasselbalch equation can be used to calculate the pH of
an HA/A- buffer solution directly and can derived as follows:
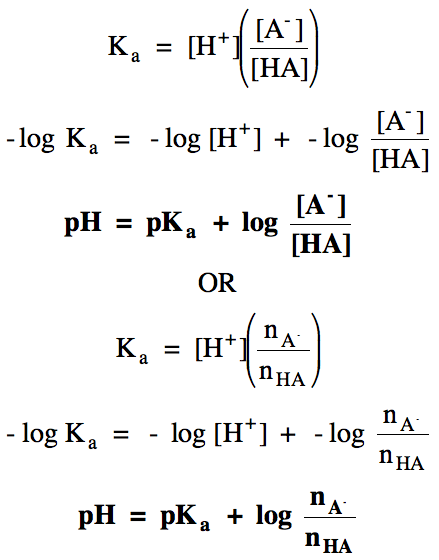
Sample Exercise 17Q:
Calculate the pH of a solution
containing 0.46 grams of NaF in 75 mL of 0.20 M HF (Ka = 6.8 x 10-4).
Solution:
Na+ = spectator ion, HF/F- = buffer solution:
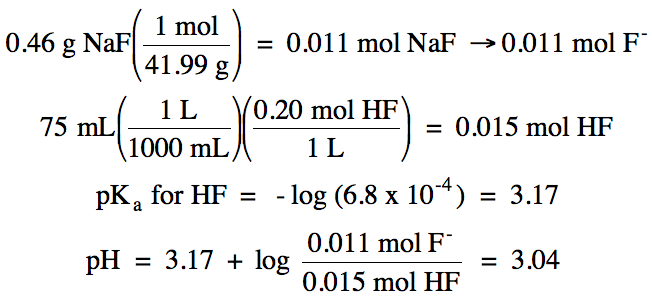
An HA/A- buffer solution
is able to maintain a constant pH as water is added because the ratios [A-]/[HA]
and nA-/nHA will not change upon dilution. However, the solution will eventually
cease functioning as an effective buffer if the volume is increased to a point
where the concentrations of HA and A- are too low.
A second type of buffer solution
contains significant concentrations of both a weak base B and its conjugate
acid BH+. When B and BH+ are mixed in solution, the presence of a significant concentration of BH+ reduces the ionization of B in the reaction B (aq) + H2O (l) ⇌ BH+ (aq) + OH- (aq). This
is another example of the common-ion effect. We will generally assume that the common-ion effect reduces
ionization of B to an extent where the initial concentrations and moles of B
and BH+ in the solution upon mixing are effectively equal to their
equilibrium concentrations and moles. Therefore, for the ionization of B in a B/BH+ buffer solution,
we can use initial rather than equilibrium concentrations and moles in the Kb expression below:
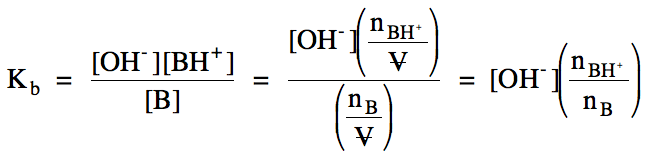
A variation of the expression above
can be used to calculate the pH of a B/BH+ buffer solution directly
and can derived as follows:
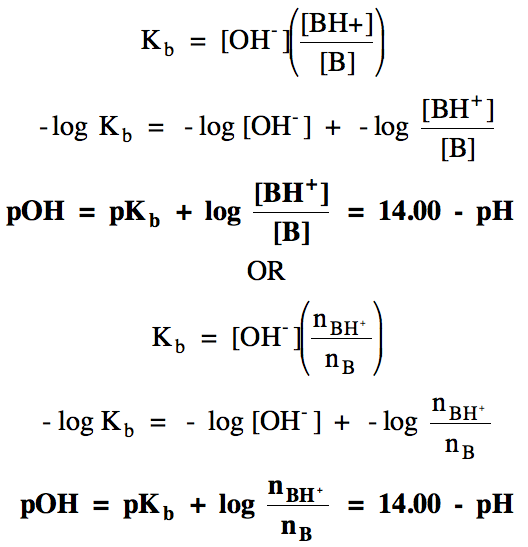
Sample Exercise 17R:
Calculate the pH of a solution
containing 3.0 grams of NH4Cl in 30. mL of 1.6 M NH3 (Kb = 1.8 x 10-5).
Solution:
Cl- = spectator ion, NH3/NH4+ = buffer solution:
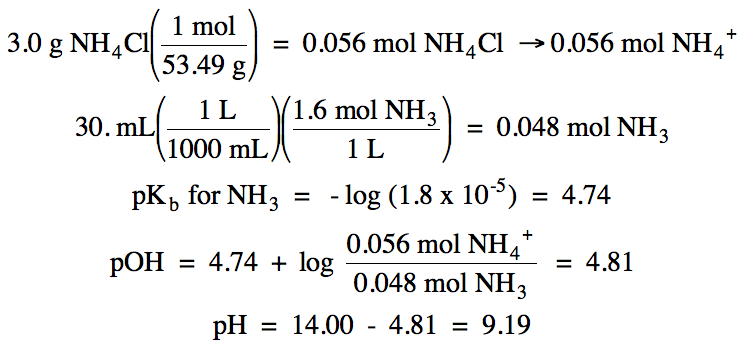
A B/BH+ buffer solution
is able to maintain a constant pH as water is added because the ratios [BH+]/[B]
and nBH+/nB will not change upon dilution. However, the solution will eventually
cease functioning as an effective buffer if the volume is increased to a point
where the concentrations of B and BH+ are too low.
Even if the amount of strong acid
or strong base added to pure water is small, the pH can still change from pH =
7 by several units. For example,
if 0.001 mol H+ is added to water to create 1 L of 0.001 M H+,
the new pH = -log (0.001) = 3.0. Likewise, if 0.001 mol OH- is added to water to create 1 L of
0.001 M OH-, the new pOH = -log (0.001) = 3.0 and the new pH = 11.0.
On the other hand, the pH will only
change slightly as small increments of strong acid or strong base are added to
an HA/A- or B/BH+ buffer solution. The H+ or OH- added will be neutralized by buffer components and the new pH of the buffer
solution calculated as follows (based on 1:1 stoichiometric mole ratios and assuming the H+ or OH- added is the limiting reagent):
OH- added to HA/A- buffer:
neutralization
reaction: HA (aq) + OH- (aq) → A- (aq) + H2O (l)
pH = pKa + log (nA- + nOH-)/(nHA - nOH-)
(only valid
if nHA > nOH-)
H+ added to HA/A- buffer:
neutralization
reaction: A- (aq) + H+ (aq) → HA (aq)
pH = pKa + log (nA- - nH+)/(nHA + nH+)
(only valid
if nA- > nH+)
H+ added to B/BH+ buffer:
neutralization
reaction: B (aq) + H+ (aq) → BH+ (aq)
pOH = pKb + log (nBH+ + nH+) /(nB - nH+) =
14.00 - pH
(only valid
if nB > nH+)
OH- added to B/BH+ buffer:
neutralization
reaction: BH+ (aq) + OH- (aq) → B (aq) + H2O
(l)
pOH = pKb + log (nBH+ - nOH-)/(nB + nOH-) =
14.00 - pH
(only valid
if nBH+ > nOH-)
Sample Exercise 17S:
Write the net ionic equation for
the neutralization reaction that occurs and calculate the pH when:
a. 0.001 mol HCl is added to the
solution in Sample Exercise 17Q
b. 0.001 mol NaOH is added to the
solution in Sample Exercise 17Q
c. 0.001 mol HCl is added to the
solution in Sample Exercise 17R
d. 0.001 mol NaOH is added to the
solution in Sample Exercise 17R
Solution:
a. Cl- = spectator ion
neutralization
reaction: F- (aq) + H+ (aq) → HF (aq)
pH = 3.17 +
log (0.011 – 0.001) mol F-/(0.015 + 0.001) mol HF = 2.97
b. Na+ = spectator ion
neutralization
reaction: HF (aq) + OH- (aq) → F- (aq) + H2O (l)
pH = 3.17 +
log (0.011 + 0.001) mol F-/(0.015 - 0.001) mol HF = 3.10
c. Cl- = spectator ion
neutralization
reaction: NH3 (aq) + H+ (aq) → NH4+ (aq)
pOH = 4.74
+ log (0.056 + 0.001) mol NH4+/(0.048 - 0.001) mol NH3 = 4.82
pH = 14.00
– 4.82 = 9.18
d. Na+ = spectator ion
neutralization
reaction: NH4+ (aq) + OH- (aq) → NH3 (aq) + H2O (l)
pOH = 4.74
+ log (0.056 - 0.001) mol NH4+/(0.048 + 0.001) mol NH3 = 4.79
pH = 14.00
– 4.79 = 9.21
Rather than mixing HA and A- or B and BH+ to create a buffer solution, we can also create an HA/A- or B/BH+ buffer solution via a neutralization reaction if the H+ or OH- added is the limiting reagent and the other reactant is in
excess. If that is not the case,
then the method of calculating the pH of the resulting solution after the neutralization
reaction is complete is also described below:
OH- added to HA:
neutralization
reaction: HA (aq) + OH- (aq) → A- (aq) + H2O (l)
nHA > nOH-: HA/A- buffer created, pH = pKa + log (nA- produced/nHA excess)
nHA = nOH-: A- solution created, pOH = 14.00 - pH calculated using RICE chart for hydrolysis
of weak base A-
nHA < nOH-: OH-/A- solution created, pOH = 14.00 – pH = -log [OH-]excess (hydrolysis of A- negligible)
H+ added to A-:
neutralization
reaction: A- (aq) + H+ (aq) → HA (aq)
nA- > nH+: HA/A- buffer created, pH = pKa + log (nA- excess/nHA produced)
nA-
= nH+: HA solution
created, pH calculated using RICE chart for ionization of weak acid HA
nA- < nH+: H+/HA
solution created, pH = -log [H+]excess (ionization of HA
negligible)
H+ added to B:
neutralization
reaction: B (aq) + H+ (aq) → BH+ (aq)
nB > nH+: B/BH+ buffer created, pOH = pKb + log (nBH+ produced/nB excess) = 14.00 - pH
nB = nH+: BH+ solution created, pH calculated using RICE chart for hydrolysis of weak acid BH+
nB < nH+: H+/BH+ solution created, pH = -log [H+]excess (hydrolysis of BH+ negligible)
OH- added to BH+:
neutralization
reaction: BH+ (aq) + OH- (aq) → B (aq) + H2O
(l)
nBH+> nOH-: B/BH+ buffer created, pOH = pKb + log (nBH+ excess/nB produced) = 14.00 - pH
nBH+
= nOH-: B solution
created, pOH = 14.00 - pH calculated using RICE chart for ionization of weak
base B
nBH+< nOH-: OH-/B
solution created, pOH = 14.00 – pH = -log [OH-]excess (ionization of B negligible)
Sample
Exercise 17T:
Write the net ionic equation for
the neutralization reaction that occurs in each aqueous mixture below. Which one of the four reactions creates
a buffer solution? For each
mixture, describe the method of calculating the pH of the resulting solution
after the neutralization reaction is complete.
a. 0.1 mol HBr + 0.1 mol CH3NH2 (a weak base)
b. 0.3 mol HI + 0.1 mol KC3H5O3
c. 0.3 mol NH4NO3 + 0.1 mol NaOH
d. 0.1 mol HNO2 and 0.1
mol KOH
Solution:
a. Br- = spectator ion
neutralization
reaction: CH3NH2 (aq) + H+ (aq) → CH3NH3+ (aq)
n of CH3NH2 = nH+: CH3NH3+ solution created, pH calculated using RICE chart for hydrolysis of weak acid CH3NH3+
b. I- and K+ = spectator ions
neutralization
reaction: C3H5O3- (aq) + H+ (aq) → HC3H5O3 (aq)
n of C3H5O3- < nH+: H+/
HC3H5O3 solution created, pH = -log [H+]excess (ionization of HC3H5O3 negligible)
c. NO3- and
Na+ = spectator ions
neutralization
reaction: NH4+ (aq) + OH- (aq) → NH3 (aq) + H2O (l)
n of
NH4+ > nOH-: NH3/ NH4+ buffer created, pOH = pKb + log (n of NH4+ excess/n of NH3 produced) = 14.00 - pH
d. K+ = spectator ion
neutralization
reaction: HNO2 (aq) +
OH- (aq) → NO2- (aq) + H2O (l)
n of HNO2 = nOH-: NO2- solution created, pOH = 14.00 - pH calculated using RICE chart for hydrolysis
of weak base NO2-
Section
17-12: pH and Titration Curves
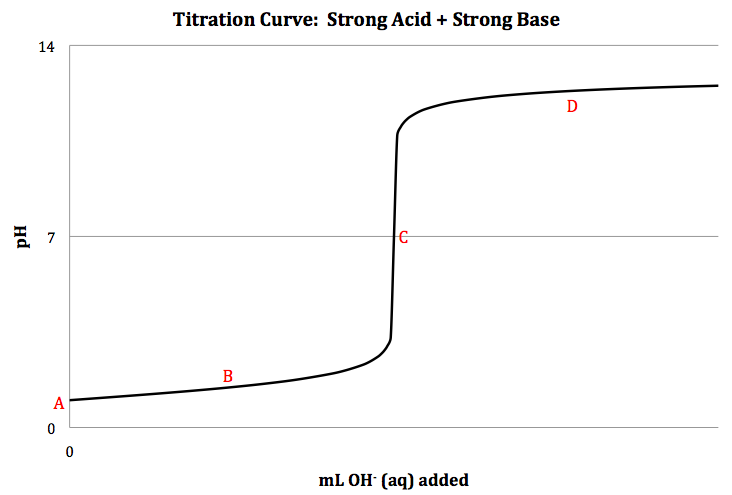
A titration curve is a graph
showing the pH at different points during a titration:
Strong Acid + Strong Base Titration
When a strong acid is titrated with
a strong base, the net ionic equation for the neutralization reaction is H+ (aq) + OH- (aq) → H2O
(l), and a sketch of the titration curve is shown below:
Stoichiometry can
be used to calculate the volume of base needed to reach the equivalence point
as follows:
LH+ × MH+ = nH+ = nOH-/ MOH- = LOH-
We can calculate
the pH at different points on the titration curve above as follows:
Point A = initial:
pH = -log [H+]
Point B = between start of titration and equivalence point:
pH = -log [H+]excess = -log [(nH+ - nOH-)/L
total]
Point C = equivalence point:
nH+ = nOH- = only H2O (l) present so pH =
7
Point D = after equivalence point:
pOH = -log [OH-]excess = -log [(nOH- - nH+)/L
total] = 14.00 - pH
Sample Exercise 17U:
a. Write the net ionic equation for
the neutralization reaction that occurs during the titration of 24 mL of 0.30 M
HCl with 0.20 M NaOH and calculate the volume of base needed to reach the
equivalence point.
b. Calculate the following:
i. the initial pH
ii. the pH after 22 mL of base has
been added
iii. the pH at the equivalence
point
iv. the pH after 48 mL of base has
been added
Solution:
a. Cl- and Na+ = spectator ions, neutralization reaction: H+ (aq) + OH- (aq) → H2O (l)
0.024 L (0.30 mol H+/1
L) = 0.0072 mol H+ = 0.0072 mol OH- (1 L/0.20 mol OH-)
= 0.036 L = 36 mL base needed
b.
i. pH = -log (0.30) = 0.52
ii. 0.022 L (0.20 mol OH-/1
L) = 0.0044 mol OH- added
pH = -log [(0.0072 - 0.0044) mol H+ excess/(0.024 + 0.022) L total] = 1.22
iii. only H2O present,
pH = 7
iv. 0.048 L (0.20 mol OH-/1
L) = 0.0096 mol OH- added
pOH = - log [(0.0096 - 0.0072) mol
OH- excess/(0.024 + 0.048) L total] = 1.48
pH = 14.00 – 1.48 = 12.52
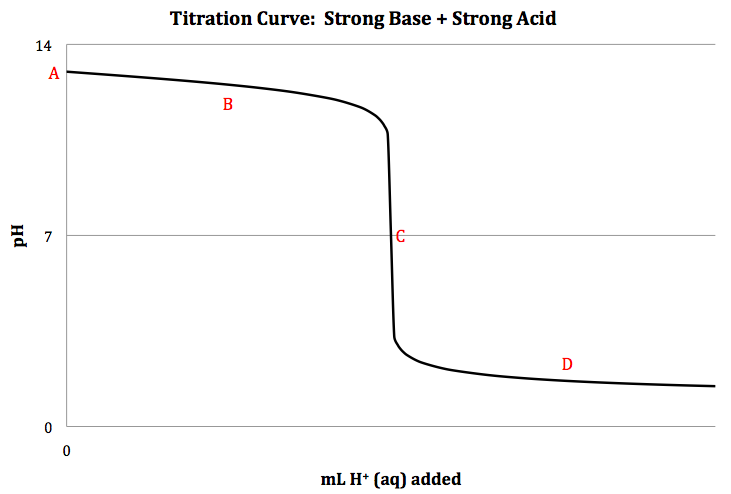
Strong Base + Strong Acid Titration
When a strong base is titrated with
a strong acid, the net ionic equation for the neutralization reaction is OH- (aq) + H+ (aq) → H2O
(l), and a sketch of the titration curve is shown below:
Stoichiometry can
be used to calculate the volume of acid needed to reach the equivalence point
as follows:
LOH- × MOH- = nOH- = nH+/ MH+ = LH+
We can calculate
the pH at different points on the titration curve above as follows:
Point A = initial:
pOH = -log [OH-] = 14.00 - pH
Point B = between start of titration and equivalence point:
pOH = -log [OH-]excess = -log [(nOH- - nH+)/L
total] = 14.00 - pH
Point C = equivalence point:
nOH- = nH+ = only H2O (l) present so pH =
7
Point D = after equivalence point:
pH = -log [H+]excess = -log [(nH+ - nOH-)/L
total]
We will
demonstrate how to calculate the pH at different points in the titration of a
strong base with a strong acid below in Practice Exercise 17-29.
Weak Acid + Strong Base Titration
When a weak acid is titrated with a
strong base, the net ionic equation for the neutralization reaction is HA (aq)
+ OH- (aq) → H2O
(l) + A- (aq), and a sketch of the titration curve is shown below:
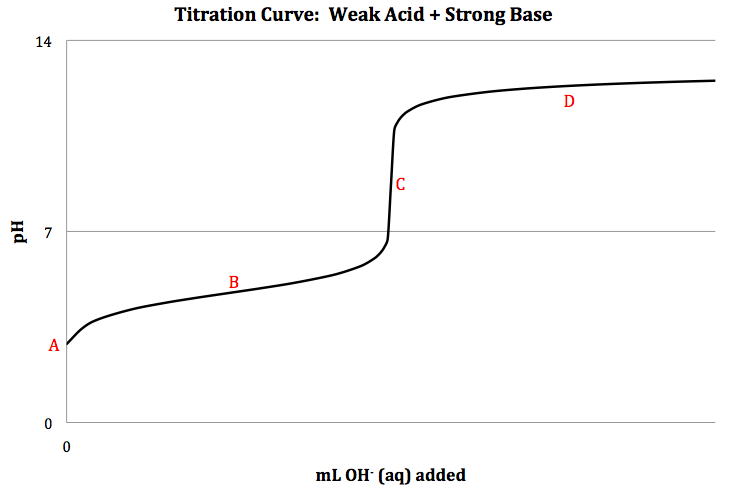
Stoichiometry can
be used to calculate the volume of base needed to reach the equivalence point
as follows:
LHA × MHA = nHA = nOH-/ MOH- = LOH-
We can calculate
the pH at different points on the titration curve above as follows:
Point A = initial pH calculated using RICE chart for ionization of weak
acid HA:
R
|
HA (aq) ⇌ H+ (aq) + A- (aq)
|
||
I
|
Mi
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
E
|
Mi - x
|
x
|
x
|
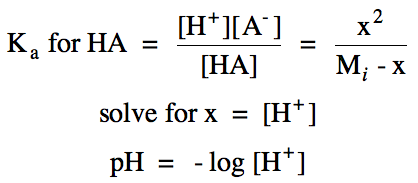
Point B = between start of titration and equivalence point = HA/A- buffer solution created:
nOH- added = nHA reacted = nA- produced
nHA initial - nHA reacted = nHA excess
pH = pKa + log (nA- produced/nHA excess)
halfway to equivalence point: nA- produced = nHA excess, so pH = pKa
Point C = equivalence point, pOH = 14.00 - pH calculated using
RICE chart for hydrolysis of weak base A-:
R
|
A- (aq) + H2O(l) ⇌ HA
(aq) + OH- (aq)
|
|||
I
|
Mi
|
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
|
E
|
Mi - x
|
x
|
x
|
|
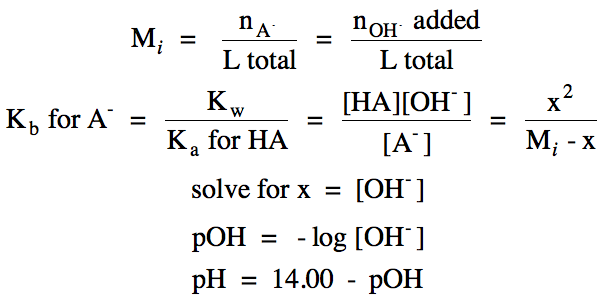
pH > 7 at equivalence point
Point D = after equivalence point (hydrolysis of A- negligible):
pOH = -log [OH-]excess = -log [(nOH- - nHA)/L
total] = 14.00 - pH
Sample Exercise 17V:
a. Write the net ionic equation for
the neutralization reaction that occurs during the titration of 16 mL of 0.20 M
HC2H3O2 (Ka = 1.8 x 10-5)
with 0.10 M KOH and calculate the volume of base needed to reach the
equivalence point.
b. Calculate the following:
i. the initial pH
ii. the pH after 14 mL of base has
been added
iii. the pH at the equivalence
point
iv. the pH after 44 mL of base has
been added
Solution:
a. K+ = spectator ion,
neutralization reaction: HC2H3O2 (aq) + OH- (aq) → H2O
(l) + C2H3O2- (aq)
0.016 L (0.20 mol HC2H3O2/1
L) = 0.0032 mol HC2H3O2 = 0.0032 mol OH- (1 L/0.10 mol OH-) = 0.032 L = 32 mL base needed
b.
i.
R
|
HC2H3O2 (aq) ⇌ H+ (aq) + C2H3O2- (aq)
|
||
I
|
0.20
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
E
|
0.20 - x
|
x
|
x
|
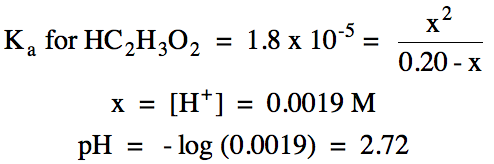
ii.
0.014 L (0.10 mol OH-/1 L) = 0.0014 mol OH- added =
0.0014 mol HC2H3O2 reacted = 0.0014 mol C2H3O2- produced
0.0032 mol
HC2H3O2 initial
- 0.0014 mol HC2H3O2 reacted = 0.0018 mol HC2H3O2 excess
pKa for HC2H3O2 = -log (1.8 x 10-5) = 4.74
pH = 4.74 + log (0.0014 mol C2H3O2-/0.0018 mol HC2H3O2) =
4.63
iii.
R
|
C2H3O2- (aq) + H2O(l) ⇌ HC2H3O2 (aq) + OH- (aq)
|
|||
I
|
Mi
|
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
|
E
|
Mi - x
|
x
|
x
|
|
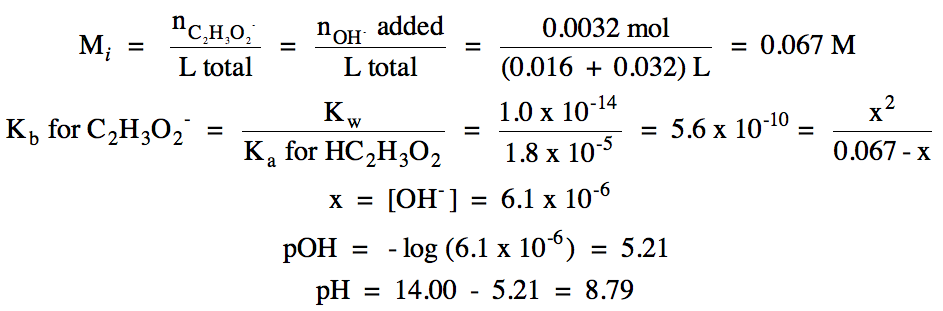
iv. 0.044 L (0.10 mol OH-/1
L) = 0.0044 mol OH- added
pOH = - log [(0.0044 - 0.0032) mol
OH- excess/(0.016 + 0.044) L total] = 1.70
pH = 14.00 – 1.70 = 12.30
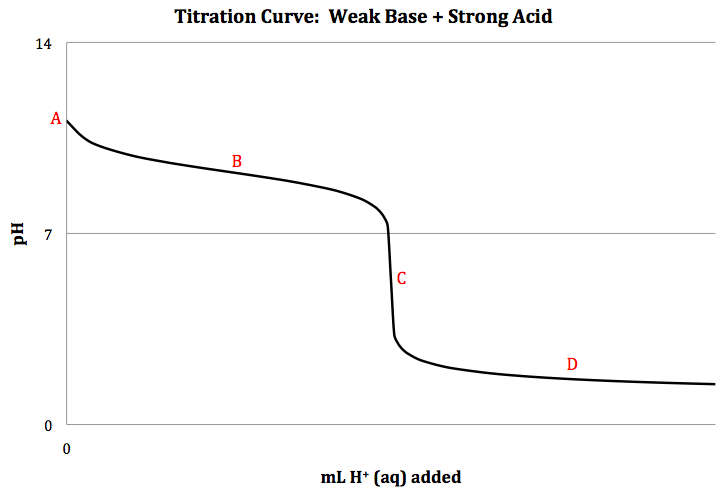
Weak Base + Strong Acid Titration
When a weak base is titrated with a
strong acid, the net ionic equation for the neutralization reaction is B (aq) +
H+ (aq) → BH+ (aq), and a sketch of the titration curve is shown below:
Stoichiometry can
be used to calculate the volume of acid needed to reach the equivalence point
as follows:
LB × MB = nB = nH+/ MH+ = LH+
We can calculate
the pH at different points on the titration curve above as follows:
Point A = initial pH calculated using RICE chart for ionization of weak
base B:
R
|
B (aq) + H2O(l) ⇌ BH+ (aq) + OH- (aq)
|
|||
I
|
Mi
|
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
|
E
|
Mi - x
|
x
|
x
|
|
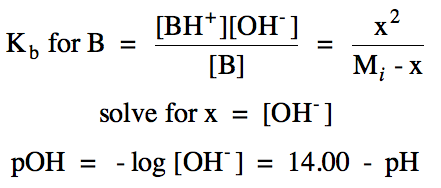
Point B = between start of titration and equivalence point = B/BH+ buffer solution created:
nH+ added = nB reacted = nBH+ produced
nB initial - nB reacted = nB excess
pOH = pKb + log (nBH+ produced/nB excess) = 14.00 - pH
halfway to equivalence point: nBH+ produced = nB excess, so pOH = pKb = 14.00 - pH
Point C = equivalence point, pH calculated using RICE chart for
hydrolysis of weak acid BH+:
R
|
BH+ (aq) ⇌ H+ (aq) + B (aq)
|
||
I
|
Mi
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
E
|
Mi - x
|
x
|
x
|
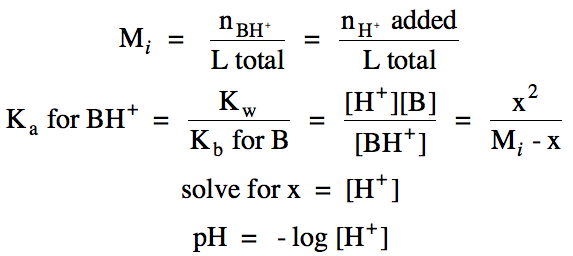
pH < 7 at equivalence point
Point D = after equivalence point (hydrolysis of BH+ negligible):
pH = -log [H+]excess = -log [(nH+ - nB)/L
total]
Sample Exercise 17W:
a. Write the net ionic equation for
the neutralization reaction that occurs during the titration of 54 mL of 0.10 M
NH3 (Kb = 1.8 x 10-5) with 0.30 M HCl and
calculate the volume of acid needed to reach the equivalence point.
b. Calculate the following:
i. the initial pH
ii. the pH after 11 mL of acid has
been added
iii. the pH at the equivalence
point
iv. the pH after 32 mL of acid has
been added
Solution:
a. Cl- = spectator ion,
neutralization reaction: NH3 (aq) + H+ (aq) → NH4+ (aq)
0.054 L (0.10 mol NH3/1
L) = 0.0054 mol NH3 = 0.0054 mol H+ (1 L/0.30 mol H+)
= 0.018 L = 18 mL acid needed
b.
i.
R
|
NH3 (aq) + H2O(l) ⇌ NH4+ (aq) + OH- (aq)
|
|||
I
|
0.10
|
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
|
E
|
0.10 - x
|
x
|
x
|
|
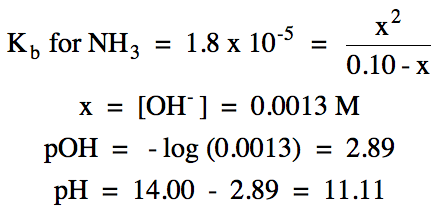
ii.
0.011 L (0.30 mol H+/1 L) = 0.0033 mol H+ added =
0.0033 mol NH3 reacted = 0.0033 mol NH4+ produced
0.0054 mol NH3 initial
- 0.0033 mol NH3 reacted = 0.0021 mol NH3 excess
pKb for NH3 = -log (1.8 x 10-5) = 4.74
pOH = 4.74 + log (0.0033 mol NH4+/0.0021 mol NH3) = 4.94
pH = 14.00 – 4.94 = 9.06
iii.
R
|
NH4+ (aq) ⇌ H+ (aq) + NH3 (aq)
|
||
I
|
Mi
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
E
|
Mi - x
|
x
|
x
|
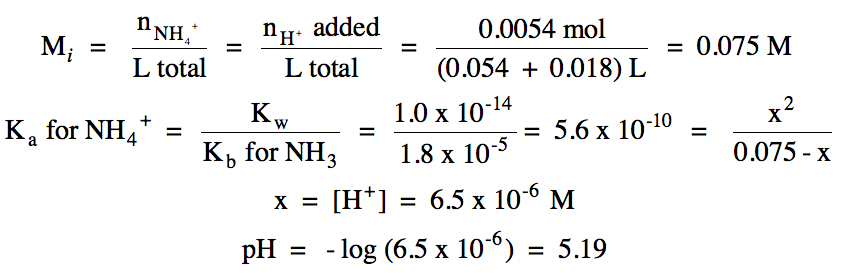
iv. 0.032 L (0.30 mol H+/1
L) = 0.0096 mol H+ added
pH = - log [(0.0096 - 0.0054) mol H+ excess/(0.054 + 0.032) L total] = 1.31
Section 17-13: Acid-Base Indicators
One type of acid-base indicator is
a weak acid where the neutral acid HInd has a different color than its
conjugate base Ind-:
HInd (=
color 1) ⇌ H+ + Ind- (= color 2)
The pH of the solution being tested
will determine the ratio of moles of Ind- to moles of HInd and,
therefore, the color of the indicator as follows:
pH of
solution = pKa for HInd + log (nInd-/nHInd)
pH <<
pKa: nInd- << nHInd = color 1
pH = pKa: nInd- = nHInd =
mixture of color 1 and color 2
pH >>
pKa: nInd- >> nHInd = color 2
During each titration discussed
above, the pH changes sharply by several units near the equivalence point. An appropriate indicator for a
titration will have one color before the equivalence point and then
instantaneously change to a different color after the equivalence point due to
the sharp change in pH. The
indicator chosen should have pKa for HInd close to the pH at the
equivalence point:
titration: choose indicator with pKa for HInd close to pH at equivalence
point
Sample Exercise 17X:
Which indicator, thymolphthalein (Ka = 1 x 10-10) or bromcresol green (Ka = 8 x 10-6),
would be the better choice for the titration in Sample Exercise 17W?
Solution:
pH at
equivalence point = 5.19
pKa for thymolphthalein = -log (1 x 10-10) = 10.0
pKa for bromcresol green = -log (8 x 10-6) = 5.1
pKa for bromcresol green close to pH at equivalence point, so bromcresol green is better choice
Chapter 17 Practice Exercises and Review Quizzes:
17-1) A 74 mL
sample of HI gas, measured at 55°C and 694 mmHg, was dissolved in water to
yield 48 mL of solution. Calculate the molarity
of hydrogen ion, the molarity of hydroxide ion, pH,
and pOH in this solution.
Click for Solution
17-1)

HI = strong
acid:
|
R |
HI (aq) → H+
(aq) + I- (aq)
|
||
|
I |
0.052 |
0 |
0 |
|
C |
-0.052 |
+0.052 |
+0.052 |
|
E |
0 |
0.052 |
0.052 |
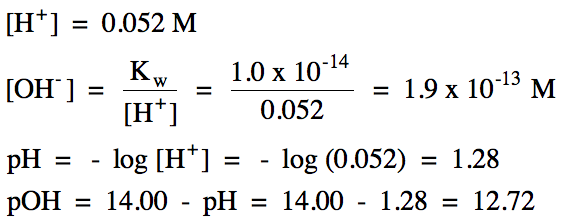
17-2) A
0.054 gram sample of barium hydroxide was dissolved in water to create 75 mL of solution.
Calculate the molarity of hydroxide ion, the molarity of hydrogen ion, pOH,
and pH in this solution.
Click for Solution
17-2)
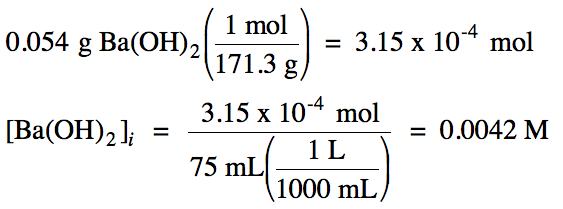
Ba(OH)2
= strong base:
|
R |
Ba(OH)2 (aq) → Ba2+
(aq) + 2 OH- (aq)
|
||
|
I |
0.0042 |
0 |
0 |
|
C |
-0.0042 |
+0.0042 |
+2(0.0042) |
|
E |
0 |
0.0042 |
0.0084 |
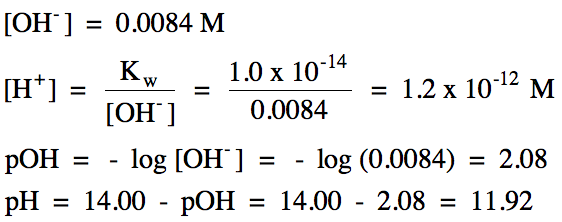
17-3) Write the acid ionization
equation and calculate the pH and percent ionization of 0.87 M hypochlorous acid, HClO (Ka
= 3.0 x 10-8).
Click for Solution
17-3)
|
R |
HClO (aq) ⇌ H+
(aq) + ClO-
(aq)
|
||
|
I |
0.87 |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
0.87 - x |
x |
x |
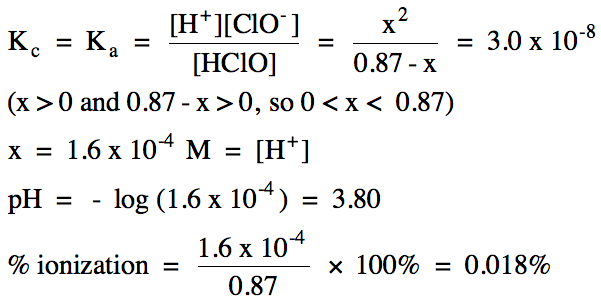
17-4) A 0.92 M hydrocyanic acid
solution has a pH of 4.68. Write
the acid ionization equation and calculate Ka for hydrocyanic acid,
HCN.
Click for Solution
17-4)
|
R |
HCN (aq) ⇌ H+
(aq) + CN- (aq)
|
||
|
I |
0.92 |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
0.92 - x |
x |
x |
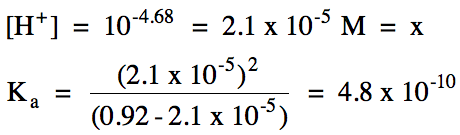
17-5) A 0.046 M solution of benzoic
acid is 3.6% ionized. Write the
acid ionization equation and calculate the pH of the solution and Ka
for benzoic acid, HC7H5O2.
Click for Solution
17-5)
|
R |
HC7H5O2 (aq) ⇌ H+ (aq) + C7H5O2-
(aq)
|
||
|
I |
0.046 |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
0.046 - x |
x |
x |
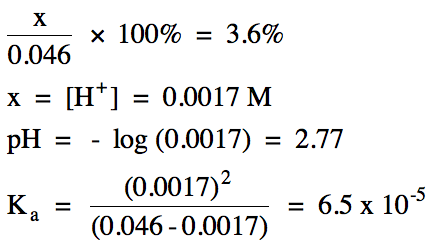
17-6) A nitrous acid, HNO2,
solution has a pH of 2.58. Given
that Ka = 4.5 x 10-4 for nitrous acid, write the acid
ionization equation and calculate the initial molarity
of the nitrous acid solution.
Click for Solution
17-6)
|
R |
HNO2 (aq) ⇌ H+
(aq) + NO2-
(aq)
|
||
|
I |
Mi |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
Mi - x |
x |
x |
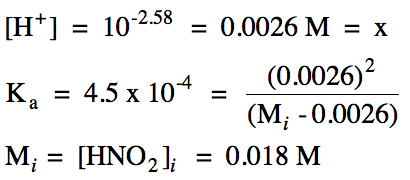
17-7) Write the stepwise acid
ionization equations and calculate the pH of 0.073 M sulfurous acid, H2SO3,
which has the following acid ionization constants:
Ka1
= 1.7 x 10-2
Ka2
= 6.4 x 10-8
Click for Solution
17-7)
|
R |
H2SO3 (aq) ⇌ H+
(aq) + HSO3-
(aq)
|
||
|
I |
0.073 |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
0.073 - x
|
x |
x |
2nd ionization: HSO3- (aq) ⇌ H+ (aq) + SO32- (aq)
17-8) Identify
the Bronsted acids and bases in the forward and
reverse directions for the reaction below:
HPO42-
(aq) + H2AsO4- (aq) ⇌ H2PO4-
(aq) + HAsO42- (aq)
Click for Solution
17-8)
forward reaction:
Bronsted acid = H2AsO4-
(donates proton), Bronsted base = HPO42-
(accepts proton)
reverse reaction:
Bronsted acid = H2PO4-,
Bronsted base = HAsO42-
17-9) Write
the formula for:
a. the
conjugate acid of HC6H5O72-
b. the
conjugate base of HC3H2O4-
Click for Solution
17-9)
a. conjugate
acid = add H+ to formula = H2C6H5O7-
b. conjugate
base = remove H+ from formula = C3H2O42-
17-10) Write the base ionization
equation and calculate the pH and percent ionization of 0.11 M pyridine, C5H5N
(Kb = 1.7 x 10-9).
Click for Solution
17-10)
|
R |
C5H5N (aq) + H2O(l) ⇌ C5H5NH+
(aq) + OH- (aq)
|
|||
|
I |
0.11 |
|
0 |
0 |
|
C |
-x |
+x |
+x |
|
|
E |
0.11- x |
x |
x |
|
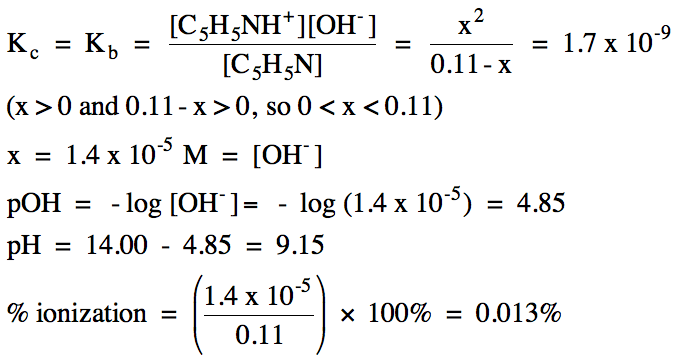
17-11) A 0.72 M aniline solution
has a pH of 9.26. Write the base
ionization equation and calculate Kb for aniline, C6H5NH2.
Click for Solution
17-11)
|
R |
C6H5NH2 (aq)
+ H2O(l) ⇌ C6H5NH3+
(aq) + OH- (aq)
|
|||
|
I |
0.72 |
|
0 |
0 |
|
C |
-x |
+x |
+x |
|
|
E |
0.72- x |
x |
x |
|
17-12) A 0.052 M solution of
ethylamine is 10.6% ionized. Write
the base ionization equation and calculate the pH of the solution and Kb
for ethylamine, C2H5NH2.
Click for Solution
17-12)
|
R |
C2H5NH2 (aq)
+ H2O(l) ⇌ C2H5NH3+
(aq) + OH- (aq)
|
|||
|
I |
0.052 |
|
0 |
0 |
|
C |
-x |
+x |
+x |
|
|
E |
0.052- x |
x |
x |
|
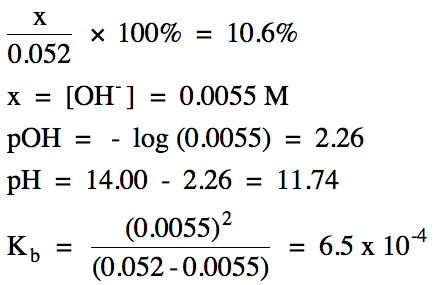
17-13) A trimethylamine,
(CH3)3N, solution has a pH of
11.68. Given that Kb =
6.4 x 10-5 for trimethylamine, write the
base ionization equation and calculate the initial molarity
of the trimethylamine solution.
Click for Solution
17-13)
|
R |
(CH3)3N
(aq) + H2O(l) ⇌ (CH3)3NH+
(aq) + OH- (aq)
|
|||
|
I |
Mi |
|
0 |
0 |
|
C |
-x |
+x |
+x |
|
|
E |
Mi - x |
x |
x |
|
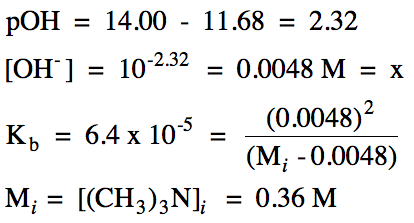
17-14) Draw Lewis structures for
arsenic acid, H3AsO4, and sulfuric acid, H2SO4. Which is the stronger acid? Give two reasons to justify your
answer.
Click for Solution
17-14)
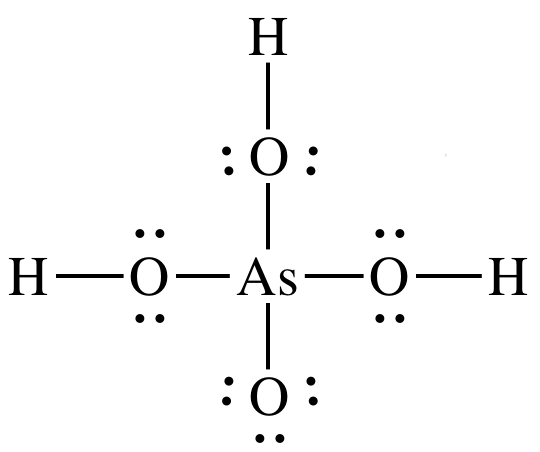
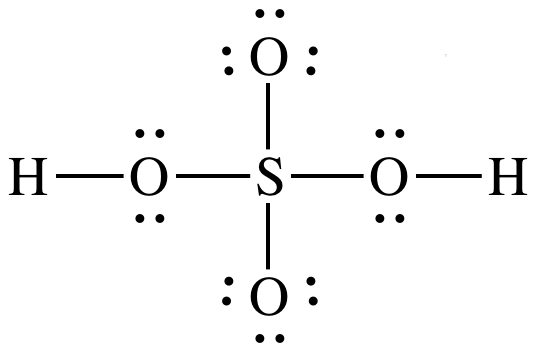
Sulfuric
acid is stronger acid because:
1. H2SO4
has more terminal oxygens (4-2=2) than H3AsO4
(4-3=1).
2. Electronegativity for central atom S is higher than for
central atom As.
17-15) Which
of the two acids shown below is the stronger acid? Give two reasons to justify your answer.
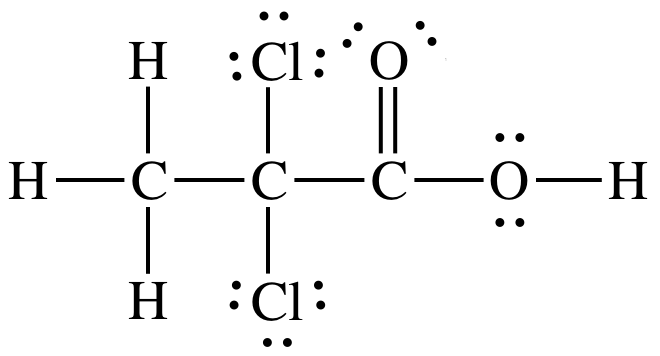
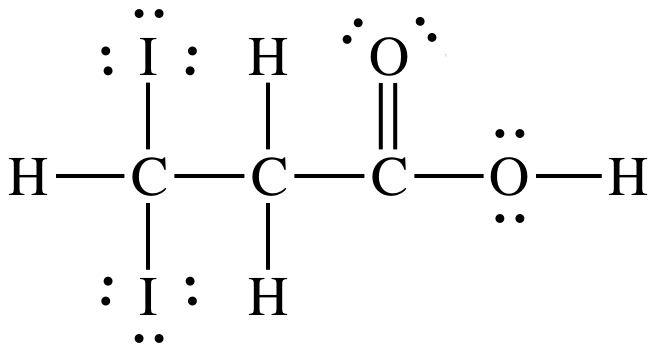
Click for Solution
17-15)
The top
acid is stronger because:
1. Electronegativity of Cl is higher
than I.
2. Cl atoms are closer to ionizable
proton than I atoms.
17-16) Predict whether a solution
of each compound below will be acidic, basic, or neutral. For solutions that are not neutral,
show all relevant hydrolysis reactions that affect the pH and also calculate
the equilibrium constant for each reaction you write using information from the
following data tables:
|
Acid |
Ka |
|
HClO |
3.0 x 10-8 |
|
HF |
6.8 x 10-4 |
|
Base |
Kb |
|
NH3 |
1.8 x 10-5 |
|
(CH3)3N |
6.4 x 10-5 |
a. KF
b. (CH3)3NHClO
[composed of (CH3)3NH+ and ClO-]
c. Ca(ClO4)2
d. NH4Br
Click for Solution
17-16)
a. K+ = spectator ion, F-
hydrolyzes as a weak base = solution is basic:
F-
(aq) + H2O (l) ⇌ HF (aq) + OH- (aq)
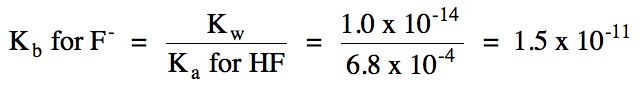
b. Both ions hydrolyze, so we must
compare equilibrium constants:
(CH3)3NH+ (aq) ⇌ H+
(aq) + (CH3)3N (aq)
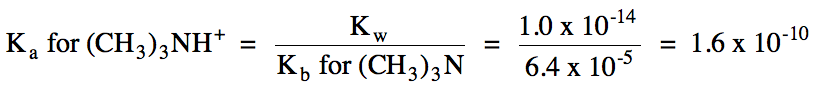
ClO- (aq) + H2O (l) ⇌ HClO
(aq) + OH- (aq)
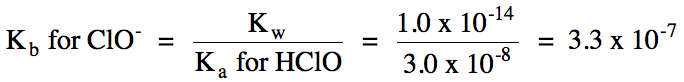
Ka
< Kb = solution is basic
c. Ca2+ and ClO4-
= spectator ions = solution is neutral
d. Br- = spectator ion,
NH4+ hydrolyzes as weak acid = solution is acidic:
NH4+
(aq) ⇌ H+
(aq) + NH3 (aq)
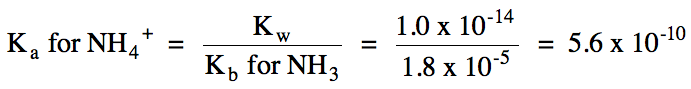
17-17) For
each solution below, show any relevant hydrolysis reactions and calculate the
pH.
a. 1.8 M NaNO2 (Ka
for HNO2 = 4.5 x 10-4)
b. 0.66 M CH3NH3NO3
[composed of CH3NH3+ and NO3-]
(Kb for CH3NH2 = 4.4 x 10-4)
Click for Solution
17-17)
a. Na+ = spectator ion,
NO2- hydrolyzes as a weak base:
|
R |
NO2- (aq)
+ H2O(l)
⇌ HNO2
(aq) + OH- (aq)
|
|||
|
I |
1.8 |
|
0 |
0 |
|
C |
-x |
+x |
+x |
|
|
E |
1.8- x |
x |
x |
|
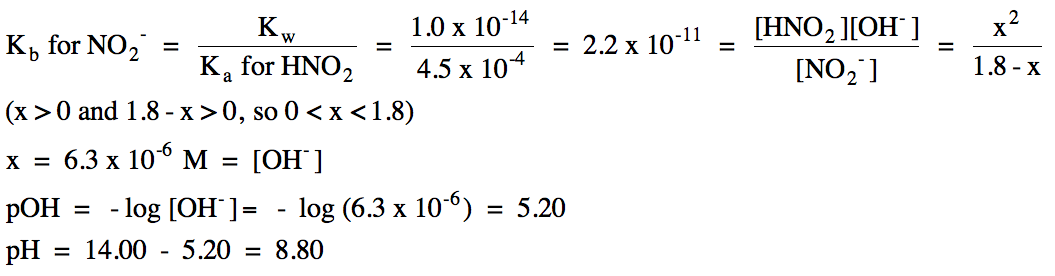
b. NO3- =
spectator ion, CH3NH3+ hydrolyzes as a weak
acid:
|
R |
CH3NH3+ (aq) ⇌ H+ (aq) + CH3NH2 (aq)
|
||
|
I |
0.66 |
0 |
0 |
|
C |
-x |
+x |
+x |
|
E |
0.66 - x |
x |
x |
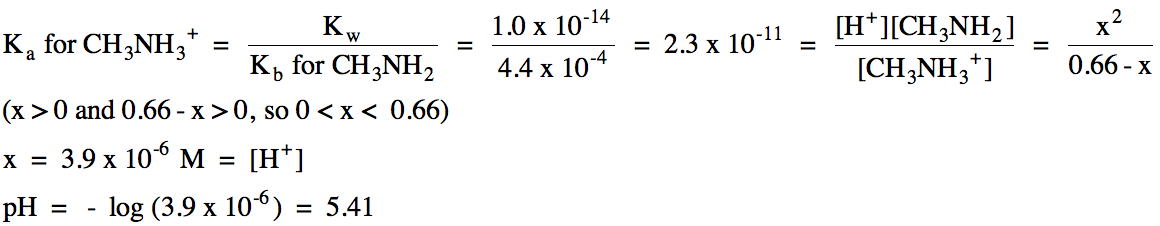
17-18) Predict whether a solution
of potassium hydrogen phosphate, K2HPO4, will be acidic
or basic. Show all relevant
reactions that affect the pH and also give the value of the equilibrium
constant for each reaction you write. For phosphoric acid, H3PO4:
Ka1 = 7.5 x 10-3
Ka2 = 6.2 x 10-8
Ka3 = 4.2 x 10-13
Click for Solution
17-18)
K+ = spectator ion
weak acid
ionization reaction:
HPO42- (aq) ⇌ H+ (aq) + PO43- (aq)
Ka for HPO42- = Ka3 for H3PO4 = 4.2 x 10-13
weak base
hydrolysis reaction:
HPO42- (aq) + H2O (l) ⇌ H2PO4- (aq) + OH- (aq)
Kb for HPO42- = 1.0 x 10-14/(Ka for H2PO4- = Ka2 for H3PO4 = 6.2 x 10-8) = 1.6
x 10-7
Ka < Kb = solution is basic
17-19) Will
the reaction of Cl2O7 and water produce HClO3
or HClO4? Write a
balanced equation for the reaction.
Click for Solution
17-19) The
reaction of Cl2O7 (oxidation number of Cl = +7) and water will produce HClO4 (oxidation
number of Cl = +7) rather than HClO3
(oxidation number of Cl = +5). The balanced equation will be Cl2O7
+ H2O → 2 HClO4.
17-20)
a. An unknown monoprotic
weak acid was found to be 14.13% carbon, 1.78% hydrogen, and 74.67% iodine by
mass, with the remainder being oxygen.
Determine the empirical formula of the acid.
b. In a separate experiment, 9.03
grams of the acid was dissolved in 35 mL of water and
then titrated with 0.414 M calcium hydroxide. The volume of base required to reach the equivalence point
was 32.1 mL.
Calculate the molar mass and determine the molecular formula of the
acid.
Click for Solution
17-20) a.
100% - 14.13% C – 1.78% H - 74.67% I = 9.42% O by mass
Assume one
hundred grams of unknown acid:
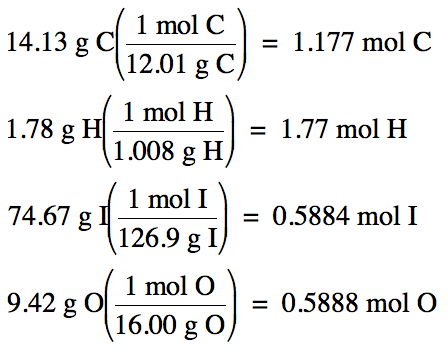
1.177 mol
C: 1.77 mol H: 0.5884 mol I: 0.5888 mol O (divide each by 0.5884)
= 2 mol C:
3 mol H: 1 mol I: 1 mol O
Therefore,
empirical formula is C2H3IO.
b. 0.414 M Ca(OH)2
→ 0.414 M Ca2+
and 2 x 0.414 M = 0.828 M OH-
HA (aq) + OH- (aq) → H2O (l) + A-
(aq)
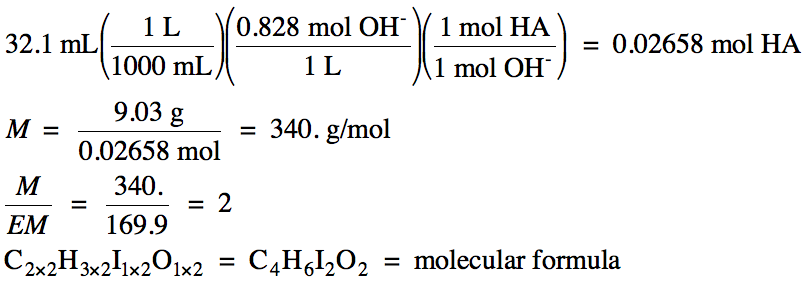
Since the acid is monoprotic, we can rewrite the molecular formula as HC4H5I2O2.
17-21) Calculate the initial molarity of a potassium acetate, KC2H3O2, solution that has a pH of 8.91 given that Ka = 1.8 x 10-5 for acetic acid, HC2H3O2.
Click for Solution
17-21) K+ = spectator
ion, C2H3O2- hydrolyzes as a weak
base:
R
|
C2H3O2- (aq) + H2O(l) ⇌ HC2H3O2 (aq) + OH- (aq)
|
|||
I
|
Mi
|
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
|
E
|
Mi - x
|
x
|
x
|
|
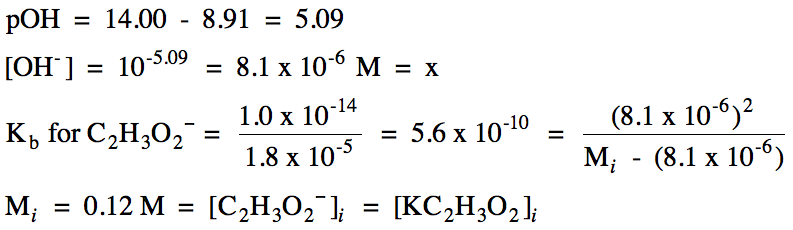
17-22) Calculate the initial
molarity of a CH3NH3Cl [composed of CH3NH3+ and Cl-] solution that has a pH of 5.85 given that Kb =
4.4 x 10-4 for CH3NH2.
Click for Solution
17-22) Cl- = spectator
ion, CH3NH3+ hydrolyzes as a weak acid:
R
|
CH3NH3+ (aq) ⇌ H+ (aq) + CH3NH2 (aq)
|
||
I
|
Mi
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
E
|
Mi - x
|
x
|
x
|

17-23) Given that a 1.6 M NaCN solution has a pH of 11.76, calculate Ka and pKa for HCN.
Click for Solution
17-23) Na+ = spectator
ion, CN- hydrolyzes as a weak base:
R
|
CN- (aq) + H2O(l) ⇌ HCN (aq) + OH- (aq)
|
|||
I
|
1.6
|
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
|
E
|
1.6 - x
|
x
|
x
|
|
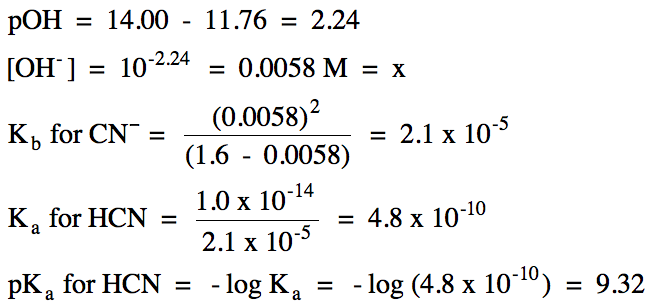
17-24) Given that a 0.87 M C6H5NH3Br
[composed of C6H5NH3+ and Br-]
solution has a pH of 2.35, calculate Kb and pKb for C6H5NH2.
Click for Solution
17-24) Br- = spectator
ion, C6H5NH3+ hydrolyzes as a weak
acid:
R
|
C6H5NH3+ (aq) ⇌ H+ (aq) + C6H5NH2 (aq)
|
||
I
|
0.87
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
E
|
0.87 - x
|
x
|
x
|
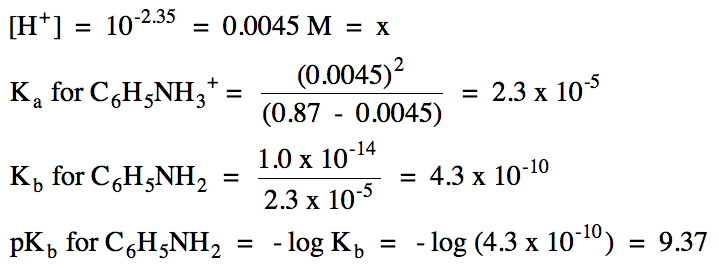
17-25) Calculate the pH of a
solution containing 6.5 grams of KC2H3O2 in
50. mL of 0.88 M HC2H3O2 (Ka = 1.8
x 10-5).
Click for Solution
K+ = spectator ion, HC2H3O2/C2H3O2- = buffer solution:
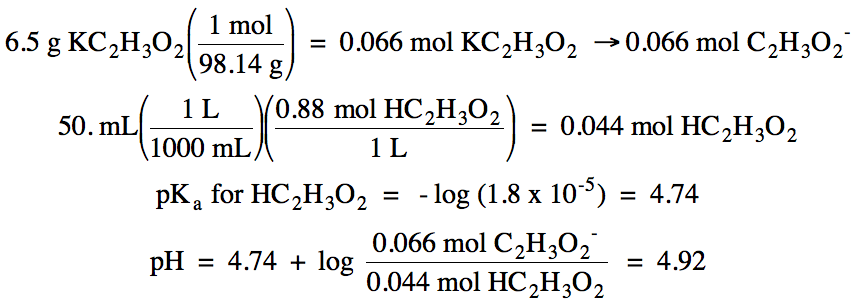
17-26) Calculate the pH of a
solution containing 8.5 grams of CH3NH3Br [composed of CH3NH3+ and Br-] in 88 mL of
0.92 M CH3NH2 (Kb = 4.4 x 10-4).
Click for Solution
Br- = spectator ion, CH3NH2/CH3NH3+ = buffer solution:
17-27) Write the net ionic equation
for the neutralization reaction that occurs and calculate the pH when:
a. 0.003 mol HNO3 is
added to the solution in Practice Exercise 17-25
b. 0.003 mol KOH is added to the
solution in Practice Exercise 17-25
c. 0.003 mol HNO3 is
added to the solution in Practice Exercise 17-26
d. 0.003 mol KOH is added to the
solution in Practice Exercise 17-26
Click for Solution
a. NO3- =
spectator ion
neutralization
reaction: C2H3O2- (aq) + H+ (aq) → HC2H3O2 (aq)
pH = 4.74 +
log (0.066 – 0.003) mol C2H3O2-/(0.044
+ 0.003) mol HC2H3O2 = 4.87
b. K+ = spectator ion
neutralization
reaction: HC2H3O2 (aq) + OH- (aq) → C2H3O2- (aq) + H2O (l)
pH = 4.74 +
log (0.066 + 0.003) mol C2H3O2-/(0.044
- 0.003) mol HC2H3O2 = 4.97
c. NO3- =
spectator ion
neutralization
reaction: CH3NH2 (aq) + H+ (aq) → CH3NH3+ (aq)
pOH = 3.36
+ log (0.076 + 0.003) mol CH3NH3+/(0.081 -
0.003) mol CH3NH2 = 3.37
pH = 14.00
– 3.37 = 10.63
d. K+ = spectator ion
neutralization
reaction: CH3NH3+ (aq) + OH- (aq) → CH3NH2 (aq)
+ H2O (l)
pOH = 3.36
+ log (0.076 - 0.003) mol CH3NH3+/(0.081 +
0.003) mol CH3NH2 = 3.30
pH = 14.00 – 3.30 = 10.70
17-28) Write the net ionic equation
for the neutralization reaction that occurs in each aqueous mixture below. Which one of the four reactions creates
a buffer solution? For each
mixture, describe the method of calculating the pH of the resulting solution
after the neutralization reaction is complete.
a. 0.5 mol KOH + 0.5 mol NH4I
b. 0.2 mol HClO4 + 0.5
mol NaC7H5O2
c. 0.2 mol HClO + 0.5 mol NaOH
d. 0.5 mol HNO3 + 0.2
mol C5H5N (a weak base)
Click for Solution
a. K+ and I- = spectator ions
neutralization
reaction: NH4+ (aq) + OH- (aq) → NH3 (aq) + H2O (l)
n of
NH4+ = nOH-: NH3 solution created, pOH = 14.00 - pH calculated
using RICE chart for ionization of weak base NH3
b. ClO4- and
Na+ = spectator ions
neutralization
reaction: C7H5O2- (aq) + H+ (aq) → HC7H5O2 (aq)
n of
C7H5O2- > nH+: HC7H5O2/
C7H5O2- buffer created, pH = pKa + log (n of C7H5O2- excess/n of HC7H5O2 produced)
c. Na+ = spectator ion
neutralization
reaction: HClO (aq) + OH- (aq) → ClO- (aq) + H2O (l)
nHClO < nOH-: OH-/ClO- solution created, pOH = 14.00 – pH = -log [OH-]excess (hydrolysis of ClO- negligible)
d. NO3- =
spectator ion
neutralization
reaction: C5H5N
(aq) + H+ (aq) → C5H5NH+ (aq)
n of C5H5N
< nH+: H+/
C5H5NH+ solution created, pH = -log [H+]excess (hydrolysis of C5H5NH+ negligible)
17-29) a. Write the net ionic
equation for the neutralization reaction that occurs during the titration of 42
mL of 0.15 M KOH with 0.30 M HI and calculate the volume of acid needed to
reach the equivalence point.
b. Calculate the following:
i. the initial pH
ii. the pH after 13 mL of acid has
been added
iii. the pH at the equivalence
point
iv. the pH after 25 mL of acid has been added
Click for Solution
a. K+ and I- = spectator ions, neutralization reaction: OH- (aq) + H+ (aq) → H2O (l)
0.042 L (0.15 mol OH-/1
L) = 0.0063 mol OH- = 0.0063 mol H+ (1 L/0.30 mol H+)
= 0.021 L = 21 mL acid needed
b.
i. pOH = -log (0.15) = 0.82
pH = 14.00 - 0.82 = 13.18
ii. 0.013 L (0.30 mol H+/1
L) = 0.0039 mol H+ added
pOH = -log [(0.0063 - 0.0039) mol
OH- excess/(0.042 + 0.013) L total] = 1.36
pH = 14.00 - 1.36 = 12.64
iii. only H2O present, pH
= 7
iv. 0.025 L (0.30 mol H+/1
L) = 0.0075 mol H+ added
pH = - log [(0.0075 - 0.0063) mol H+ excess/(0.042 + 0.025) L total] = 1.75
17-30)
a. Write the net ionic equation for
the neutralization reaction that occurs during the titration of 36 mL of 0.20 M
HNO2 (Ka = 4.5 x 10-4) with 0.30 M NaOH and
calculate the volume of base needed to reach the equivalence point.
b. Calculate the following:
i. the initial pH
ii. the pH after 11 mL of base has
been added
iii. the pH at the equivalence
point
iv. the pH after 33 mL of base has
been added
Click for Solution
a. Na+ = spectator ion,
neutralization reaction: HNO2 (aq) + OH- (aq) → H2O
(l) + NO2- (aq)
0.036 L (0.20 mol HNO2/1
L) = 0.0072 mol HNO2 = 0.0072 mol OH- (1 L/0.30 mol OH-)
= 0.024 L = 24 mL base needed
b.
i.
R
|
HNO2 (aq) ⇌ H+ (aq) + NO2- (aq)
|
||
I
|
0.20
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
E
|
0.20 - x
|
x
|
x
|
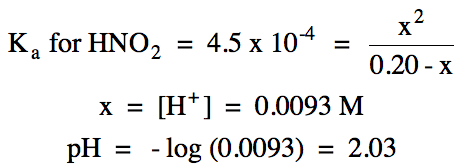
ii.
0.011 L (0.30 mol OH-/1 L) = 0.0033 mol OH- added =
0.0033 mol HNO2 reacted = 0.0033 mol NO2- produced
0.0072 mol
HNO2 initial - 0.0033 mol HNO2 reacted = 0.0039 mol HNO2 excess
pKa for HNO2 = -log (4.5 x 10-4) = 3.35
pH = 3.35 + log (0.0033 mol NO2-/0.0039 mol HNO2) = 3.28
iii.
R
|
NO2- (aq) + H2O(l) ⇌ HNO2 (aq) + OH- (aq)
|
|||
I
|
Mi
|
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
|
E
|
Mi - x
|
x
|
x
|
|
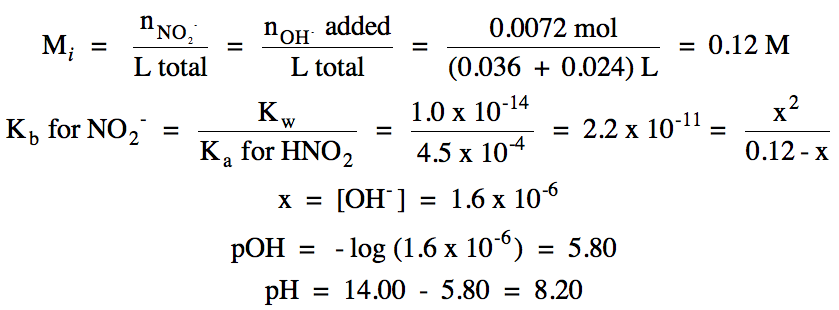
iv. 0.033 L (0.30 mol OH-/1
L) = 0.0099 mol OH- added
pOH = - log [(0.0099 - 0.0072) mol
OH- excess/(0.036 + 0.033) L total] = 1.41
pH = 14.00 – 1.41 = 12.59
17-31)
a. Write the net ionic equation for
the neutralization reaction that occurs during the titration of 18 mL of 0.30 M
CH3NH2 (Kb = 4.4 x 10-4) with 0.20
M HBr and calculate the volume of acid needed to reach the equivalence point.
b. Calculate the following:
i. the initial pH
ii. the pH after 16 mL of acid has
been added
iii. the pH at the equivalence
point
iv. the pH after 38 mL of acid has
been added
Click for Solution
a. Br- = spectator ion,
neutralization reaction: CH3NH2 (aq) + H+ (aq) → CH3NH3+ (aq)
0.018 L (0.30 mol NH3/1
L) = 0.0054 mol CH3NH2 = 0.0054 mol H+ (1
L/0.20 mol H+) = 0.027 L = 27 mL acid needed
b.
i.
R
|
CH3NH2 (aq) + H2O(l) ⇌ CH3NH3+ (aq) + OH- (aq)
|
|||
I
|
0.30
|
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
|
E
|
0.30 - x
|
x
|
x
|
|
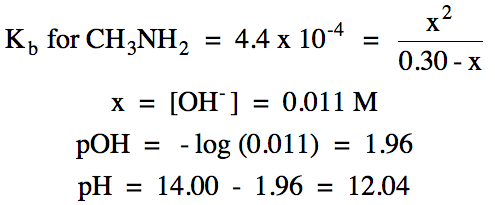
ii.
0.016 L (0.20 mol H+/1 L) = 0.0032 mol H+ added =
0.0032 mol CH3NH2 reacted = 0.0032 mol CH3NH3+ produced
0.0054 mol
CH3NH2 initial - 0.0032 mol CH3NH2 reacted = 0.0022 mol CH3NH2 excess
pKb for CH3NH2 = -log (4.4 x 10-4) = 3.36
pOH = 3.36 + log (0.0032 mol CH3NH3+/0.0022 mol CH3NH2) = 3.52
pH = 14.00 – 3.52 = 10.48
iii.
R
|
CH3NH3+ (aq) ⇌ H+ (aq) + CH3NH2 (aq)
|
||
I
|
Mi
|
0
|
0
|
C
|
-x
|
+x
|
+x
|
E
|
Mi - x
|
x
|
x
|
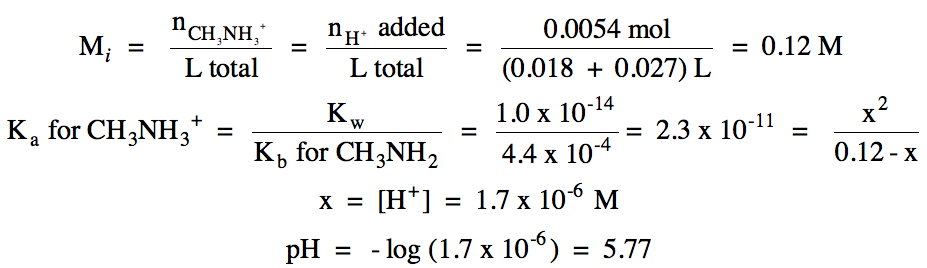
iv. 0.038 L (0.20 mol H+/1
L) = 0.0076 mol H+ added
pH = - log [(0.0076 - 0.0054) mol H+ excess/(0.018 + 0.038) L total] = 1.41
17-32) Which indicator, metacresol
purple (Ka = 5 x 10-9) or 2,4-dinitrophenol (Ka = 1 x 10-4), would be the better choice for the titration in
Practice Exercise 17-30?
Click for Solution
pH at
equivalence point = 8.20
pKa for metacresol purple = -log (5 x 10-9) = 8.3
pKa for 2,4-dinitrophenol = -log (1 x 10-4) = 4.0
pKa for metacresol purple close to pH at equivalence point, so metacresol purple is
better choice
