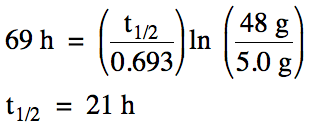Chapter 20: Nuclear Chemistry

Section 20-1: Balancing Nuclear Equations

Section 20-2: Nuclear Kinetics and Half-Life

Chapter 20 Practice Exercises and Review Quizzes

Section 20-1: Balancing Nuclear Equations

During a nuclear reaction, the nuclei of the isotopes involved will undergo a change in composition. Each particle involved in a nuclear reaction will be represented as follows, where Z is the atomic number and A is the mass number:

When a nuclear reaction is balanced, the sum of the Z values for the reactants must equal the sum of the Z values for the products. Likewise, the sum of the A values for the reactants must equal the sum of the A values for the products. Note that charges are typically omitted when nuclear reactions are written.

Types of radioactive decay include:

A. Alpha decay (or alpha emission) = nucleus of an isotope X emits a helium-4 nucleus to produce a new isotope Y. The equation is balanced as follows:

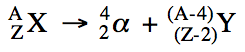
B. Beta decay (or beta emission) = nucleus of an isotope X emits a particle equivalent to an electron to produce a new isotope Y. The equation is balanced as follows:

C. Positron decay (or positron emission) = nucleus of an isotope X emits a particle equivalent to an electron, but with a positive charge, to produce a new isotope Y. The equation is balanced as follows:

D. Electron capture = electron from an inner orbital is absorbed into the nucleus of isotope X to produce a new isotope Y. The equation is balanced as follows:

In each case above, the identity of the isotope Y can be determined by matching the atomic number of Y with an element on the periodic table:

Sample Exercise 20A:

Write balanced equations for the following nuclear reactions:

a. Uranium-235 decays by alpha emission.

b. Rubidium-87 decays by beta emission.

c. Potassium-38 decays by positron emission.

d. Iron-55 decays by electron capture.

Solution:

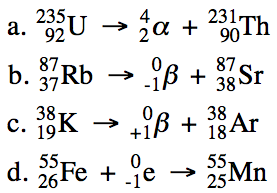
A nuclear reaction may also be initiated by bombarding a sample of an isotope with particles such as neutrons or protons in order to produce a new isotope. Other particles may be produced in the process as well. The symbols for a neutron and a proton are as follows:

Sample Exercise 20B:

Neutron bombardment of nitrogen-14 produces a proton and a new isotope. Write a balanced equation for this nuclear reaction.

Solution:

Section 20-2: Nuclear Kinetics and Half-Life

Radioactive decay is first-order. Given the initial quantity (Q_i) of a radioactive isotope in any unit (such as grams, moles, or number of atoms), the final quantity (Q_f) can be calculated using the following equation:

ln Q_f = -kt + ln Q_i

The half-life (t_1/2) of a radioactive isotope is the time required for the isotope to decay to half its initial quantity. Using the equation above, we can derive the relationship between half-life and the rate constant k by substituting 0.5Q_i for Q_fand t_1/2for t:

ln (0.5Q_i) = -kt_1/2+ ln Q_i

kt_1/2= ln (Q_i /0.5Q_i) = ln 2

t_1/2= ln 2/k = 0.693/k and k = 0.693/t_1/2

Replacing k with 0.693/t_1/2 in the equation ln Q_f = -kt + ln Q_i, we obtain the following equation:

ln Q_f = -(0.693/t_1/2)t + ln Q_i

Sample Exercise 20C:

The half-life of bromine-80 is 18 minutes. What mass of bromine-80 will remain if a 96 gram sample decays for 25 minutes?

Solution:

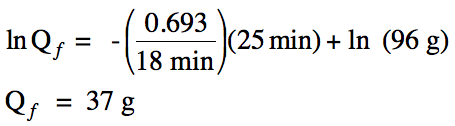
If the equation ln Q_f = -(0.693/t_1/2)t + ln Q_i is solved for t, we obtain:

t = (t_1/2/0.693)ln (Q_i/Q_f)

Sample Exercise 20D:

The half-life of potassium-40 is 1.25 x 10⁹ years. How much time is required for a 9.48 mol sample of potassium-40 to decay to 1.22 mol?

Solution:

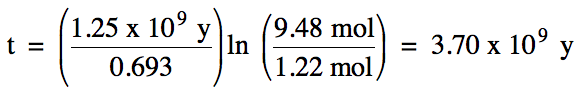
We can also solve for t_1/2 as follows:

Sample Exercise 20E:

A sample of radon-222 containing 6.54 x 10²⁵ atoms requires 17.6 days to decay to 2.66 x 10²⁴ atoms. Calculate the half-life of radon-222.

Solution:

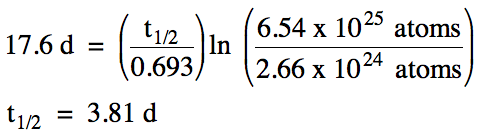
Chapter 20 Practice Exercises and Review Quizzes:

20-1) Write balanced equations for the following nuclear reactions:

a. Lead-196 decays by electron capture.

b. Phosphorus-28 decays by positron emission.

c. Radium-226 decays by alpha emission.

d. Zinc-73 decays by beta emission.

Click for Solution

20-1)

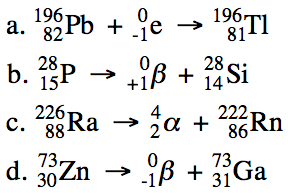
20-2) Proton bombardment of magnesium-26 produces an alpha particle and a new isotope. Write a balanced equation for this nuclear reaction.

Click for Solution

20-2)

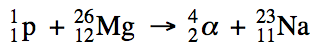
20-3) The half-life of oxygen-13 is 0.00870 seconds. How many moles of oxygen-13 will remain if a 38.4 mol sample decays for 0.0125 seconds?

Click for Solution

20-3)

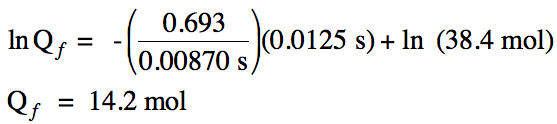
20-4) The half-life of iodine-131 is 8.04 days. How much time is required for a sample containing 6.56 x 10²³ iodine-131 atoms to decay to 1.26 x 10²³ atoms?

Click for Solution

20-4)

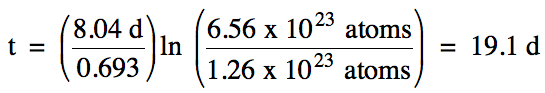
20-5) A 48 gram sample of magnesium-28 requires 69 hours to decay to 5.0 grams. Calculate the half-life of magnesium-28.

Click for Solution

20-5)

Click for Review Quiz 1

Click for Review Quiz 1 Answers