Chapter 21: Colligative Properties

Section 21-2: Freezing Point Depression, Boiling Point Elevation, and the van't Hoff Factor

Section 21-3: Experiment - Determining Molar Mass Using Freezing Point Depression

Section 21-4: Raoult's Law and Vapor Pressure

Chapter 21 Practice Exercises and Review Quizzes

Section 21-1: Molality

Molality (m) is another way to express the concentration of a solution and is found by dividing the moles of solute by the kilograms of solvent:

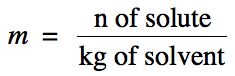
Sample Exercise 21A:

Calculate the molality of a solution containing 17 grams of glucose, C₆H₁₂O₆, dissolved in 225 grams of water.

Solution:

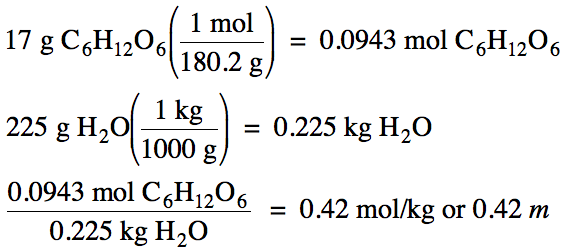
Molality in mol/kg can be used a conversion factor between moles of solute and kilograms of solvent:

Sample Exercise 21B:

Calculate the mass of I₂ that must be dissolved in 115 grams of carbon disulfide to create a 0.097 m solution.

Solution:

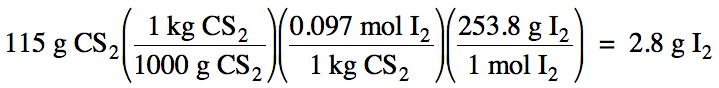
Sample Exercise 21C:

To create a 0.105 m solution, how many grams of cyclohexane, C₆H₁₂, must be used to dissolve 12.6 grams of C₆H₄Cl₂?

Solution:

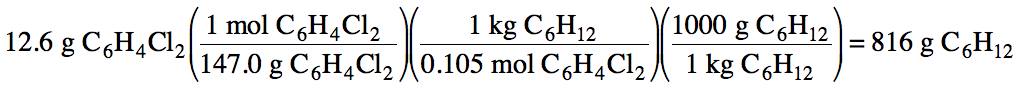
Section 21-2: Freezing Point Depression, Boiling Point Elevation, and the van't Hoff Factor

Colligative properties of solutions, such as freezing point depression and boiling point elevation, depend on the concentration of solute particles, but not on the identity of the solute particles. When a solute is dissolved in a solvent, the freezing point (t_f) of the solution will be lower than the freezing point of the pure solvent, and the boiling point (t_b) of the solution will be higher than the boiling point of the pure solvent.

The magnitude of the freezing point depression (Δt_f), or difference between the freezing points of the pure solvent and the solution, can be calculated using the following equation if the solute is molecular and does not ionize:

Δt_f = K_fm

The magnitude of the boiling point elevation (Δt_b), or difference between the boiling points of the solution and the pure solvent, can be calculated using the following equation if the solute is molecular and does not ionize:

Δt_b = K_bm

The freezing point depression constant K_f and the boiling point elevation constant K_b (not to be confused with base ionization constant) have the unit °C/m and will be different for each solvent. The freezing point depression can be subtracted from the freezing point of the pure solvent to find the freezing point of the solution. The boiling point elevation can be added to the boiling point of the pure solvent to find the boiling point of the solution:

Sample Exercise 21D:

The freezing point of water is 0.0°C and the boiling point of water is 100.0°C. Given that K_f = 1.86°C/m and K_b = 0.52°C/m for water, calculate the freezing and boiling points of a solution containing 33 grams of sucrose, C₁₂H₂₂O₁₁, dissolved in 46 grams of water.

Solution:

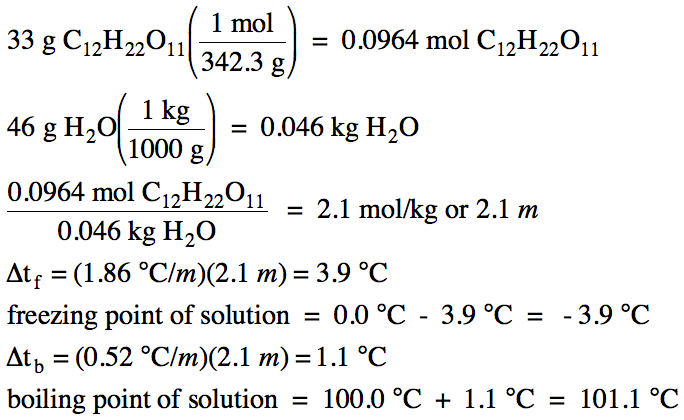
If the solute ionizes to some extent during the dissolving process, the resulting concentration of solute particles will be larger compared to a solution with the same molality in which the solute is molecular and does not ionize. For solutions in which some or all of the solute is ionized, the following equations can be used to calculate the freezing point depression and boiling point elevation:

Δt_f = iK_fm Δt_b = iK_bm

The van’t Hoff factor i indicates the degree to which a solute ionizes in water as follows:

Type of Compound	Value of i
molecular (no ionization)	1
monoprotic weak acid	1 < i < 2
monoprotic strong acid	2
ionic	i = # ions in formula unit

Sample Exercise 21E:

Rank the following aqueous solutions in order from lowest to highest freezing point and from lowest to highest boiling point without performing detailed calculations:

0.010 m C₆H₁₂O₆

0.010 m HF

0.010 m Na₃PO₄

0.011 m MgI₂

0.015 m HCl

Solution:

Each solution has the same solvent and, therefore, will have the same value of K_f in the equation Δt_f = iK_fm and the same value of K_b in the equation Δt_b = iK_bm. As such, a solution with a larger product of (i x m) will have a larger freezing point depression and a larger boiling point elevation. The solutions can be ranked from smallest Δt_f and Δt_b at the top to largest Δt_fand Δt_b at the bottom as follows:

0.010 m C₆H₁₂O₆ = molecular (no ionization), i = 1: i x m = 1 x 0.010 m = 0.010 m

0.010 m HF = monoprotic weak acid, 1 < i < 2: 0.010 m < i x m < 0.020 m

0.015 m HCl = monoprotic strong acid, i = 2 (H⁺ + Cl^-): i x m = 2 x 0.015 m = 0.030 m

0.011 m MgI₂ = ionic, i = 3 (Mg²⁺ + 2 I^-): i x m = 3 x 0.011 m = 0.033 m

0.010 m Na₃PO₄ = ionic, i = 4 (3 Na⁺ + PO₄^3-): i x m = 4 x 0.010 m = 0.040 m

A solution with a larger Δt_fwill have a lower freezing point. Therefore, the solutions will be ranked from lowest to highest freezing point as follows:

0.010 m Na₃PO₄ < 0.011 m MgCl₂ < 0.015 m HCl < 0.010 m HF < 0.010 m C₆H₁₂O₆

A solution with a larger Δt_b will have a higher boiling point. Therefore, the solutions will be ranked from lowest to highest boiling point as follows:

0.010 m C₆H₁₂O₆ < 0.010 m HF < 0.015 m HCl < 0.011 m MgI₂ < 0.010 m Na₃PO₄

Section 21-3: Experiment - Determining Molar Mass Using Freezing Point Depression

The molar mass of a molecular solute that does not ionize (i = 1) can be determined using freezing point depression as follows:

1. Measure the mass of the solute.

2. Measure the mass and freezing point of the pure solvent.

3. Dissolve the solute and measure the freezing point of the resulting solution.

4. Given the K_f value for the solvent expressed in the unit °C•kg/mol, solve for moles of solute in the freezing point depression equation Δt_f = K_f(n_solute/kg solvent).

5. Divide the grams of solute by the moles of solute to obtain the molar mass of the solute.

If we have determined the empirical formula of the solute, we can use the molar mass we have calculated to determine the molecular formula of the solute as follows:

Sample Exercise 21F:

A molecular solute that does not ionize has the empirical formula C₅H₄. A solution containing 1.48 grams of the solute dissolved in 55.7 grams of benzene was found to freeze at 4.47°C. If K_f for benzene is 5.12°C/m and the freezing point of pure benzene is 5.53°C, determine the molar mass and molecular formula of the solute.

Solution:

Section 21-4: Raoult’s Law and Vapor Pressure

The vapor pressure above a pure liquid A can be denoted P_A°. After a solute is dissolved in A, the vapor pressure of A above the solution, P_A, will be lower than P_A°. If we focus only on solutes that are molecular and do not ionize, the following version of Raoult’s Law can be used to calculate the vapor pressure of A above a solution (where x_A = mole fraction of A in solution):

P_A = x_AP_A° = (n_A/n_total)P_A°

If the solute is nonvolatile (has a negligible vapor pressure and, therefore, does not add to the total vapor pressure above the solution), then the total vapor pressure, P_total, above the solution will be equal to P_A calculated using Raoult’s Law:

Sample Exercise 21G:

The vapor pressure of pure water at 22°C is 19.8 mmHg. Calculate the vapor pressure of water and the total vapor pressure above a solution containing 205 grams of nonvolatile sucrose, C₁₂H₂₂O₁₁, dissolved in 575 grams of water at 22°C.

Solution:

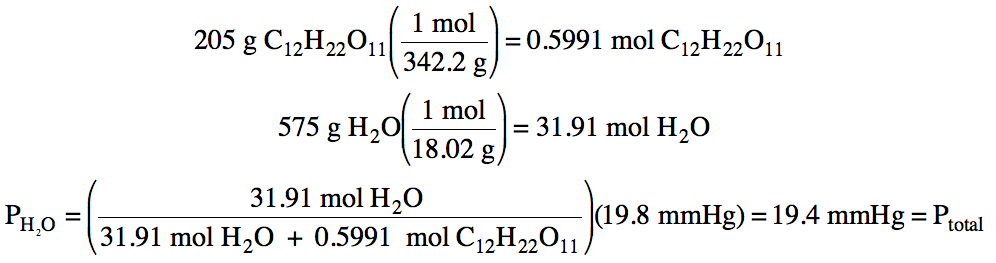
To determine the total vapor pressure above a mixture of two volatile liquids A and B, Raoult’s Law must be used twice to calculate the partial vapor pressures P_A and P_B above the mixture, after which P_A and P_B can be added to obtain the total vapor pressure above the mixture. The mole fraction of A in the vapor, x_{A (g)}, will be equal to the ratio of the partial vapor pressure of A to the total vapor pressure, as shown below:

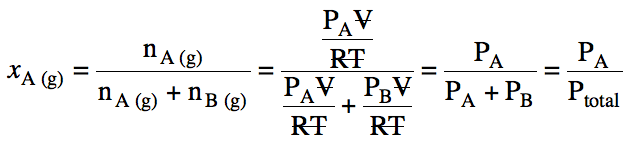
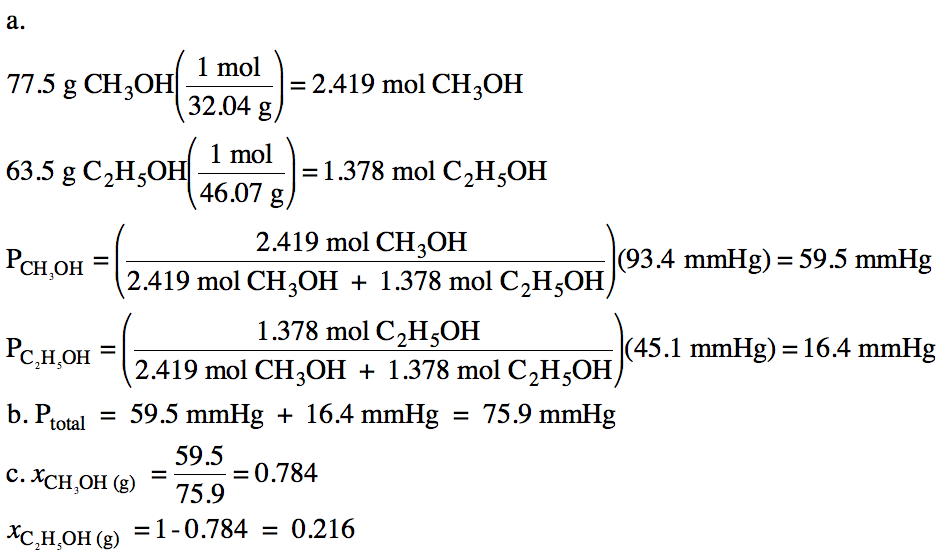
Sample Exercise 21H:

The vapor pressure of pure methanol, CH₃OH, at 21°C is 93.4 mmHg. The vapor pressure of pure ethanol, C₂H₅OH, at 21°C is 45.1 mmHg. For a liquid mixture containing 77.5 grams of methanol and 63.5 grams of ethanol at 21°C, calculate:

a. The partial vapor pressures of methanol and ethanol above the mixture.

b. The total vapor pressure above the mixture.

c. The mole fractions of methanol vapor and ethanol vapor above the mixture.

Solution:

Chapter 21 Practice Exercises and Review Quizzes:

21-1) Calculate the mass of naphthalene, C₁₀H₈, that must be dissolved in 175 grams of chloroform, CHCl₃, to create a 1.2 m solution.

Click for Solution

21-1)

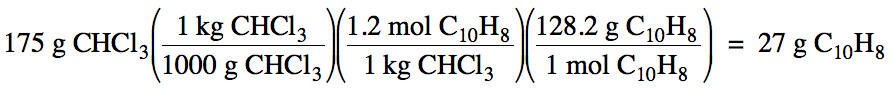
21-2) To create a 0.0855 m solution, how many grams of methanol must be used to dissolve 0.548 grams of benzoic acid, C₆H₅COOH?

Click for Solution

21-2)

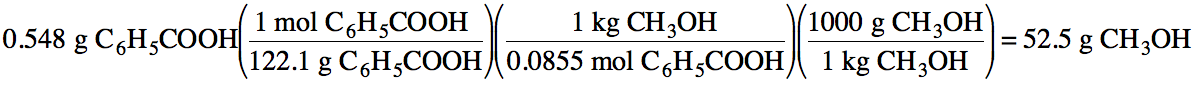
21-3) The freezing point of cyclohexane, C₆H₁₂, is 6.6°C and the boiling point of cyclohexane is 80.7°C. Given that K_f = 20.0°C/m and K_b = 2.79°C/m for cyclohexane, calculate the molality, the freezing point, and the boiling point of a solution containing 18 grams of carbon tetraiodide dissolved in 88 grams of cyclohexane.

Click for Solution

21-3)

21-4) Rank the following aqueous solutions in order from lowest to highest freezing point and from lowest to highest boiling point without performing detailed calculations:

0.013 m CaCl₂

0.014 m C₁₂H₂₂O₁₁

0.014 m HC₂H₃O₂

0.015 m KBr

0.017 m HNO₃

Click for Solution

21-4) Each solution has the same solvent and, therefore, will have the same value of K_f in the equation Δt_f = iK_fm and the same value of K_b in the equation Δt_b = iK_bm. As such, a solution with a larger product of (i x m) will have a larger freezing point depression and a larger boiling point elevation. The solutions can be ranked from smallest Δt_f and Δt_b at the top to largest Δt_fand Δt_b at the bottom as follows:

0.014 m C₁₂H₂₂O₁₁ = molecular (no ionization), i = 1: i x m = 1 x 0.014 m = 0.014 m

0.014 m HC₂H₃O₂ = monoprotic weak acid, 1 < i < 2: 0.014 m < i x m < 0.028 m

0.015 m KBr = ionic, i = 2 (K⁺ + Br^-): i x m = 2 x 0.015 m = 0.030 m

0.017 m HNO₃ = monoprotic strong acid, i = 2 (H⁺ + NO₃^-): i x m = 2 x 0.017 m = 0.034 m

0.013 m CaCl₂ = ionic, i = 3 (Ca²⁺ + 2 Cl^-): i x m = 3 x 0.013 m = 0.039 m

A solution with a larger Δt_fwill have a lower freezing point. Therefore, the solutions will be ranked from lowest to highest freezing point as follows:

0.013 m CaCl₂ < 0.017 m HNO₃ < 0.015 m KBr < 0.014 m HC₂H₃O₂ < 0.014 m C₁₂H₂₂O₁₁

A solution with a larger Δt_b will have a higher boiling point. Therefore, the solutions will be ranked from lowest to highest boiling point as follows:

0.014 m C₁₂H₂₂O₁₁ < 0.014 m HC₂H₃O₂ < 0.015 m KBr < 0.017 m HNO₃ < 0.013 m CaCl₂

21-5) (a) A molecular solute that does not ionize was found to be 30.6% carbon and 1.7% hydrogen by mass, with the remainder being bromine. Determine the empirical formula of the solute.

(b) A solution containing 3.60 grams of the solute dissolved in 33.4 grams of carbon tetrachloride was found to freeze at -36.5°C. If K_f for carbon tetrachloride is 29.8°C/m and the freezing point of pure carbon tetrachloride is -22.9°C, determine the molar mass and molecular formula of the solute.

Click for Solution

21-5) (a) 100% - 30.6% C – 1.7% H = 67.7% Br by mass

Assume one hundred grams of solute:

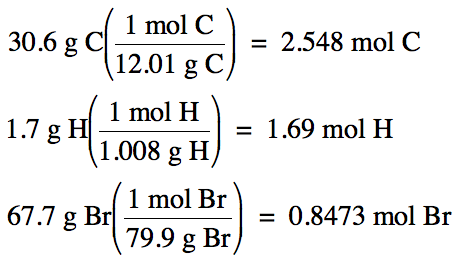
2.548 mol C: 1.69 mol H: 0.8473 mol Br (divide each by 0.8473)

= 3 mol C: 2 mol H: 1 mol Br

C₃H₂Br = empirical formula

(b)

21-6) The vapor pressure of pure water at 35°C is 42.2 mmHg. Calculate the vapor pressure of water and the total vapor pressure above a solution containing 10.0 grams of nonvolatile urea, (NH₂)₂CO, dissolved in 175 grams of water at 35°C.

Click for Solution

21-6)

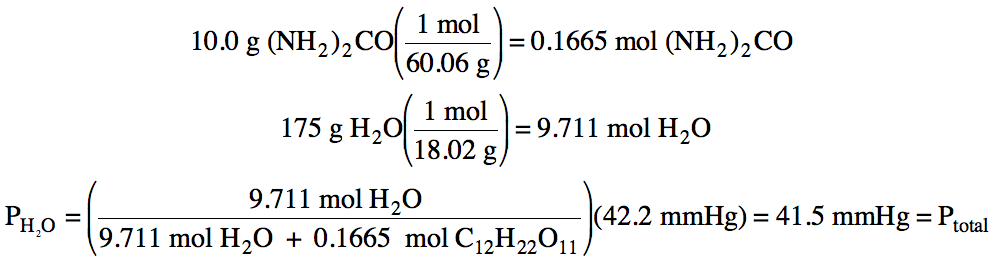
21-7) The vapor pressure of pure benzene, C₆H₆, at 32°C is 129.8 mmHg. The vapor pressure of pure toluene, C₇H₈, at 32°C is 40.5 mmHg. For a liquid mixture containing 265 grams of benzene and 395 grams of toluene at 32°C, calculate:

a. The partial vapor pressures of benzene and toluene above the mixture.

b. The total vapor pressure above the mixture.

c. The mole fractions of benzene vapor and toluene vapor above the mixture.

Click for Solution

21-7)

Click for Review Quiz 1

Click for Review Quiz 1 Answers