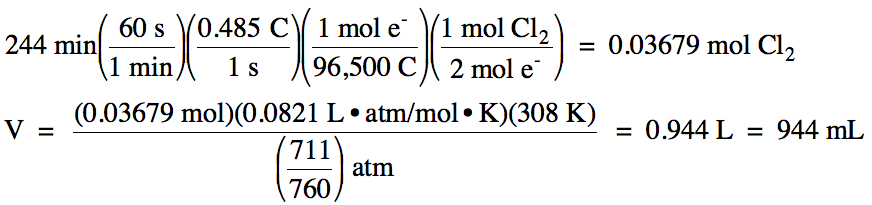Chapter 16: Oxidation-Reduction (Redox) Reactions and Electrochemistry
Section 16-1: Oxidation and Reduction Half-Reactions
Section 16-2: Using Oxidation Numbers to Identify Oxidizing and Reducing Agents
Section 16-3: Balancing Redox Reactions in Aqueous Acidic Solutions
Section 16-5: Calculating E°cell and ΔG° to Determine Spontaneity of Redox Reactions
Section 16-6: Redox Reactions of Metals, Acids, and Halogens
Section 16-7: Experiment - Constructing a Galvanic Cell
Section 16-8: Nonspontaneous Redox Reactions and Electrolysis
Chapter 16 Practice Exercises and Review Quizzes
Section 16-1: Oxidation and Reduction Half-Reactions
The oxidation half-reaction always
shows the electrons lost on the right side of the equation:
oxidation: Zn → Zn2+ + 2e-
The reduction half-reaction always
shows the electrons gained on the left side of the equation:
reduction: Pb2+
+ 2e- → Pb
The overall reaction representing
the sum of the oxidation and reduction half-reactions is known as an
oxidation-reduction or redox reaction. Thus, a redox
reaction involves the transfer of electrons.
Section 16-2: Using Oxidation Numbers to Identify
Oxidizing and Reducing Agents
The reactant in the oxidation
half-reaction that loses electrons is known as the reducing agent. The
reactant in the reduction half-reaction that gains electrons is known as the oxidizing agent. In some redox
reactions, it is not readily apparent which reactant is the oxidizing agent and
which reactant is the reducing agent.
Assigning oxidation numbers (also
known as oxidation states) to each atom in the reactants and products can help
us identify the oxidizing and reducing agents. Oxidation numbers can be integers or fractions. To assign oxidation numbers, use the
following rules:
Rule 1: For a given reactant or product, the sum of the oxidation
numbers for all atoms is equal to the overall charge in the chemical formula.
Rule 2: For neutral monatomic and polyatomic elements, the oxidation
number of each atom is zero. For
example, the oxidation numbers of the iron atom in Fe, each nitrogen atom in N2,
and each sulfur atom in S8 are all zero.
Rule 3: For monatomic ions, the oxidation number is equal to the
charge on the ion. For example,
the oxidation number of aluminum in Al3+ is +3.
Rule 4: For polyatomic ions containing only one element, the
oxidation number of each atom is equal to the charge divided by the number of
atoms. For example, the oxidation
number of each mercury atom in Hg22+ is +1 (+2 divided by
2).
Rule 5: In neutral compounds or polyatomic ions containing more than one
element, oxidation numbers are assigned to each atom as follows:
a. Group 1 metals (does not include
hydrogen) = +1
b. Group 2 metals = +2
c. H = +1
d. F = -1
e. O = -2
f. Group 17 elements = -1
g. Group 16 elements = -2
h. Group 15 elements = -3
i. The oxidation number of elements not
listed above can be determined using a combination of known oxidation numbers and
Rule 1. For example, we know from
Rule 5e that the oxidation number of each oxygen atom in Cr2O72-
is -2. Since Rule 1 specifies that
the sum of the oxidation numbers for all atoms should equal the overall charge
of -2, we can solve the following equation to determine the oxidation number of
each chromium atom:
2(Cr) +
7(-2) = -2
Cr = +6
j. When rules conflict, the rule
higher on this list (closer to top of page) takes priority. For example, SF2 presents a
conflict because Rule 5d specifies that F = -1 and Rule 5g specifies that S =
-2, which does not conform to Rule 1 specifying that the sum of the oxidation
numbers must equal the overall charge of zero. Since Rule 5d specifying that F = -1 takes priority over
Rule 5g, we can solve the following equation to determine the oxidation number
of the sulfur atom:
S + 2(-1) =
0
S = +2
Sample Exercise 16A:
Determine all oxidation numbers in:
a. P4
b. S2-
c. CH2O
d. BrO3-
e. NaO2
Solution:
a. P = 0 (Rule 2)
b. S = -2 (Rule 3)
c. H = +1 (Rule 5c) and O = -2
(Rule 5e)
C + 2(+1) + (-2) = 0
C = 0
d. Conflict: Rule 5e (O = -2) takes priority over
Rule 5f
Br + 3(-2) = -1
Br = +5
e. Conflict: Rule 5a (Na = +1) takes priority over
Rule 5e
(+1) + 2(O) = 0
O = -1/2
Once we have assigned oxidation
numbers to every atom in the reactants and products, we can determine which
reactant is the reducing agent and which reactant is the oxidizing agent as
follows:
reducing agent
(loses electrons) = reactant containing an element that undergoes an increase
in oxidation number (becomes more positive or less negative)
oxidizing agent
(gains electrons) = reactant containing an element that undergoes a decrease in
oxidation number (becomes less positive or more negative)
Reactions during which no elements
undergo a change in oxidation number are not redox
reactions.
Sample Exercise 16B:
Determine all oxidation numbers in
the following unbalanced reactions, and then decide which of the two is a redox reaction.
For the redox reaction, identify the reducing
agent and the oxidizing agent.
a. Na2SO4 +
BaCl2 → BaSO4
+ NaCl
b. VO2+ + F2 → VO2+ + F-
Solution:
Using oxidation number rules in
order of priority:
a. Na2SO4 (Na
= +1, O = -2, S = +6) + BaCl2 (Ba = +2, Cl = -1)→ BaSO4
(Ba = +2, O = -2, S = +6) + NaCl
(Na = +1, Cl = -1)
Since no elements undergo a change
in oxidation number, this is not a redox reaction.
b. VO2+ (O = -2, V = +4)
+ F2 (F = 0) → VO2+
(O = -2, V = +5) + F- (F = -1)
Since oxidation numbers change,
this is a redox reaction. VO2+ contains the element V that undergoes an
increase in oxidation number from +4 to +5, so VO2+ is the reducing
agent. F2 contains the
element F that undergoes a decrease in oxidation number from 0 to -1, so F2
is the oxidizing agent.
Section 16-3: Balancing Redox
Reactions in Aqueous Acidic Solutions
Redox reactions
that occur in aqueous acidic solutions can be balanced by not only changing
coefficients, but also by adding hydrogen ions (H+) and water
molecules into the reaction. The
steps required will be demonstrated in order while balancing the following
equation using the smallest possible whole-number coefficients:
H2C2O4
+ NO3- → CO2
+ NO
Step 1: Determine all oxidation numbers in the unbalanced equation, then identify the reducing agent and the oxidizing agent.
H2C2O4
(H = +1, O = -2, C = +3) + NO3- (O = -2, N = +5) → CO2 (O = -2, C = +4) +
NO (O = -2, N = +2)
H2C2O4
contains the element C that undergoes an increase in oxidation number from +3
to +4, so H2C2O4 is the reducing agent. NO3- contains the
element N that undergoes a decrease in oxidation number from +5 to +2, so NO31-
is the oxidizing agent.
Step 2: Write the unbalanced oxidation half-reaction and the
unbalanced reduction half-reaction.
The reducing agent is always the reactant on the left side of the
oxidation half-reaction, and the oxidizing agent is always the reactant on the
left side of the reduction half-reaction.
The product on the right side of each half-reaction must contain the
same element that underwent a change in oxidation number as the reactant in
that same half-reaction:
oxidation: H2C2O4
→ CO2
reduction: NO3-
→ NO
Step 3: Change coefficients as necessary to balance all elements
except oxygen and hydrogen:
oxidation: H2C2O4
→ 2
CO2
reduction: NO3-
→ NO
Step 4: Balance oxygen by adding H2O molecules as
necessary to the deficient side:
oxidation: H2C2O4
→ 2 CO2
reduction: NO3-
→ NO + 2
H2O
Step 5: Balance hydrogen by adding H+ ions as necessary
to the deficient side:
oxidation: H2C2O4
→ 2 CO2
+ 2 H+
reduction: NO3-
+ 4 H+ → NO + 2 H2O
Step 6: Add enough electrons to the right side of the oxidation
half-reaction and the left side of the reduction half-reaction to ensure that
the total charge is equal on both sides of each half-reaction. The total charge on each side of a
half-reaction can be determined by finding the sum of (coefficient x charge)
for all reactants or products on that side of the equation:
oxidation: H2C2O4
→ 2 CO2
+ 2 H+ + 2 e- (total charge on left = 1 x 0 = 0,
total charge on right = 2 x 0 + 2 x 1 + 2 x -1 = 0)
reduction: NO3-
+ 4 H+ + 3 e- → NO + 2 H2O
(total charge on left = 1 x -1 + 4 x 1 + 3 x -1 = 0, total charge on right = 1
x 0 + 2 x 0 = 0)
Step 7: Determine the least common multiple (LCM) of the electron
coefficients in each half-reaction.
Multiply all the coefficients in each half-reaction by an integer that
will give both half-reactions an electron coefficient equal to the LCM:
LCM of
electron coefficients 2 and 3 = 6
oxidation: (H2C2O4
→ 2 CO2
+ 2 H+ + 2 e-) x 3
= 3 H2C2O4
→ 6 CO2
+ 6 H+ + 6 e-
reduction: (NO3-
+ 4 H+ + 3 e- → NO + 2 H2O)
x 2
= 2 NO3-
+ 8 H+ + 6 e- → 2 NO + 4 H2O
Step 8: Add the two half-reactions to obtain the overall balanced
equation, which should no longer contain electrons and should have the same
total charge on both sides:
3 H2C2O4
+ 2 NO3- + 8 H+ + 6e- → 6 CO2 + 6 H+
+ 6 e- + 2 NO + 4 H2O
overall balanced equation: 3 H2C2O4
+ 2 NO3- + 2 H+ → 6 CO2 + 2 NO + 4 H2O
(total charge on left = 3 x 0 + 2 x -1 + 2 x 1 = 0, total
charge on right = 6 x 0 + 2 x 0 + 4 x 0 = 0)
Sample Exercise 16C:
Determine all oxidation numbers,
identify the reducing agent and oxidizing agent, and balance the following
equation that occurs in aqueous acidic solution using the smallest possible
whole-number coefficients:
Cr2O72-
+ I2 → Cr3+
+ IO3-
Solution:
Step 1:
Cr2O72-
(O = -2, Cr = +6) + I2 (I = 0) → Cr3+
(Cr = +3) + IO3- (O = -2, I = +5)
reducing agent = I2 (oxidation number of I
increases from 0 to +5)
oxidizing agent = Cr2O72-
(oxidation number of Cr decreases from +6 to +3)
Step 2:
oxidation: I2
→ IO3-
reduction: Cr2O72-
→ Cr3+
Step 3:
oxidation: I2
→ 2 IO3-
reduction: Cr2O72-
→ 2 Cr3+
Step 4:
oxidation: I2
+ 6 H2O → 2 IO3-
reduction: Cr2O72-
→ 2 Cr3+
+ 7 H2O
Step 5:
oxidation: I2
+ 6 H2O → 2 IO3-
+ 12 H+
reduction: Cr2O72-
+ 14 H+ → 2 Cr3+
+ 7 H2O
Step 6:
oxidation: I2
+ 6 H2O → 2 IO3-
+ 12 H+ + 10 e-
reduction: Cr2O72-
+ 14 H+ + 6 e- → 2 Cr3+
+ 7 H2O
Step 7: LCM of electron coefficients 10 and 6 = 30
oxidation: (I2
+ 6 H2O → 2 IO3-
+ 12 H+ + 10 e-) x 3
= 3 I2
+ 18 H2O → 6 IO3-
+ 36 H+ + 30 e-
reduction: (Cr2O72-
+ 14 H+ + 6 e- → 2 Cr3+
+ 7 H2O) x 5
= 5 Cr2O72-
+ 70 H+ + 30 e- → 10 Cr3+
+ 35 H2O
Step 8:
3 I2
+ 18 H2O + 5 Cr2O72- + 70 H+
+ 30 e- → 6 IO3-
+ 36 H+ + 30 e- + 10 Cr3+ + 35 H2O
overall balanced equation: 3 I2 + 5 Cr2O72-
+ 34 H+ → 6 IO3-
+ 10 Cr3+ + 17 H2O
(total charge on left = 3 x 0 + 5 x -2 + 34 x 1 = +24, total
charge on right = 6 x -1 + 10 x 3 + 17 x 0 = +24)
To balance redox
reactions that do not involve oxygen or hydrogen, omit Step 4 and Step 5 from
the method above.
Section 16-4: Using a Standard Reduction Potentials
Table to Compare Strengths of Oxidizing and Reducing Agents
The table of standard reduction
potentials (E°red) in the unit volts (V) shown below can be used to
compare the relative tendency of reduction half-reactions to occur under
standard conditions (all aqueous reactants and products having a concentration
of 1 M and all gaseous reactants and products having a partial pressure of 1
atm):
Half-Reaction
|
E°red (V)
|
F2 (g) + 2 e-→ 2 F- (aq)
|
+2.87
|
Co3+ (aq) + 1 e-→ Co2+ (aq)
|
+1.82
|
Au3+ (aq) + 3 e-→ Au (s)
|
+1.50
|
Cl2 (g) + 2 e-→ 2 Cl- (aq)
|
+1.36
|
O2 (g) + 4 H+ (aq) + 4 e-→ 2 H2O (l)
|
+1.23
|
Br2 (l) + 2 e-→ 2 Br- (aq)
|
+1.07
|
NO3- (aq) + 4 H+ (aq) + 3 e-→ NO (g) + 2 H2O (l)
|
+0.96
|
Ag+ (aq) + 1 e-→ Ag (s)
|
+0.80
|
Fe3+ (aq) + 1 e-→ Fe2+ (aq)
|
+0.77
|
I2 (s) + 2 e-→ 2 I- (aq)
|
+0.53
|
Cu2+ (aq) + 2 e-→ Cu (s)
|
+0.34
|
Sn4+ (aq) + 2 e-→ Sn2+ (aq)
|
+0.15
|
2 H+ (aq) + 2 e-→ H2 (g)
|
0
|
Pb2+ (aq) + 2 e-→ Pb (s)
|
-0.13
|
Sn2+ (aq) + 2 e-→ Sn (s)
|
-0.14
|
Ni2+ (aq) + 2 e-→ Ni (s)
|
-0.25
|
V3+ (aq) + 1 e-→ V2+ (aq)
|
-0.26
|
Co2+ (aq) + 2 e-→ Co (s)
|
-0.28
|
Cd2+ (aq) + 2 e-→ Cd (s)
|
-0.40
|
Fe2+ (aq) + 2 e-→ Fe (s)
|
-0.44
|
Cr3+ (aq) + 3 e-→ Cr (s)
|
-0.74
|
Zn2+ (aq) + 2 e-→ Zn (s)
|
-0.76
|
2 H2O
(l) + 2 e-→ H2 (g) + 2 OH- (aq)
|
-0.83
|
Mn2+ (aq) + 2 e-→ Mn (s)
|
-1.18
|
Al3+ (aq) + 3 e-→ Al (s)
|
-1.66
|
Mg2+ (aq) + 2 e-→ Mg (s)
|
-2.37
|
Na+ (aq) + 1 e-→ Na (s)
|
-2.71
|
Ca2+ (aq) + 2 e-→ Ca (s)
|
-2.87
|
Ba2+ (aq) + 2 e-→ Ba (s)
|
-2.90
|
K+ (aq) + 1 e-→ K (s)
|
-2.92
|
Li+ (aq) + 1 e-→ Li (s)
|
-3.05
|
When E°red is more positive or less negative, the reduction half-reaction will have a greater tendency to occur. This means that the reactant in the reduction half-reaction will have a greater tendency to gain electrons, making it a stronger oxidizing agent.
Sample Exercise 16D:
Rank the aqueous cations Ag+, Au3+, Co2+,
and Sn2+ from weakest to strongest oxidizing agent under standard
conditions. Justify your answer using a table of standard reduction potentials.
Solution:
The cations
should be ranked from most negative to most positive E°red:
weakest oxidizing
agent = Co2+ (-0.28 V) < Sn2+ (-0.14 V) < Ag+
(+0.80 V) < Au3+ (+1.50 V) = strongest oxidizing agent
Any reduction half-reaction on the
table above can be reversed to yield an oxidation half-reaction with a standard
oxidation potential, E°ox, equal in
magnitude but opposite in sign to E°red
for the reduction half-reaction.
For example:
2 F-
(aq) → F2
(g) + 2 e-
E°ox = -2.87 V
Li (s) → Li+ (aq) + 1 e- E°ox
= +3.05 V
When E°ox
is more positive or less negative, the oxidation half-reaction will have a
greater tendency to occur. This
means that the reactant in the oxidation half-reaction will have a greater
tendency to lose electrons, making it a stronger reducing agent.
Sample Exercise 16E:
Rank the aqueous cations Co2+, Fe2+, and Sn2+ from weakest to strongest reducing agent under standard conditions. Justify your answer using a table of standard reduction potentials.
Solution:
First, we reverse the appropriate
half-reactions from the table above:
Co2+
(aq) → Co3+
(aq) + 1 e- E°ox
= -1.82 V
Fe2+
(aq) → Fe3+
(aq) + 1 e- E°ox
= -0.77 V
Sn2+
(aq) → Sn4+
(aq) + 2 e- E°ox
= -0.15 V
We then rank the cations from most negative to least negative E°ox:
weakest reducing
agent = Co2+ < Fe2+ < Sn2+ = strongest
reducing agent
Section 16-5: Calculating E°cell
and ΔG° to Determine Spontaneity of Redox Reactions
The standard cell potential (or
standard cell voltage), E°cell, for a redox reaction can be calculated by adding the standard
oxidation potential for the oxidation half-reaction to the standard reduction
potential for the reduction half-reaction:
E°cell = E°ox
+ E°red
If E°cell
is positive, the reaction will be spontaneous under standard conditions. If E°cell
is negative, the reaction will be nonspontaneous
under standard conditions.
ΔG° for a redox
reaction can be calculated from E°cell
using the following equation:
ΔG° = -nFE°cell
n represents the number of electrons
transferred in the balanced equation and is equal to the LCM of the electron
coefficients in the oxidation and reduction half-reactions prior to Step 7 of
the balancing process. F is known
as Faraday's Constant and represents
the electric charge in the unit coulombs (C) per mole of electrons. F has a value of 96,500 C/mol. Given that 1 V = 1 J/C, we will replace
the E°cell unit V with J/C when
calculating ΔG° from E°cell:
Sample Exercise 16F:
Calculate E°cell
and ΔG° for the reaction Cr (s) + Sn4+ (aq)
→ Cr3+
(aq) + Sn2+ (aq),
determine if the reaction is spontaneous or nonspontaneous
under standard conditions, and then balance the equation.
Solution:
The half-reactions prior to Step 7
of the balancing process are:
oxidation: Cr (s) → Cr3+ (aq) + 3 e- E°ox
= +0.74 V
reduction: Sn4+
(aq) + 2 e- → Sn2+ (aq) E°red
= +0.15 V
Thus, E°cell
= E°ox + E°red
= 0.74 V + 0.15 V = 0.89 V. Note
that multiplying the coefficients in each half-reaction during Step 7 of the
balancing process will not change the values of E°ox
or E°red. ΔG° can be calculated from E°cell
as follows:
n = LCM of electron coefficients 3 and 2 = 6
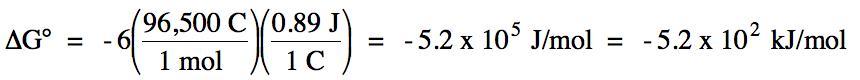
Since E°cell
> 0 and ΔG° < 0, the reaction is spontaneous under standard
conditions. The remaining steps in
the balancing process are:
oxidation: (Cr (s)
→ Cr3+
(aq) + 3 e-) x 2
reduction: (Sn4+
(aq) + 2 e- → Sn2+ (aq)) x 3
overall balanced equation: 2 Cr (s) + 3 Sn4+ (aq) → 2 Cr3+ (aq) + 3 Sn2+ (aq)
Section 16-6: Redox
Reactions of Metals, Acids, and Halogens
(a) solid metal + aqueous metal nitrate or aqueous
metal sulfate
Aqueous nitrate and sulfate ions
are generally spectator ions during redox reactions
occurring in non-acidic solutions that lack a significant concentration of H+
ions. As such, when a solid metal
reacts with an aqueous metal nitrate or metal sulfate solution, the
half-reactions follow the pattern:
oxidation: M1
(s) → M1m+
(aq) + m e-
reduction: M2n+
(aq) + n e- → M2 (s)
Therefore, the unbalanced net ionic
equation will be:
M1 (s) + M2n+ (aq) → M1m+ (aq) + M2
(s)
(b) solid metal + aqueous hydrochloric acid
HCl ionizes
completely into H+ and Cl- in
water. When a solid metal reacts
an aqueous hydrochloric acid solution, the chloride ion will be a spectator
ion. As such, the half-reactions
follow the pattern:
oxidation: M (s) → Mm+ (aq) + m e-
reduction: 2 H+
(aq) + 2 e- → H2 (g)
Therefore, the unbalanced net ionic equation will be:
M (s) + H+ (aq) → Mm+ (aq) + H2
(g)
(c) solid metal + aqueous nitric acid
HNO3 ionizes completely
into H+ and NO3- in water. When a solid metal reacts with an
aqueous nitric acid solution, since the nitrate ion is a strong oxidizing agent
in acidic solutions, the half-reactions follow the pattern:
oxidation: M (s) → Mm+ (aq) + m e-
reduction: NO3-
(aq) + 4 H+ (aq)
+ 3 e- → NO (g) + 2
H2O (l)
Therefore, the unbalanced net ionic
equation will be:
M (s) + NO3- (aq) + H+ (aq) → Mm+ (aq) + NO
(g) + H2O (l)
(d) diatomic halogen + aqueous metal halide
When a diatomic halogen reacts with
an aqueous metal halide solution, the metal ion will be a spectator ion. As such, the half-reactions will follow
the pattern:
oxidation: 2 X-
(aq) → X2
(s, l, or g) + 2 e-
reduction: Y2
(s, l, or g) + 2 e- → 2 Y-
(aq)
Therefore, the unbalanced net ionic
equation will be:
X- (aq) + Y2
(s, l, or g) → X2 (s, l, or g) + Y- (aq)
Sample Exercise 16G:
Which reaction in each pair below
will be spontaneous under standard conditions? For each spontaneous reaction, calculate E°cell
and ΔG°, then balance the equation.
1a. NiSO4
(aq) + solid manganese metal or 1b. NiSO4 (aq) + solid lead metal?
2a. aqueous
hydrochloric acid + solid magnesium metal or 2b. aqueous
hydrochloric acid + solid silver metal?
3a. aqueous
nitric acid + solid copper metal or 3b. aqueous nitric
acid + solid gold metal?
4a. liquid
bromine + aqueous potassium iodide or 4b. solid iodine
+ aqueous sodium bromide?
Solution:
1a. SO42- =
spectator ion
oxidation: Mn (s) → Mn2+
(aq) + 2 e- E°ox
= +1.18 V
reduction: Ni2+
(aq) + 2 e- → Ni (s) E°red
= -0.25 V
E°cell = 1.18 V + (-0.25 V) = 0.93 V >
0 = spontaneous
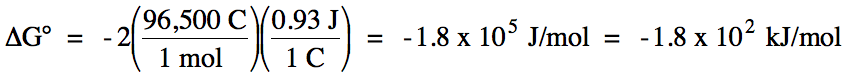
balanced equation: Mn (s) + Ni2+
(aq) → Mn2+
(aq) + Ni (s)
1b. SO42- =
spectator ion
oxidation: Pb (s) → Pb2+
(aq) + 2 e- E°ox
= +0.13 V
reduction: Ni2+
(aq) + 2 e- → Ni (s) E°red
= -0.25 V
E°cell = 0.13 V + (-0.25 V) < 0 = nonspontaneous
2a. Cl-
= spectator ion
oxidation: Mg (s) → Mg2+ (aq) + 2 e- E°ox
= +2.37 V
reduction: 2 H+
(aq) + 2 e- → H2 (g) E°red = 0 V
E°cell = 2.37 V + 0 V = 2.37 V > 0 =
spontaneous
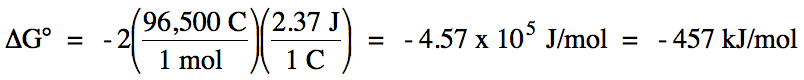
balanced equation: Mg (s) + 2 H+ (aq) → Mg2+
(aq) + H2 (g)
2b. Cl-
= spectator ion
oxidation: Ag (s) → Ag+ (aq) + 1 e- E°ox
= -0.80 V
reduction: 2 H+
(aq) + 2 e- → H2 (g) E°red
= 0 V
E°cell = (-0.80 V) + 0 V < 0 = nonspontaneous
3a.
oxidation: Cu (s) → Cu2+ (aq) + 2 e- E°ox
= -0.34 V
reduction: NO3-
(aq) + 4 H+ (aq)
+ 3 e- → NO (g) + 2
H2O (l)
E°red = +0.96 V
E°cell = (-0.34 V) + 0.96 = 0.62 V > 0
= spontaneous
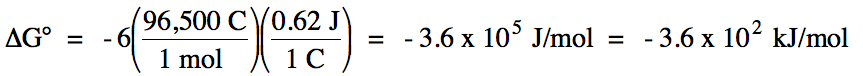
balanced equation:
3 Cu (s) + 2 NO3- (aq) +
8 H+ (aq) → 3 Cu2+ (aq) + 2 NO (g)
+ 4 H2O (l)
3b.
oxidation: Au (s) → Au3+ (aq) + 3 e- E°ox
= -1.50 V
reduction: NO3-
(aq) + 4 H+ (aq)
+ 3 e- → NO (g) + 2
H2O (l)
E°red = +0.96 V
E°cell = (-1.50 V) + 0.96 < 0 = nonspontaneous
4a. K+ = spectator ion
oxidation: 2 I-
(aq) → I2
(s) + 2 e-
E°ox = -0.53 V
reduction: Br2
(l) + 2 e- → 2 Br-
(aq) E°red
= 1.07 V
E°cell = (-0.53 V) + 1.07 = 0.54 V > 0
= spontaneous
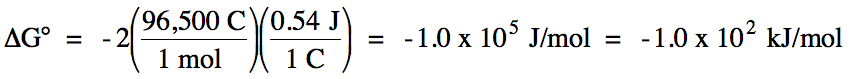
balanced equation:
2 I- (aq) + Br2 (l) → I2 (s) + 2 Br-
(aq)
4b. Na+ = spectator ion
oxidation: 2 Br-
(aq) → Br2
(l) + 2 e-
E°ox = -1.07 V
reduction: I2
(s) + 2 e- → 2 I-
(aq) E°red
= +0.53 V
E°cell = (-1.07 V) + 0.53 < 0 = nonspontaneous
Section 16-7: Experiment – Constructing a
Galvanic Cell
A galvanic cell (or voltaic cell) utilizes a spontaneous redox reaction to provide electrical energy. The oxidation and reduction
half-reactions are separated into two different compartments. As such, the electrons transferred must
flow from the location of oxidation to the location of reduction through a
metal wire. This spontaneous
movement of electrons provides electrical energy.
A galvanic cell can be constructed
using standard laboratory chemicals and equipment as follows:
1. Immerse one end of a metal strip
in a beaker containing aqueous ions of that same metal. Repeat in a second beaker using a
different metal. Note that the
anions in each beaker will be spectator ions.
2. Connect the non-immersed ends of
the two metal strips using a metal wire.
A voltmeter can be attached along the wire to read the voltage as the
galvanic cell operates. Note that
if 1 M aqueous solutions are used in the beakers, then the reading on the
voltmeter will be equal to E°cell for the
spontaneous reaction.
3. Connect the aqueous solutions in
the two beakers using a salt bridge that can be constructed using a U-shaped
glass tube containing an aqueous ionic salt. Note that the ions in the salt bridge will not be part of
the spontaneous reaction. The
purpose of the salt bridge is to keep the solutions in each beaker electrically
neutral, which means that the total positive charge equals the total negative
charge. Negatively-charge anions
will flow out from the salt bridge into the beaker where oxidation is occurring
to counteract the positively-charged metal cations being created there. Positively-charged cations will flow out from the salt bridge into the beaker
where reduction is occurring to replace the positively-charged metal cations being consumed there.
A sketch of a galvanic cell in
operation is shown below:
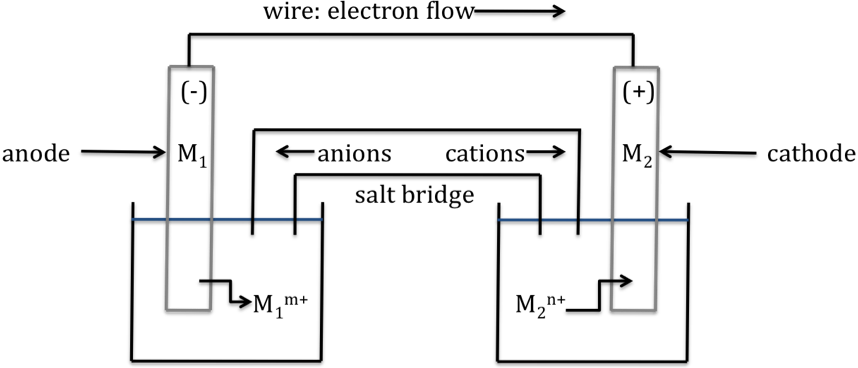
Key aspects of the galvanic cell
are:
1. The metal electrode that
undergoes oxidation (M1) is known as the anode and is typically labeled (-). The anode will lose mass as the reaction proceeds. The metal electrode that is the product
of reduction (M2) is known as the cathode and is typically labeled (+). The cathode will gain mass as the reaction proceeds.
2. Electrons flow through the wire
from anode to cathode, or from (-) to (+).
3. Anions flow out of the salt
bridge toward the anode. Cations flow out of the salt bridge toward the
cathode.
Sample Exercise 16H:
A galvanic cell was constructed
using a strip of aluminum metal and a strip of zinc metal, a 1 M solution of Al(NO3)3 and a 1 M solution of ZnSO4,
and an aqueous solution of KNO3 in the salt bridge. For the spontaneous reaction that
occurred, calculate E°cell and ΔG°, then
balance the equation. Also sketch
the galvanic cell.
Solution:
We must choose the correct
combination of half-reactions to obtain a spontaneous reaction (nitrate and
sulfate = spectator ions):
oxidation: Al (s) → Al3+ (aq) + 3 e- E°ox
= +1.66 V
reduction: Zn2+
(aq) + 2 e- → Zn (s) E°red
= -0.76 V
E°cell = 1.66 V + (-0.76 V) = 0.90 V >
0 = spontaneous
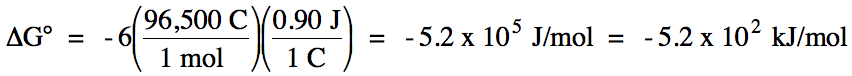
balanced equation: 2 Al (s) + 3 Zn2+ (aq) → 2 Al3+
(aq) + 3 Zn (s)
Redraw the galvanic cell sketch shown
above, making the following substitutions:
M1
= Al, M1m+ = Al3+
M2
= Zn, M2n+ = Zn2+
anions = NO3-, cations
= K+
Section 16-8: Nonspontaneous
Redox Reactions and Electrolysis
A nonspontaneous
redox reaction can still occur through a process
known as electrolysis if a high
enough voltage is applied. As is the case for a galvanic cell, oxidation occurs at the anode and reduction occurs at the cathode in an electrolytic cell. The
minimum voltage required for electrolysis under standard conditions is equal to
the absolute value of E°cell for the nonspontaneous reaction:
electrolysis: minimum
voltage = |E°cell|
Sample Exercise 16I:
Calculate the minimum voltage
required to bring about the reaction Br- (aq)
+ Fe3+ (aq) →Br2 (l) + Fe2+ (aq)
by electrolysis under standard conditions, then balance the equation.
Solution:
oxidation (at anode): 2 Br-
(aq) → Br2
(l) + 2 e-
E°ox = -1.07 V
reduction (at cathode): Fe3+
(aq) + 1 e- → Fe2+ (aq) E°red
= +0.77 V
E°cell = (-1.07 V) + 0.77 = -0.30 V
minimum voltage = |-0.30 V| = 0.30 V
balanced equation:
2 Br- (aq) + 2 Fe3+ (aq) → Br2
(l) + 2 Fe2+ (aq)
If a liquid (also known as molten)
ionic metal halide such as LiCl, CaBr2, or NaI is
electrolyzed, the halide anion will be oxidized at the anode to a neutral
diatomic halogen while the metal cation will be reduced at the cathode to a
neutral metal:
oxidation (at
anode): 2 X -→ X2 + 2 e-
reduction (at
cathode): Mn+ + n e- → M
Sample Exercise 16J:
For the electrolysis of molten LiCl,
write the half-reaction that occurs at the anode and the half-reaction that
occurs at the cathode, then balance the equation.
Solution:
oxidation (at
anode): 2 Cl- → Cl2 + 2 e-
reduction (at
cathode): Li+ + 1 e- → Li
balanced
equation: 2 Cl- + 2 Li+ → Cl2 + 2Li
The total charge in coulombs (C)
transferred during electrolysis can be found by multiplying the time of
electrolysis in seconds by the current in amperes (A), where 1 A = 1 C/s:
(time in s)
x (current in C/s) = charge in C
Once we know the total charge
transferred in C, we can divide by F = 96,500 C/mol e- to find the
total moles of electrons transferred during electrolysis. From the total moles of electrons
transferred, we can use the mole ratio from the relevant half-reaction to find
the moles of a product of interest, after which moles of product can be
converted to any desired unit.
Starting with time, the general
strategy employed in order to determine the quantity of a product formed during
electrolysis is as follows:
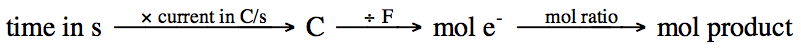
Starting with the quantity of
product, the general strategy employed in order to determine the time of
electrolysis is as follows:
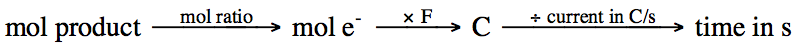
We will use dimensional analysis to
implement each strategy above as follows:
Sample Exercise 16K:
For the electrolysis of molten LiCl:
a. If the electrolyis proceeds for
244 minutes using a current of 0.485 A, how many milliliters of Cl2 gas, measured at 35°C and 711 mmHg, will be produced?
b. Using a current of 1.8 A, how
many hours must the electrolysis proceed to produce 1.3 g of Li?
Solution:
a. The relevant half-reaction is:
oxidation
(at anode): 2 Cl- → Cl2 + 2 e-
b. The relevant half-reaction is:
reduction
(at cathode): Li+ + 1 e- → Li
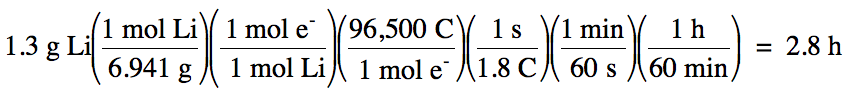
Chapter 16 Practice Exercises and Review Quizzes:
16-1) Determine
all oxidation numbers in:
a. Ga3+
b. S2O32-
c. Br2
d. H2O2
e. CaH2
Click for Solution
16-1)
a. Ga =
+3 (Rule 3)
b. Conflict: Rule 5e (O = -2) takes priority over
Rule 5g
2(S) + 3(-2) = -2
S = +2
c. Br = 0 (Rule 2)
d. Conflict: Rule 5c (H = +1) takes priority over Rule
5e
2(+1) + 2(O) = 0
O = -1
e. Conflict: Rule 5b (Ca = +2) takes priority over
Rule 5c
(+2) + 2(H) = 0
H = -1
16-2) Determine
all oxidation numbers in the following unbalanced reactions, and then decide
which of the two is a redox reaction. For the redox
reaction, identify the reducing agent and the oxidizing agent.
a. ClO4- + Ge2+
→ ClO3- + Ge4+
b. Mg(NO3)2
+ KOH → Mg(OH)2
+ KNO3
Click for Solution
16-2) Using oxidation number rules
in order of priority:
a. ClO4- (O =
-2, Cl = +7) + Ge2+ (Ge
= +2) → ClO3- (O = -2, Cl = + 5) + Ge4+ (Ge =
+4)
Since oxidation numbers change,
this is a redox reaction. Ge2+ contains the element Ge
that undergoes an increase in oxidation number from +2 to +4, so Ge2+
is the reducing agent. ClO4-
contains the element Cl that undergoes a decrease in
oxidation number from +7 to +5, so ClO4- is the oxidizing
agent.
b. Mg(NO3)2
(Mg = +2, O = -2, N = +5) + KOH (K = +1, H = +1, O = -2) → Mg(OH)2 (Mg = +2, H =
+1, O = -2) + KNO3 (K = +1, O = -2, N = +5)
Since no elements undergo a change
in oxidation number, this is not a redox reaction.
16-3) Determine all oxidation
numbers, identify the reducing agent and oxidizing agent, and balance the
following equation that occurs in aqueous acidic solution using the smallest
possible whole-number coefficients:
MnO4-
+ As2O3 → Mn2+
+ H3AsO4
Click for Solution
16-3)
Step 1:
MnO4-
(O = -2, Mn = +7) + As2O3 (O =
-2, As = +3) → Mn2+
(Mn = +2) + H3AsO4 (H = +1, O =
-2, As = +5)
reducing agent = As2O3 (oxidation number
of As increases from +3 to +5)
oxidizing agent = MnO4- (oxidation number
of Mn decreases from +7 to +2)
Step 2:
oxidation: As2O3
→ H3AsO4
reduction: MnO4-
→ Mn2+
Step 3:
oxidation: As2O3
→ 2 H3AsO4
reduction: MnO4-
→ Mn2+
Step 4:
oxidation: As2O3
+ 5 H2O → 2 H3AsO4
reduction: MnO4-
→ Mn2+
+ 4 H2O
Step 5:
oxidation: As2O3
+ 5 H2O → 2 H3AsO4
+ 4 H+
reduction: MnO4-
+ 8 H+ → Mn2+
+ 4 H2O
Step 6:
oxidation: As2O3
+ 5 H2O → 2 H3AsO4
+ 4 H+ + 4 e-
reduction: MnO4-
+ 8 H+ + 5 e- → Mn2+
+ 4 H2O
Step 7: LCM of electron coefficients 4 and 5 = 20
oxidation: (As2O3
+ 5 H2O → 2 H3AsO4
+ 4 H+ + 4 e-) x 5
= 5 As2O3
+ 25 H2O → 10 H3AsO4
+ 20 H+ + 20 e-
reduction: (MnO4-
+ 8 H+ + 5 e- → Mn2+
+ 4 H2O) x 4
= 4 MnO4-
+ 32 H+ + 20 e- → 4 Mn2+
+ 16 H2O
Step 8:
5 As2O3
+ 25 H2O + 4 MnO4- + 32 H+ + 20 e-
→ 10 H3AsO4
+ 20 H+ + 20 e- + 4 Mn2+ + 16 H2O
overall balanced equation: 5 As2O3 + 9
H2O + 4 MnO4- + 12 H+ → 10 H3AsO4 +
4 Mn2+
(total charge on left = 5 x 0 + 9 x 0 + 4 x -1 + 12 x 1 = +8,
total charge on right = 10 x 0 + 4 x 2 = +8)
16-4) Rank the halogens Br2 (l), Cl2
(g), F2 (g), and I2
(s) from weakest to strongest oxidizing agent under standard conditions.
Justify your answer using a table of standard reduction potentials.
Click for Solution
16-4) The
halogens should be ranked from least positive to most positive E°red:
weakest oxidizing
agent = I2 (+0.53 V) < Br2 (+1.07 V) < Cl2
(+1.36 V) < F2 (+2.87 V) = strongest oxidizing agent
16-5) Rank the solid alkaline earth metals Ba, Ca, and Mg from weakest to strongest reducing agent under standard conditions. Justify your answer using a table of standard reduction potentials.
Click for Solution
16-5) First, we reverse the
appropriate half-reactions from the table of standard reduction potentials:
Mg (s) → Mg2+ (aq) + 2 e- E°ox
= +2.37 V
Ca (s) → Ca2+ (aq) + 2 e- E°ox
= +2.87 V
Ba (s) → Ba2+
(aq) + 2 e- E°ox
= +2.90 V
We then rank the metals from least
positive to most positive E°ox:
weakest reducing
agent = Mg < Ca < Ba = strongest reducing agent
16-6) Calculate E°cell and
ΔG° for the reaction V3+ (aq) + I- (aq) → V2+ (aq) + I2 (s), determine if the reaction is spontaneous or nonspontaneous under standard
conditions, and then balance the equation.
Click for Solution
oxidation: 2 I- (aq) → I2 (s) + 2 e- E°ox =
-0.53 V
reduction: V3+ (aq) + 1 e-→ V2+ (aq) E°red =
-0.26 V
Thus, E°cell = E°ox + E°red = (-0.53 V) + (-0.26 V) = -0.79 V. Note that multiplying the coefficients in each half-reaction
during Step 7 of the balancing process will not change the values of E°ox or E°red. ΔG° can be
calculated from E°cell as follows:
n = LCM of
electron coefficients 2 and 1 = 2
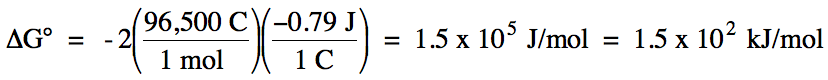
Since E°cell < 0 and
ΔG° > 0, the reaction is nonspontaneous under standard conditions. The remaining steps in the balancing
process are:
oxidation: (2 I- (aq) → I2 (s) + 2 e-)
x 1
reduction: (V3+ (aq) + 1 e-→ V2+ (aq)) x 2
overall balanced equation: 2 V3+ (aq) + 2 I- (aq) → 2 V2+ (aq) + I2 (s)
16-7) Which
reaction in each pair below will be spontaneous under standard conditions? For each spontaneous reaction,
calculate E°cell and ΔG°, then balance the
equation.
1a. aqueous
nitric acid + solid gold metal or 1b. aqueous nitric
acid + solid silver metal?
2a. liquid bromine + aqueous potassium chloride or 2b. chlorine gas + aqueous sodium iodide?
3a. AgNO3
(aq) + solid copper metal or 3b. AgNO3 (aq) + solid gold metal?
4a. aqueous
hydrochloric acid + solid copper metal or 4b. aqueous
hydrochloric acid + solid zinc metal?
Click for Solution
16-7)
1a.
oxidation: Au (s) → Au3+ (aq) + 3 e- E°ox
= -1.50 V
reduction: NO3-
(aq) + 4 H+ (aq)
+ 3 e- → NO (g) + 2
H2O (l)
E°red = +0.96 V
E°cell = (-1.50 V) + 0.96 < 0 = nonspontaneous
1b.
oxidation: Ag (s) → Ag+ (aq) + 1 e- E°ox
= -0.80 V
reduction: NO3-
(aq) + 4 H+ (aq)
+ 3 e- → NO (g) + 2
H2O (l)
E°red = +0.96 V
E°cell = (-0.80 V) + 0.96 = 0.16 V > 0
= spontaneous
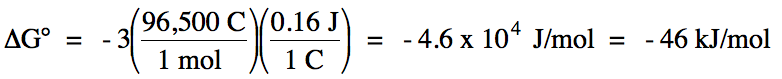
balanced equation:
3 Ag (s) + NO3- (aq) + 4
H+ (aq) → 3 Ag+ (aq) + NO (g) + 2
H2O (l)
2a. K+ = spectator ion
oxidation: 2 Cl- (aq) → Cl2 (g) + 2 e- E°ox
= -1.36 V
reduction: Br2
(l) + 2 e- → 2 Br-
(aq) E°red
= 1.07 V
E°cell = (-1.36 V) + 1.07 < 0 = nonspontaneous
2b. Na+ = spectator ion
oxidation: 2 I-
(aq) → I2
(s) + 2 e-
E°ox = -0.53 V
reduction: Cl2
(g) + 2 e- → 2 Cl- (aq) E°red
= +1.36 V
E°cell = (-0.53 V) + 1.36 = 0.83 V > 0
= spontaneous
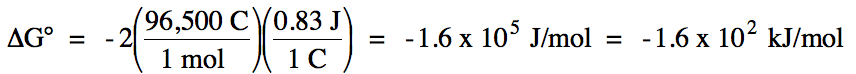
balanced equation:
2 I- (aq) + Cl2 (g) → I2 (s) + 2 Cl- (aq)
3a. NO3- =
spectator ion
oxidation: Cu (s) → Cu2+ (aq) + 2 e- E°ox
= -0.34 V
reduction: Ag+
(aq) + 1 e- → Ag (s) E°red
= +0.80 V
E°cell = (-0.34 V) + 0.80 V = 0.46 V >
0 = spontaneous
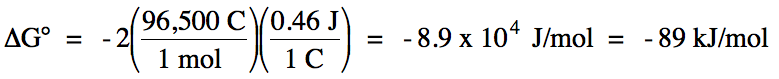
balanced equation: Cu (s) + 2 Ag+ (aq) → Cu2+
(aq) + 2 Ag (s)
3b. NO3- =
spectator ion
oxidation: Au (s) → Au3+ (aq) + 3 e- E°ox
= -1.50 V
reduction: Ag+
(aq) + 1 e- → Ag (s) E°red
= +0.80 V
E°cell = (-1.50 V) + 0.80 < 0 = nonspontaneous
4b. Cl-
= spectator ion
oxidation: Cu (s) → Cu2+ (aq) + 2 e- E°ox
= -0.34 V
reduction: 2 H+
(aq) + 2 e- → H2 (g) E°red
= 0 V
E°cell = (-0.34 V) + 0 V < 0 = nonspontaneous
4a. Cl-
= spectator ion
oxidation: Zn (s) → Zn2+ (aq) + 2 e- E°ox
= +0.76 V
reduction: 2 H+
(aq) + 2 e- → H2 (g) E°red
= 0 V
E°cell = 0.76 V + 0 V = 0.76 V > 0 =
spontaneous
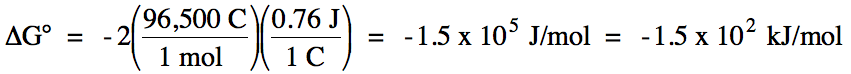
balanced equation: Zn (s) + 2 H+ (aq) → Zn2+
(aq) + H2 (g)
16-8) A galvanic cell was
constructed using a strip of cadmium metal and a strip of chromium metal, a 1 M
solution of CdSO4 and a 1 M solution of Cr(NO3)3,
and an aqueous solution of Na2SO4 in the salt
bridge. For the spontaneous
reaction that occurred, calculate E°cell
and ΔG°, then balance the equation.
Also sketch the galvanic cell.
Click for Solution
16-8) We
must choose the correct combination of half-reactions to obtain a spontaneous
reaction (nitrate and sulfate = spectator ions):
oxidation: Cr (s) → Cr3+ (aq) + 3 e- E°ox
= +0.74 V
reduction: Cd2+
(aq) + 2 e- → Cd (s) E°red
= -0.40 V
E°cell = 0.74 V + (-0.40 V) = 0.34 V >
0 = spontaneous
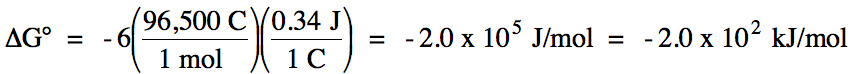
balanced equation: 2 Cr (s) + 3 Cd2+ (aq) → 2 Cr3+
(aq) + 3 Cd (s)
Redraw the galvanic cell sketch shown
above, making the following substitutions:
M1
= Cr, M1m+ = Cr3+
M2
= Cd, M2n+ = Cd2+
anions = SO42-, cations
= Na+
16-9) Calculate the minimum voltage
required to bring about the reaction Ag (s) + Sn4+ (aq) → Ag+
(aq) + Sn2+ (aq)
by electrolysis under standard conditions, then balance the equation.
Click for Solution
16-9)
oxidation (at anode): Ag (s) → Ag+ (aq) + 1 e- E°ox
= -0.80 V
reduction (at cathode): Sn4+
(aq) + 2 e- → Sn2+ (aq) E°red
= +0.15 V
E°cell = (-0.80 V) + 0.15 = -0.65 V
minimum voltage = |-0.65 V| = 0.65 V
balanced equation:
2 Ag (s) + Sn4+ (aq) → 2 Ag+ (aq) + Sn2+ (aq)
16-10) For the electrolysis of
molten CaBr2, write the half-reaction that occurs at the anode and
the half-reaction that occurs at the cathode, then balance the equation.
Click for Solution
oxidation (at
anode): 2 Br- → Br2 + 2 e-
reduction (at
cathode): Ca2+ + 2 e- → Ca
balanced equation: 2 Br- + Ca2+ → Br2 + Ca
16-11) For the electrolysis of
molten CaBr2:
a. If the electrolyis proceeds for 2.0
hours using a current of 3.4 A, how many grams of Ca will be produced?
b. Using a current of 0.925 A, how
many minutes must the electrolysis proceed to produce 1.55 x 1022 Br2 molecules?
Click for Solution
a. The relevant half-reaction is:
reduction
(at cathode): Ca2+ + 2
e- → Ca
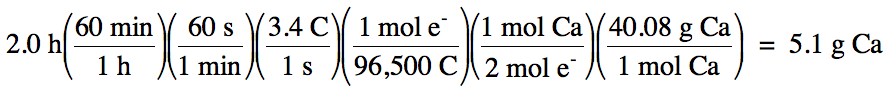
b. The relevant half-reaction is:
oxidation
(at anode): 2 Br- → Br2 + 2 e-
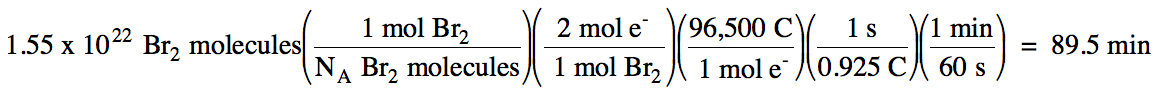
Click for Review Quiz 1 Answers